Понятие марковского случайного процесса
Финальные вероятности и граф состояний СМО
Основные понятия имитационного моделирования
Граф состояний системы и уравнения Колмогорова
Расчет показатели эффективности системы по финальным вероятностям
Блок-схема программы
Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
Навигация
Расчет показатели эффективности системы по финальным вероятностям
Имитационное моделирование системы массового обслуживания
48014
знаков
3
таблицы
9
изображений
2.3 Расчет показатели эффективности системы по финальным вероятностям
Найдем показатели эффективности системы массового обслуживания. Наиболее важными являются следующие показатели:
1) Вероятность отказа в обслуживании заявки, т.е. вероятность того, что заявка покидает систему не обслуженной. В нашем случае заявке отказывается в обслуживании, если все 4 канала заняты, и очередь максимально заполнена (т.е. 3 человека в очереди), это соответствует состоянию системы S7. Т.к. вероятность прихода системы в состояние S7 равна Р7 , то
2) Относительная пропускная способность – это средняя доля поступивших заявок, обслуживаемых системой.
3) Абсолютная пропускная способность – это среднее число заявок, обслуживаемых в единицу времени.
4) Длина очереди, т.е. среднее число заявок в очереди. Длина очереди равна сумме произведений числа человек в очереди на вероятность соответствующего состояния.
5) Среднее время пребывания заявки в очереди определяется формулой Литтла
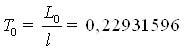
6) Среднее число занятых каналов определяется следующим образом:
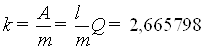
Глава 3. Имитационное моделирование СМО
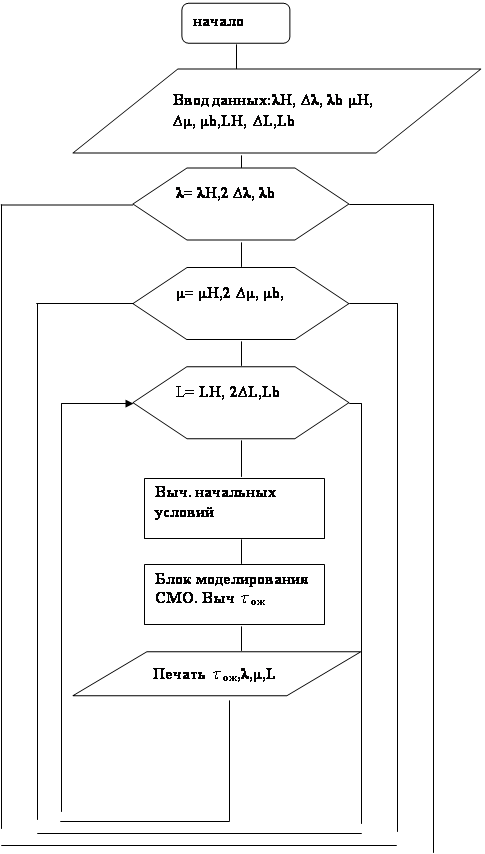
3.1 Алгоритм метода имитационного моделирования СМО (пошаговый подход)
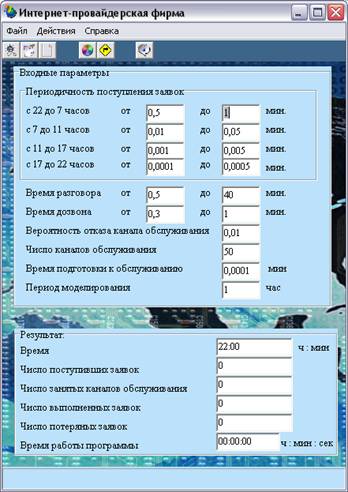
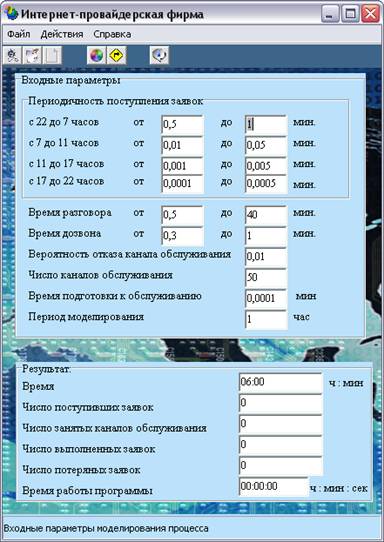
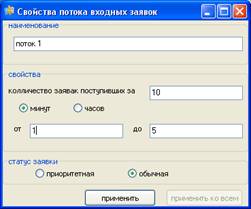
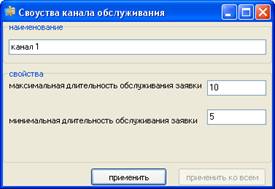
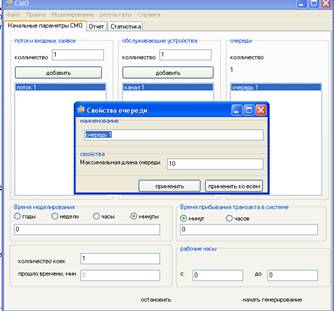
Рассмотрим четырехканальную систему массового обслуживания (n = 3) с максимальной длиной очереди равной четырем (m = 2). В СМО поступает простейший поток заявок со средней интенсивностью λ = 4 и показательным законом распределения времени между поступлением заявок. Поток обслуживаемых в системе заявок является простейшим со средней интенсивностью μ = 1 и показательным законом распределения временем обслуживания.
Для имитации СМО воспользуемся одним из методов статистического моделирования – имитационным моделированием. Будем использовать пошаговый подход. Суть этого подхода в том, что состояния системы рассматриваются в последующие моменты времени, шаг между которыми является достаточно малым, чтобы за его время произошло не более одного события.
Выберем шаг по времени (
). Он должен быть много меньше среднего времени поступления заявки (
) и среднего времени ее обслуживания (
), т.е.
, где (3.1.1)
Исходя из условия (3.1.1) определим шаг по времени 
.
Время поступления заявки в СМО и время ее обслуживания являются случайными величинами. Поэтому, при имитационном моделировании СМО их вычисление производится с помощью случайных чисел.
Рассмотрим поступление заявки в СМО. Вероятность того, что на интервале в СМО поступит заявка, равна:
.
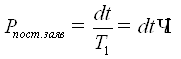Сгенерируем случайное число 
, и, если 
, то будем считать, что заявка на данном шаге в систему поступила, если 
, то не поступила.
В программе это осуществляет функция 
. Интервал времени примем постоянным и равным 0,001, тогда отношение 
будет равно 1000 . Если заявка поступила, то она принимает значение «истина», в противном случае значение «ложь».
function sob: boolean;
var r:real;
begin
r := Random(1000)/1000;
if r <= (i_deltaT*r_Lamda) then
sob:= true
else
sob:= false;
end;
Рассмотрим теперь обслуживание заявки в СМО. Время обслуживания заявки в системе определяется выражением
,
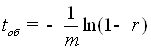где 
– случайное число. В программе время обслуживания определяется с помощью функции 
.
function tok: real;
var r:real;
t_ob: real;
begin
r:= Random(1000)/1000;
t_ob:= -1/r_Mu*ln(1-r);
tok:= t_ob;
end;
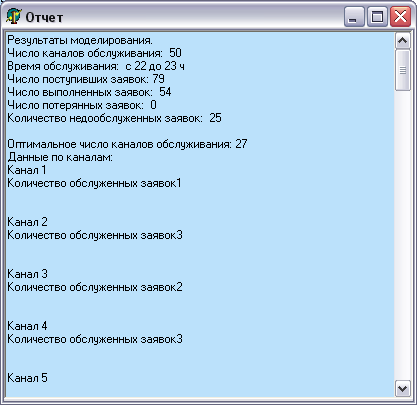
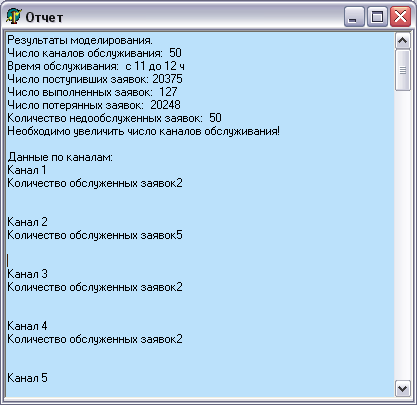
Алгоритм метода имитационного моделирования можно сформулировать следующим образом. Время работы СМО (Т) разбивается на шаги по времени dt, на каждом из них выполняется ряд действий. Вначале определяются состояния системы (занятость каналов, длина очереди), затем, с помощью функции , определяется, поступила ли на данном шаге заявка или нет.
Если поступила, и, при этом имеются свободные каналы, то с помощью функции генерируем время обработки заявки и ставим ее на обслуживание. Если все каналы заняты, а длина очереди меньше 4, то помещаем заявку в очередь, если же длина очереди равна 4, то заявке будет отказано в обслуживании.
В случае, когда на данном шаге заявка не поступала, а канал обслуживания освободился, проверяем, есть ли очередь. Если есть, то из очереди заявку ставим на обслуживание в свободный канал. После проделанных операций время обслуживания для занятых каналов уменьшаем на величину шага dt. По истечении времени Т, т.е., после моделирования работы СМО, вычисляются показатели эффективности работы системы и результаты выводятся на экран.
Похожие работы
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
... (с 17 до 22 часов)время суток. Следовательно при одном и том же количестве каналов обслуживания, в ночное время вероятность занятости канала будет меньше, чем в дневное. Особенностью этой модели системы массового обслуживания является отсутствие очереди. Если в момент совершения заявки свободных каналов не оказалось, то она покидает систему: то есть если клиент не дозванивается, то и факт ...
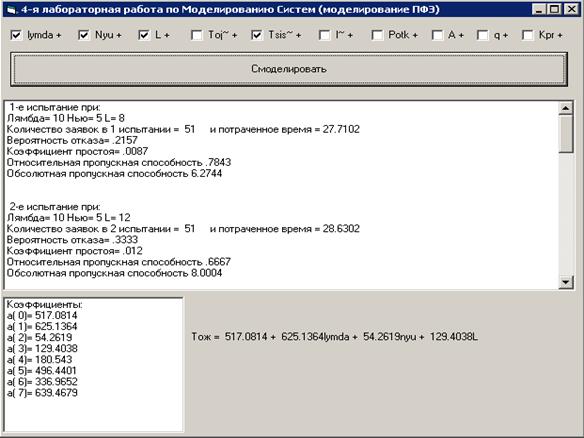
... лабораторной работе, входит: 1. Анализ зависимости влияния экзогенных переменных модели однофазной одноканальной СМО на эндогенные переменные. 2. Построение плана машинного эксперимента на основе множественного регрессионного анализа и метода наименьших квадратов. 3.Моделирование системы массового обслуживания В качестве объекта моделирования рассматривается однофазная одноканальная система, ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
0 комментариев