Анализ способов повышения надежности и долговечности работы манжетных уплотнений валов автомобилей
Экспериментальные исследования процесса обработки выглаживанием широким самоустанавливающимся инструментом
Далее для упрощения расчета произвести развертку цилиндрической поверхности так, как показано на рис. 4.1.б;
Алгоритм решения систем нелинейных уравнений численным методом
Выбор необходимого решения из решений полученных на этпах. 5.1. и 5.2. путем отыскания из них решения с наименьшим значением y
Анализ результатов математического моделирования
Определение затрат на НИР (предпроизводственных затрат)
Расчет экономического эффекта от реализации проекта
Навигация
Алгоритм решения систем нелинейных уравнений численным методом
Повышение надежности и долговечности работы манжетных уплотнений валов автомобилей ВАЗ
106261
знак
13
таблиц
35
изображений
4.1.1 Алгоритм решения систем нелинейных уравнений численным методом
В повседневной жизни мы часто сталкиваемся со всякого рода колебательными процессами. При составлении их математических моделей в целях упрощения используется уравнение гармонических колебаний вида: y = S+Asin(w t +j) или y = S+Acos(w t +j). Система, описанная одним из этих уравнений, может находиться во взаимодействии с другой системой, но при этом даже если система описана линейным уравнением вида: y = k x+b, – возникают сложности при решении систем уравнений:
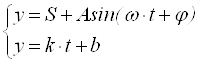
Существует множество различных пакетов прикладных программ, предназначенных для проведения математических и научно-технических расчетов. Прежде всего к ним следует отнести такие программы как Mathematica, MatLab, Maple, MathCad и др., но каждая из этих программ при решении систем нелинейных уравнений использует уже введенный разработчиками алгоритм, который сводится к использованию метода итерации, то есть нахождению решения с помощью последовательного приближения. Но такие встроенные алгоритмы универсальны и рассчитаны прежде всего на большой спектр разновидностей систем уравнений, носящих как линейный так и нелинейный характер, что замедляет их быстродействие и затрудняет их применение при громоздких циклических вычислениях. К недостатку также можно отнести и тот факт, что данные алгоритмы не всегда дают достоверный ответ, из-за универсальности их практически невозможно применять в некоторых частных случаях, о чем свидетельствует ряд проделанных расчетов в MathCad и MatLab.
В случае достаточно громоздких вычислений такая процедура занимает относительно много времени. Поэтому был разработан специальный алгоритм, позволяющий находить решение системы нелинейных уравнений с заданной точностью. Суть расчета заключается в постепенном приближении к истинному значению у методом итерации при изменении времени t. Структура данного алгоритма состоит из следующих этапов:
1. Определение значения параметра t уравнения, с которого начинается итерация (tнач=–b/k, с) и области определения решения системы уравнения:
tлев = (S-A-b)/k-1/(20×w), с;
tправ = (S+A-b)/k+1/(20×w), с (см. рис. 4.9).
Значение равное 1/(20×w) (первоначальный шаг итерации) добавлено для расширения границ области поиска решения.
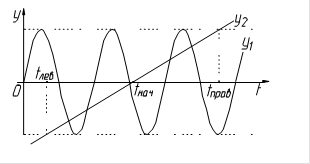
Рис. 4.9. Пояснительная схема к первому этапу итерации
3. Расчет вспомогательного коэффициента K при проверки выполнения условия: у1(tнач)>у2(tнач), см. рис. 4.10.
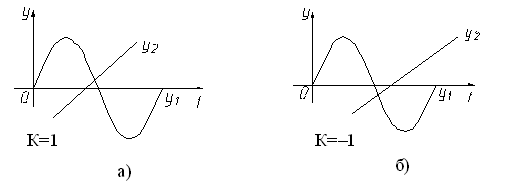
Рис. 4.10. Пояснительная схема к определению вспомогательного коэффициента К
4. Расчет начальной разности значений: ïу1(tнач)–у2(tнач)ï.
4. Определение первоначального шага итерации (dt=1/(20w)) и приравнивание к текущему значению параметра t=tнач.
5. Нахождение значения у методом итерации в двух направлениях:
5.1. Проведение итерации в направлении оси абсцисс (см. рис. 4.11): идет приращение параметра t=t+dt (первоначально t=tнач).
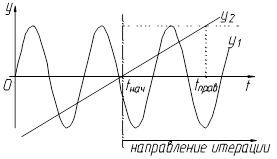
Рис. 4.11. Итерация в направлении оси абсцисс
Как видно из рис. 4.12 при первоначальном значении времени t не выполняется условие y2>y1, то есть K=1. Приращение к параметру t идет до тех пор, пока не выполнится условие К×(y1–y2)<0, что означает переход через точку пересечения графиков. Далее совершаются следующие операции: t=t-dt, dt=dt/2 и проверяется условие: 
, где Dy – точность расчета корней. Если последнее условие выполняется итерация прекращается и запоминается временное значение yврем1=y2 и tврем1 = t, в противном случае итерация продолжается с измененным значением dt (см. рис. 4.12). При этом необходимо следить чтобы значение параметра t не вышло за пределы [tлев, tправ].
Рис. 4.12. Порядок проведения итерации
5.2. Проведение итерации в противоположном направлении оси абсцисс (см. рис. 4.13): идет уменьшение параметра t=t-dt (первоначально t=tнач). При этом совершаются действия аналогичные, описанным на этапе 5.1. для отыскания решения системы уравнений.
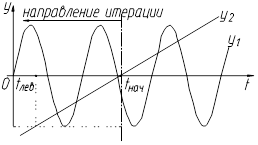
Рис. 4.13. Итерация в противоположном направлении оси абсцисс
Похожие работы
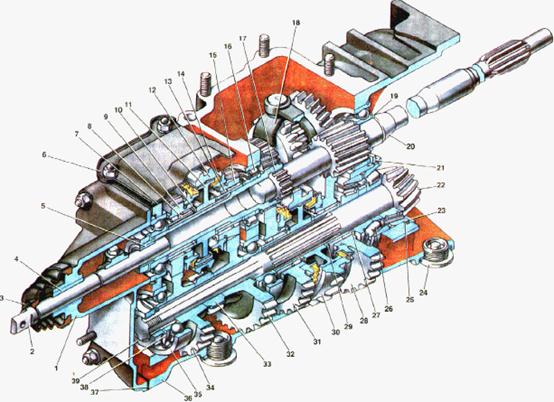
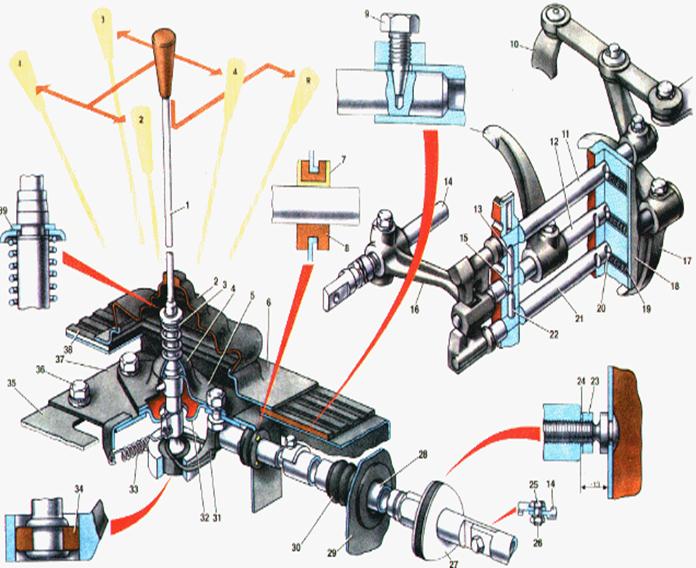
... хода зубчатое колесо 3 передвигают назад, вводя его в зацепление с промежуточным зубчатым колесом 5 передачи заднего хода, свободно вращающимся на своей оси. Общее устройство коробки передач На различных автомобилях устройство коробки передач может отличаться, но принципиальная схема остаётся примерно одинаковой. В этом разделе мы рассмотрим общее её устройство. Коробка передач (рис. 1) ...
... -12рк (ТУ 38.101844-80). ТАД-17И (класс 18) получают смешением остаточного и дистиллятного масел с введением многофункциональной и депрессорной присадок. Масло обладает высокими эксплуатационными свойствами, является универсальным и может применяться в тяжелонагруженных цилиндрических, спирально-конических и гипоидных передачах грузовых и легковых автомобилей в умеренной и жаркой климатических ...
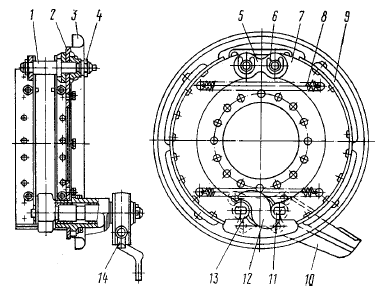
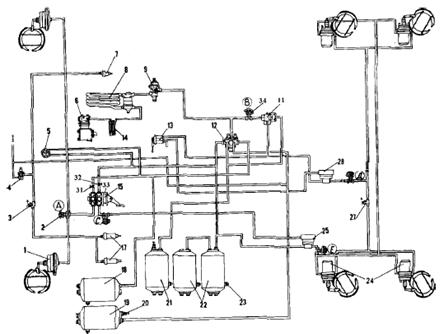
... колодка тормозная; 8 – пружина; 9 – накладка фрикционная; 10-кронштейн разжимного кулака; 11 – ось ролика; 12 – кулак разжимной; 13 – ролик; 14 – рычаг регулировочный 1.2 Устройство тормозной системы с пневматическим приводом Устройство тормозной системы показано на рис. 1.2. Источником сжатого воздуха в приводе является компрессор 9. Компрессор, регулятор давления 11, предохранитель 12 от ...
0 комментариев