Рассчитаем положение нейтрали

2.4 Рассчитаем положение нейтрали

L_I=,

где l_k – длина обмотки, l_k =0,05 м.

L_I=5 м.

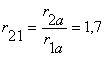- перевод в базисные величины.

Функции для расчета коэффициентов уравнения для определения нейтрали:

,

,

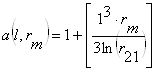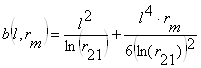где r_m – магнитное сопротивление.

Напряженность в относительной форме:

A/м,

где α, β,γ – коэффициенты аппроксимации; α=625; β=19,5; γ=44,5.

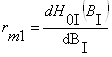; r_m1=2,822*10 ^–3 Гн ^–1.

B₁=B_I – индукция не насыщенной «стали 3»;

B_c=2 Тл – индукция потоков рассеяния;

B₂=1,75 Тл – индукция насыщенной «стали3»;

Ф_с=r_с²*В_с – поток рассеяния;

r_m1 – магнитное сопротивление не насыщенной «стали3»:

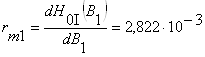Гн ^–1;

r_m2 – магнитное сопротивление насыщенной «стали3»:

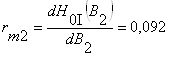 Гн ^–1.

Коэффициент, входящий в уравнение нейтрали:

.

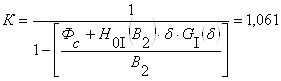Рассчитаем положение нейтрали для рабочего зазора δ=0,015 м.

=0,01 м.; l₂=0,02 м.; l₃=0,02 м.

Определим магнитные потоки:

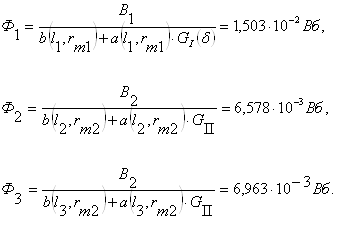
Результирующий поток:

Удельное МДС:

 f _I=6,963*10 ^–3 A/м.

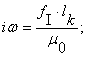 iω=2,77*10 ⁴ A/витков.

Рассчитаем число витков обмотки:

Выбираем [1] если импульсы питания короткие и частота небольшая f ≤ 2 Гц.

Е _I=0,1

Е=27 В-напряжение питания.

Число витков обмотки:

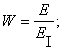 W=270 витков.

Ток обмотки в коротком импульсе:

 i=20A.

Сечение окна обмотки:

r_1а=0,01 м.,

r_2а=0,0125 м.,

перевод в метры,

Коэффициент заполнения обмотки: k_z=0,4

Сечение меди: S_мед=k_z*S; S_мед=50.24 мм.

Сечение провода: .

Диаметр провода: 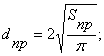 d_пр=0,48 мм.

Округляем до ближайшего большего числа и получаем: d_пр=0.5 мм.

Длина провода, выраженная через радиус витка:

; l_пр=19.07 м.

Сечение, выраженное через средний радиус витка:

.

Сопротивление обмотки: ,

ρ=0,01 Ом – удельное сопротивление провода обмотки (справочные данные).

R=2.1*10 ^–5 Ом.

Расчет коэффициентов для уравнения динамики ЛЭМД:

δ=0,015 м. – начальный рабочий зазор.

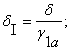 δ _I=1,5 – перевод в относительную форму.

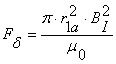- базисное значение силы тяги; F_δ=2,5*10 ² Н.

Тяговое усилие от притяжения в рабочем зазоре:

,

Тяговое усилие от потоков рассеяния:

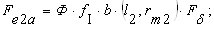
F_е2a=0,145 H.

Полное тяговое усилие, в исходном положении якоря:

 F_la=275,145H.

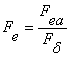- приведенное значение.

Якорь располагается эксцентрично в круглом отверстии фланца, в следствие чего возникает сила одностороннего магнитного притяжения, вызывающая трение между направляющим стержнем и фланцем; найдем ее:

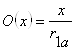 – функция преобразования абсолютного значения в относительное.

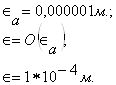
Величина нерабочего зазора Δа=0,0002 м.

Δ=О(Δa); Δ=0.002 м.

Толщина фланца h_na=0,005 м.

h_n=O(h_na); h_n=0,5 мм.

Коэффициент трения якоря о втулку k=0,022.

Индукция направляющего стержня: В_с=2 Тл.

Радиус стержня: r_са=2*10 ^–3 м.; r_c=0,2 м.

Сила трения F_т: 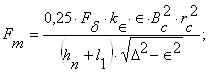 F_т=7,34*10 ^–3 H.

Сила сопротивления пружины в обобщенной форме:

- жесткость пружины.

 - начальная глубина внедрения якоря в обмотку.

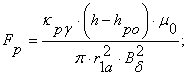 F_p=0,535 H.

Найдем демпфирующую силу:

- диаметр сердечника;

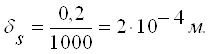- зазор между сердечником и магнитопроводом.

Коэффициент демпфирования вычислим по формуле:

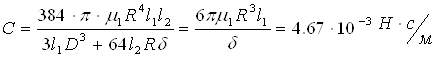
где v = 0,9 м/с. – усредненное значение скорости за время движения якоря.

 F_d=0.004 H,

где F_d – демпфирующая сила, зависящая от скорости движения якоря.

Рассчитаем коэффициенты выведения в пункте 1.3:

 p₁=2,411*10⁵, p₂=10,592

Подставляя эти коэффициенты в систему уравнений (1.3.3) можно рассчитать любые динамические параметры ЛЭМД.