Навигация
По контактным напряжениям
1. По контактным напряжениям.
При выпуске и уборке закрылков в воздухе в механизме данной схемы работают разные стороны профилей зубьев, поэтому при tp =t°=0.5 мин , a=1 и Nц.н=800 находим:
для ведущих зубьев
![]() циклов;
циклов;
для ведомых зубьев
![]() циклов.
циклов.
2. По изгибным напряжениям.
|
при r=0 и 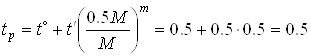 мин.
мин.
![]() циклов;
циклов;
![]() циклов;
циклов;
при r=-0.5 (реверс момента) соответственно числу реверсов
![]() циклов.
циклов.
§5. Определение допускаемых контактных напряжений для зубьев [I]
Их величины являются функцией твердости и числа циклов напряжения и ограничиваются верхним и нижним пределами :
![]() кГ/мм2;
кГ/мм2; ![]() кГ/мм2.
кГ/мм2.
Из следующей записи условия:
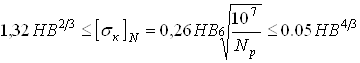 ,
,
где Np (по §4, п.1) после числовых подстановок:
для шестерни
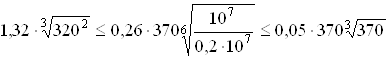 ,
,
получаем 68<125<132.
Значит,
![]() кГ/мм2 = 1294 Н/мм2;
кГ/мм2 = 1294 Н/мм2;
для колеса
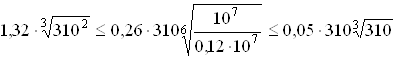 ,
,
получаем 68<137>133.
Значит,![]() кГ/мм2 =1343 Н/мм2.
кГ/мм2 =1343 Н/мм2.
Для расчета принимаем меньшее в паре
![]() кГ/мм2 = 1303 Н/мм2.
кГ/мм2 = 1303 Н/мм2.
§6. Предварительный подбор степени точности зацепления
В зубчатых передачах авиационных приборов наиболее распространены 5-я, 6-я, 7-я и 8-я степени точности зацепления в зависимости от окружной скорости и погонной нагрузки на зуб, а значит, и от твердости.
При НВmin в паре =310 можно принимать 7-ю степень точности [I], но, учитывая значительную ожидаемую скорость (n1=10 000 об/мин), задаемся
6-й повышенной степенью точности.
§7. Выбор относительной ширины зубчатых венцов
В узлах авиационных агрегатов обычно применяются зубчатые пары узкого типа как менее чувствительные к приборам валов и сниженной жесткости облегченных корпусов. При малой мощности (1÷5 квт) обычно ψL≤0,2[I]. Предварительно принимаем ψL=0,16.
§8. Выбор формы зуба в плане
Ввиду значительной ожидаемой скорости задаемся косым зубом с углом скоса по условию [I]
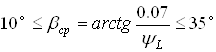 .
.
При ψL=0,16 имеем
![]() .
.
Принимаем ![]() ;
; ![]() .
.
§9. Определение поправочных коэффициентов, влияющих на расчетную величину погонной нагрузки
1. Неравномерность распределения погонной нагрузки по длине зубьев учитывается коэффициентом концентрации ![]() [I]
[I]
![]() ,
,
где К=1,2 – для косозубых колес;
![]() =0,45 – для несимметрично расположенного колеса по отношению к
=0,45 – для несимметрично расположенного колеса по отношению к
опорам и консольно сидящей шестерни;
Соб=1 – при ободе с тонким диском.
Подставляя числовые значения, получаем
![]() .
.
2. Дополнительные динамические нагрузки на зубья в зависимости от окружной скорости, твердости и степени точности, возникающие как следствие погрешностей изготовления зубьев по основному шагу, учитывает скоростной коэффициент [I]
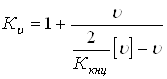 ,
,
где ![]() - окружная скорость, а
- окружная скорость, а ![]() - ее допускаемое значение в данном случае.
- ее допускаемое значение в данном случае.
Поскольку величина ![]() зависит от размеров передачи, которые еще не определены, задаемся в первом приближении
зависит от размеров передачи, которые еще не определены, задаемся в первом приближении
![]() .
.
3.Взаимоподдерживающее действие пар зубьев, находящихся в зацеплении, учитывает коэффициент профильного перекрытия К.
Для косых зубьев при расчете их по контактным напряжениям для 6-й степени точности предварительно принимаем [I]
![]() .
.
§10. Определение конусного расстояния из расчета на контактную прочность зубьев на номинальном режиме (первое приближение) [I]
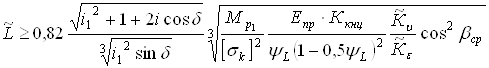 мм,
мм,
где δ=90°
![]() кГ/мм =
кГ/мм =![]() Н/мм;
Н/мм;
![]() =М1·Кд=427·1,05=448 кГмм =
=М1·Кд=427·1,05=448 кГмм =![]() Нмм.
Нмм.
Подставляя принятые и найденные входящие сюда величины, получаем
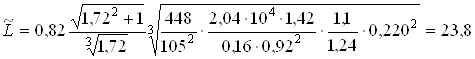 мм.
мм.
§11. Проверка выбора степени точности зацепления
0 комментариев