Навигация
Проектирование неравносмещенной эвольвентной зубчатой передачи и анализ зубчатого механизма
2 Проектирование неравносмещенной эвольвентной зубчатой передачи и анализ зубчатого механизма.
2.1 Проектирование зубчатой передачи
Исходные данные:
z1 = 15 ; z2 = 26 ; m = 10 .
Требуется:
- рассчитать геометрические параметры неравносмещенной эвольвентной зубчатой передачи внешнего зацепления из условия отсутствия подрезания;
- построить картину зацепления с изображением на ней теоретической и практической линий зацепления, рабочих участков профилей зубьев, дуг зацепления и сопряженных точек;
- рассчитать и построить графики удельных скольжений зубьев;
- дать письменный анализ диаграммы скольжения зубьев и определить коэффициент перекрытия передачи.
Для устранения подрезания ножки зуба малого колеса необходимо сделать смещение инструмента в положительную сторону на определенную величину, которое характеризуется коэффициентом смещения.
Подсчитываем передаточное число
U12 = z2/z1 = 1.73 .
По таблицам В.Н. Кудрявцева согласно чисел зубьев колес находим коэффициент относительного смещения х1 = 0.848 и х2 = 0.440.
Определяем инволюту угла зацепления
invaw = (2×(x1+x2)×tga/z1+z2) + inva ,
где a = 20о – стандартный угол зацепления.
По значению invawиз таблиц эвольвентной функции определяем угол зацепления проектируемой передачи aw= 26.5о.
Определяем межцентровое расстояние передачи
Аw = m(z1+z2)cosa/2×cosaw = 215.25 мм .
Определяем радиусы :
начальных окружностей
rw1 = Aw/U12+1 = 78.25 мм,
rw2 = Aw·U12/U12+1 = 136.4 мм;
делительных окружностей
r1 = mz1/2 = 75 мм, r2 = mz2/2 = 130 мм ;
основных окружностей
rb1 = r1×cosa = 70.5 мм ,
rb2 = r2×cosa = 122.16 мм ;
окружностей вершин зубьев
ra1 = r1+m (x1+ ha - Dy) = 91.58 мм ,
ra2 = r2+m (x2+ ha - Dy) = 142.5 мм ;
где ha= 1 коэффициент высоты головки зуба ;
Dy = 0.19 – коэффициент уравнительного смещения;
окружностей впадин зубьев
rf1 = r1 + m (x1 - hf- С ) = 70.98 мм ,
rf2 = r2 + m (x2 - hf- С ) = 121.9 мм ;
где hf = 1 – коэффициент высоты ножки зуба ,
С = 0.25 – коэффициент радиального зазора.
Качественные показатели зацепления
Шаг по делительной окружности
pt = p×m = 31.4 мм.
Толщина зубьев по делительным окружностям
s1 = 0.5pt + 2x1×m×tga = 21.87 мм , s2 = 0.5pt + 2x2×m×tga = 18.9 мм.
Ширина впадин из условия беззазорного зацепления
e1 = pt – s1 = 9.53 мм , e2 = pt – s2 = 12.5 мм.
![]()
![]() Коэффициент перекрытия
Коэффициент перекрытия
e = Öra12 – rb12 + Öra22 – rb22 - aw×sinaw/p×m×cosa = 1.23
Проверяем зуб малого колеса на отсутствие заострения
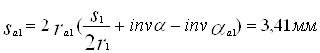
где aа1 = arccos ![]() .
.
Должно выполнятся условие Sa1 ³ 0.3m.
3.41 > 3 – условие выполняется.
Для построения картины зацепления выбираем масштаб
![]()
Проводим линию центров и в выбранном масштабе откладываем межосевое расстояние ![]() Из точек
Из точек ![]() и
и ![]() проводим дуги начальных окружностей, которые должны касаться друг друга в полюсе зацепления – Р. Через полюс зацепления проводим общую касательную Т-Т. К ней под углом
проводим дуги начальных окружностей, которые должны касаться друг друга в полюсе зацепления – Р. Через полюс зацепления проводим общую касательную Т-Т. К ней под углом ![]() проводим линию N-N
проводим линию N-N
Проведя дуги основных окружностей, убеждаемся в правильности проведенных построений – прямая N-N является общей касательной к основным окружностям в точках L1L2. Отрезок L1L2 является теоретической линией зацепления.
Для построения бокового профиля зуба первого колеса делим отрезок L1Р на равные части и несколько таких отрезка откладываем влево от точки L1 получаем 1,2,3…8. Дугами из центра L1 проецируем эти точки на основную окружность. Из полученных точек 1/,2/,3/…8/ проводим перпендикуляры к отрезкам ![]() и т.д. На этих перпендикулярах откладываем количество отрезков, соответствующих номеру перпендикуляра.
и т.д. На этих перпендикулярах откладываем количество отрезков, соответствующих номеру перпендикуляра.
Проводим дуги остальных окружностей – делительных, вершин зубьев и ножек зубьев.
От точки пересечения бокового профиля с делительной окружностью по последней влево откладываем толщину зуба, вправо – ширину впадины.
Определяем практическую линию зацепления - ![]() , которая является частью теоретической линии зацепления, отсекаемой окружностями вершин зубьев.
, которая является частью теоретической линии зацепления, отсекаемой окружностями вершин зубьев.
Рабочий участок профиля зуба первого колеса определится расстоянием по окружности вершины зуба до проекции точки ![]() по дуге с радиусом
по дуге с радиусом ![]() на боковой профиль. Аналогично определяем рабочий участок профиля зуба второго колеса.
на боковой профиль. Аналогично определяем рабочий участок профиля зуба второго колеса.
Для определения дуги зацепления изображаем пунктирной линией боковой профиль зуба на входе в зацепление (точка ![]() ) и на выходе (
) и на выходе (![]() ). Часть начальной окружности, заключенная между этими положениями бокового профиля будет являться дугой зацепления (ав). Для второго колеса построение аналогичное.
). Часть начальной окружности, заключенная между этими положениями бокового профиля будет являться дугой зацепления (ав). Для второго колеса построение аналогичное.
Используя дугу зацепления, определяем графически коэффициент перекрытия

Для построения сопряженной точки М2, выбранную на боковом профиле зуба точку М1, по дуге радиусом О1М1 проецируем на практическую линию зацепления (точка m). Радиусом О2m определяем положение точки М2 на боковом профиле зуба колеса 2.
Вычисляем коэффициенты удельных скольжений зубьев по формулам
![]() ,
, ![]()
![]() ,
,
где 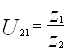 ,
,  - передаточные числа (без учета знака);
- передаточные числа (без учета знака);
L = L1L2 – длина теоретической линии зацепления
X – текущая координата, мм.
Расчетные данные сводим в таблицу 3
Таблица 3 – Значения коэффициентов удельного скольжения зубьев проектируемых колес
| Х | мм | 0 | 30 | 68 | 100 | 130 | 190 |
|
| - | -¥ | -2 | 0 | 0.48 | 0.73 | -¥ |
|
| - | 1 | 0.68 | 0 | -0.92 | -2.75 | 1 |
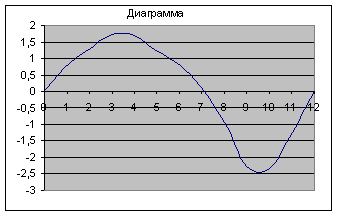
По полученным данным строим диаграмму скольжения, анализ которой показывает, что наибольшее скольжение наблюдается на ножке зуба второго колеса. Значительно скольжение на головке зуба первого колеса. Наименьшее скольжение имеет головка зуба второго колеса.
Похожие работы
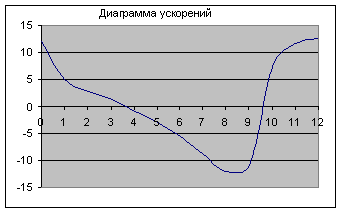
... 7,41 11,96 12,6 Графические 2,5 ; Диаграммы скоростей и ускорений: Рис.4 - Диаграмма скоростей Рис.5 - Диаграмма ускорений 2. Силовой анализ рычажного механизма Исходные данные: Масса кулисы m3=20 кг; Масса ползуна m5=52 кг; Сила полезного сопротивления Qпс=1550 Н. Схема механизма (Рис.6). ...
... , если к нему приложить уравновешивающую силу и моменты. 2.8 Сравним полученные значения Рур, рассчитанные по методу плана сил и методом рычага Жуковского. Вывод: Проведя силовой анализ механизма, определили реакцию опор, нашли уравновешивающую силу, выяснили, что на данный механизм влияют силы инерции. РАЗДЕЛ III Проектирование эвольвентного зубчатого зацепления Задачами ...
... 1.4 Построение диаграммы перемещений выходного звена. Диаграмма перемещений выходного звена получается в результате построения отрезков, которые берутся с чертежа плоского рычажного механизма в 12 положениях с учётом масштабного коэффициента 1.5 Построение диаграммы скоростей выходного звена. Диаграмма скоростей выходного звена получается в результате графического дифференцирования ...
... 24 0,00 0,00 14,10 14,10 9,30 9,30 58,02 58,02 2.4 Исследование механизма методом кинематических диаграмм Исследование механизмов методом диаграмм производится с целями: 1. Получения наглядного представления о законе движения интересующей нас точки или звена механизма. 2. Определения скоростей и ускорений точек или звеньев на основе известного закона перемещений точек или ...



0 комментариев