Анализ зубчатого механизма

2.2 Анализ зубчатого механизма

 

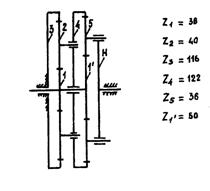
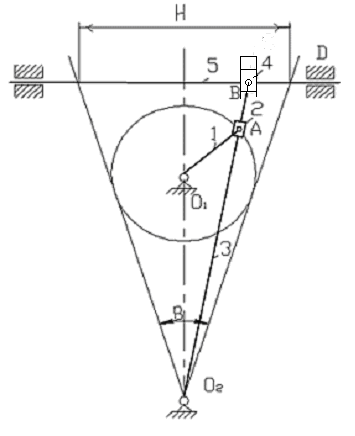
Для определения передаточного отношения графическим методом изображаем заданный механизм в масштабе, приняв произвольное значение модуля (m = 10). Обозначим на механизме все характерные точки – полюса зацеплений и центры колес. Проводим линию, перпендикулярную осям вращения колес и на нее проецируем все характерные точки. Так как ведущим звеном является колесо 1, то изображаем линейную скорость его конца (точка А) вектором Аа произвольной длины. Соединив точки а и О₁, получаем линию распределения линейных скоростей колеса 1. Соединяем точку В с точкой а, и на продолжении этой линии проецируем точку О₂, получим линию распределения линейных скоростей колеса 2. Соединив точки О₂, О₄ получим линию распределениялинейных скоростей колеса 4. На продолжении линии Аа проецируем точку А^/. Соединяем точку а^/ с точкой с получим линию распределения колеса 5. На эту линию проецируем точку О₅. Соединяем точку О₅ с точкой О_Н, получим линию распределения для конечного звена – водила.

Передаточное отношение определится через отрезки SH и S1

i_1Н = S₁/S_Н = 190/83 = 2.29

Так как отрезки SH и S1 находятся по одну сторону от SP, передаточное отношение получается со знаком плюс.

Имеем дифференциальный механизм

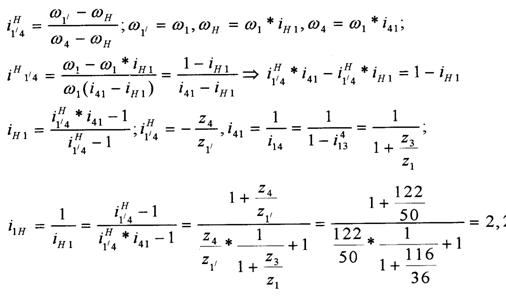
Di = 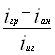×100% = 3.9 %

2.3 Проверка выполнения условий соосности, соседства и сборки планетарного механизма

 

Условие соосности представляет равенство межцентровых расстояний пар зубчатых колес

r₁ + r₂ = r₃ – r₂ или z₁ + z₂ = z₃ – z₂

36 + 40 = 116 – 40 76 = 76

Условие соосности выполняется.

Условие соседства определяет возможность размещения всех сателлитов по окружности их центров без задевания друг за друга.

sin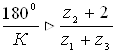

где К – число сателлитов

При К= 2 sin>0.28

Условие соседства выполняется.

Условие сборки определяет возможность одновременного зацепления всех сателлитов с центральным колесом. Это значит, что сумма чисел зубьев центральных колес будет кратной числу сателлитов.

где С – любое целое положительное число.

Условие сборки выполняется.

Таким образом, планетарная часть заданного зубчатого механизма удовлетворяет всем требованиям проектирования.

3 Силовой расчет рычажного механизма

Вариант 20

Исходные данные:

LOA= 0.2 LAB= 0.6 LBC= 0.5 LСD= 0.2 LDE= 0.7

LAS2= 0.2 LCS3= 0.1 LDS4= 0.3 XC=-0.22 YС=-0.45

m2= 60 m3= 50 m4= 50 m5=140 XЕ=-0.7

Pnc= -2Pj5 JS2= 0.1 JS3= 0.06 JS4= 0.12 w1= 60π,

где l_i – длины звеньев и расстояния до центров масс звеньев от их начальных шарниров, м;

J_si – моменты инерции звеньев, кгм²;

m_i – массы звеньев, кг;

w₁ – угловая скорость ведущего звена, с^-1;

P_nc - сила полезного сопротивления, приложенная к ползуну 5, Н;

P_j5 – сила инерции 5 звена, Н.

Требуется определить уравновешивающую силу методом выделения структурных групп и методом жесткого рычага Н.Е.Жуковского, давление во всех кинематических парах.

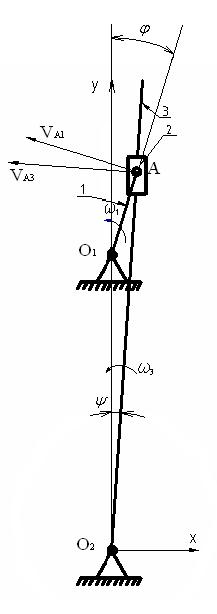
Вычерчиваем план механизма в масштабе m_l

m_l= l_OA/OA = 0.2/40 = 0.005 м/мм.

Строим план скоростей, повернутый на 90° в масштабе

m_v= V_A/Pa = w₁×l_OA/Pa = 60×3.14×0.2/94.2 = 0.4 ^м/_с/мм.

Скорость точки В определится в результате решения двух векторных уравнений

V_B = V_A+V_BA, V_B = V_C+V_BC.

Точку d на плане скоростей определяем по теореме подобия

BC/DC = Pb/Pd Pd = Pb×CD/BC = 64×40/100 = 25.6 мм. Для определения скорости точки Е составляем векторное уравнение V_Е = V_D+V_ED и решаем его. Строим план ускорений, повернутый на 180° в масштабе

m_a= a_A/pa=w₁²×l_OA/pa = (60×3.14)²×0.2/101.4 = 70 ^м/_с²/мм.

Ускорение точки В определяется относительно точек А и С

a_B = a_A+ aⁿ_BA+ a^t_BA, a_B = a_C + aⁿ_CB + a^t_CB,

aⁿ_BA = w₂²×l_AB = (ab×m_v / l_AB)²× l_AB = (84×0.4/0.6)²× 0.6 = 1881.6 ^м/_с²

aⁿ_BC = w₃²×l_BC = (Pb×m_v / l_BC)²× l_BC = (64×0.4/0.5)²× 0.5 = 1310.7 ^м/_с²

Длины отрезков, изображающих нормальные составляющие ускорений

aⁿ_BA и aⁿ_BC на плане ускорений, определяется с учетом масштаба m_a

an_BA= aⁿ_BA/m_a = 1881.6/70 = 26.9 мм

pn_BC= aⁿ_BC/m_a = 1310.7/70 = 18.7 мм

Положение точки d на плане ускорений определяем по теореме подобия

BC/DC = πb/πd πd = πb×CD/BC = 58×40/100 = 23.4 мм. Для определения ускорения точки Е составляем и решаем векторное уравнение a_Е = a_D+aⁿ_ED+a^t_ED. где aⁿ_ED=w₄²×l_ED=(V_ED/l_ED)²×l_ED= (de×m_v /l_DE)²×l_DE = (14×0.4)²/0.7 = 44.8 ^м/_с²/мм

Длина отрезка на плане ускорений

dn_ED= aⁿ_ED/m_a = 44.8/70 = 0.64 мм

Положение точек S₂, S₃, S₄ на плане ускорений определяем по теореме подобия из соотношений

АB/АS₂ = ab/aS₂ Þ aS₂ = ab×AS₂/AB = 45×40/120 = 15 мм

BC/CS₃ = pb/pS₃ Þ pS₃ = pb×CS₃/BC = 58×20/100 = 11.6 мм

DE/DS₄ = de/dS₄ Þ ds₄ = de×DS₄/DE = 19×60/140 = 8.14 мм

Определение сил инерции звеньев

При определении сил инерции и моментов учитываем, что план ускорений построен повернутым на 180°, поэтому знак минус в расчетах опускаем.

P_j2 = m₂×a_s2 = m₂×ps₂×m_a = 60×86×70 = 361200 H

M_j2 = J_s2×e₂ = J_s2×a^t_BA/l_AB = J_s2×n_BAb×m_a/l_AB = 0.1×39×70/0.6 = 455 H×м

P_j3 = m₃×a_s3 = m₃×ps₃×m_a = 50×12×70 = 42000 H

M_j3 = J_s3×e₃ = J_s3×a^t_BA/l_BС = J_s3×n_BСb×m_a/l_BС= 0.06×55×70/0.5 = 462 H×м

P_j4 = m₄×a_s4 = m₄×ps₄×m_a = 50×21×70 = 73500 H

M_j4= J_s4×e₄ = J_s4×a^t_ED/l_DE = J_s4×n_EDe×m_a/l_DE = 0.12×19×70/0.7 = 228 H×м

P_j5 = m₅×a_E = m₅×pe×m_a = 140×22×70 = 215600 H

Сила полезного сопротивления, приложенная к рабочему звену (5)

P_nc = -2 P_j5 = - 431200 H

Результирующая в точке Е R₅ = P_j5 + P_nc = -215600 H Наносим на план механизма вычисленные силы и моменты. В точки S₂, S₃, S₄ прикладываем силы инерции, а в точки А и Е, соответственно, уравновешивающую – Р_yи результирующую – R₅ силы.

Под действием приложенных сил механизм находится в равновесии. Выделяем первую структурную группу (звенья 4,5) и рассматриваем ее равновесие. В точках D и E для равновесия структурной группы прикладываем реакции R₃₄ и R₀₅ .

Составляем уравнение равновесия

SM_D = 0 , P_j4×h₄ µ_l + R₅×h₅ µ_l + R₀₅×h₀₅ µ_l - M_j4 = 0

R₀₅ = (-P_j4×h₄ µ_l - R₅×h₅ µ_l + M_j4)/h₀₅ µ_l = (-73500×2∙0.005- 215600×62∙0.005 + 228)/126∙ 0.005 = -106893.6 Н

SP_i = 0 . P_j4 + R₅ + R₀₅+R₃₄= 0 . Принимаем масштаб плана сил

m_p1 = P_j4/z_j4 = 73500/50=1470 H/мм

В этом масштабе строим силовой многоугольник, из которого находим

R₃₄ = z₃₄×m_p1 = 112×1470=164640 H

Выделяем и рассматриваем равновесие второй структурной группы (звенья 2,3). Для ее равновесия прикладываем:

в точке D – реакцию R₄₃ = - R₃₄ ;

в точке А – реакцию R₁₂ ;

в точке С – реакцию R₀₃ .

Составляем уравнения равновесия

SМ_В2 = 0 , P_j2×h₂ µ_l - R^t₁₂×AB×µ_l + M_j2 = 0 ,

R^t₁₂ = (P_j2×h₂µ_l+ M_j2 )/AB×µ_l = (361200×50∙0.005 + 455)/120×0.005 = 151258.3 H

SМ_В3 = 0 , P_j3×h₃×µ_l+ R^t₀₃×BC×µ_l +R₄₃×h₄₃ ×µ_l - M_j3 = 0

R^t₀₃ = - P_j3×h₃×µ_l-R₄₃×h₄₃ ×µ_l + M_j3/BC×µ_l,

R^t₀₃ = - 42000×76×0.005-164640×31×0.005 + 462/100×0.005 = - 82034.4 Н SP_i = 0, R^t₁₂ + P_j2 + R₄₃ + P_j3 + R^t₀₃ + Rⁿ₀₃ + Rⁿ₁₂ = 0 . Принимаем масштаб плана сил для данной структурной группы

m_p2 = P_j2/z_j2 = 361200/100 = 3612 H/мм

Из многоугольника сил определяем результирующую реакцию

R₁₂ = Rⁿ₁₂ + R^t₁₂ и ее величину

R₁₂ = z₁₂×m_p2 = 79×3612 = 285348 H

Рассматриваем равновесие оставшегося механизма первого класса. В точке О стойку заменяем реакцией R₀₁ произвольного направления.

Составляем уравнения равновесия

SМ₀ = 0 , P_y×OA - R₂₁×h₂₁ = 0 .

Уравновешивающая сила

P_y = R₂₁×h₂₁/OA = 79935.9 H

SP_i = 0 , P_y + R₂₁ + R₀₁ = 0 .

Масштаб плана сил

m_p3 = R₂₁/z₂₁ = 2850 H/мм

Из силового треугольника находим реакцию R₀₁

R₀₁ = z₀₁×m_p3 = 99×2850 = 282150 H

Определяем давление в кинематических парах.

Кинематическая пара В (звенья 2,3). Рассматриваем уравнение равновесия звена R₁₂ + P_j2 + R₃₂ = 0 .Для его решения используем план сил структурной группы (2,3). Замыкающий вектор z₃₂ показан пунктиром.

R₃₂ = z₃₂×m_p2 = 24×3612 = 86688 H Давление в кинематической паре Е (звенья 4,5) определится из решения векторного уравнения R₅ + R₀₅ + R₄₅ = 0 R₄₅ = z₄₅×m_p1 = 162×1470 = 238140 H Значения давлений во всех кинематических парах рассматриваемого механизма сводим в таблицу. Таблица 4 - Значения давлений в кинематических парах механизма

кинематические пары	0	А	В	С	Д	Е45	Е05
Обозначение	R01	R12	R32	R03	R34	R45	R05
Значение , Н	282150	285348	86688	122808	164640	238140	106893.6

Для определения уравновешивающей силы по методу Н.Е.Жуковского вычерчиваем план скоростей, повернутый на 90° в уменьшенном масштабе. На данном чертеже этот план скоростей совпадает с планом скоростей механизма. Используя теорему подобия, определяем на плане скоростей положения точек S₂, S₃, S₄.

АS₂/АВ = аk₂/ab Þ as₂ = ab×AS₂/AB = 84×40/120 = 28 мм

CS₃/CВ = Ps₃/Pb Þ Ps₃ = Pb×CS₃/CB = 64×20/100 = 12.8 мм

DS₄/DE = dk₄/de Þ ds₄ = de×DS₄/DE = 14×60/140 = 6 мм

Считаем преобразованные моменты:

M_j2^/ = M_j2×ab/l_AB = 63700 H×мм

M_j3^/ = M_j3×Pb/l_BC = 59136 H×мм

M_j4^/ = M_j4×de/l_DE = 4560 H×мм

В соответствующие точки плана скоростей прикладываем все действующие на механизм силы, в том числе и уравновешивающую.

Составляем уравнение равновесия для жесткого рычага Жуковского и решаем его.

P_y×Pa + M_j2^/ - M_j3^/ - M_j4^/ - P_j2×h_j2 - P_j3×h_j3 + R₅×Pe - P_j4×h₄ = 0 ,

P_y= (P_j2×h_j2 + P_j3×h_j3 - R₅×Pe  + P_j4×h₄ - M_j2^/ + M_j3^/ + M_j4^/)/ Pa = 48163.8 H

Вычисляем относительную ошибку определения уравновешивающей силы двумя методами

DР_у = [(Р_у¹ - Р_у¹¹)/ Р_у¹]×100% = |49935.9 – 48163.8/49935.9|×100% = 3.5 %

Ошибка не превышает 5% .