Изучите электроизмерительные приборы, используемые в работе, и запишите их паспортные данные
Аналогично определите чувствительность вертикально отклоняющих пластин, подавая напряжение на клеммы У
Построить график зависимости lnR=f(1/T), откладывая значения 1/Т по горизонтальной оси, a In R - по вертикальной
Собрать схему по рис. 2. Включать схему в цепь только с разрешения преподавателя!
Соберите цепь по схеме, указанной на рис. 3
Включить в сеть измеритель магнитной индукции (тесламетр, рис. 4). При необходимости провести установку нуля тесламетра
Метод магнитной фокусировки
Газоразрядную трубку расположите так, чтобы электронный пучок был направлен параллельно виткам катушек, при этом светящийся пучок примет вид кольца;
Для каждого значения тока вычислить значения Н и В
Поменять полярность источника, увеличивая обратный ток, перевести образец снова в насыщенное состояние
По формуле (13) вычислить индуктивность L катушки, подставляя в неё значения R и <Z>
Построить график
зависимости логарифмического декремента затухания от сопротивления контура
Навигация
По формуле (13) вычислить индуктивность L катушки, подставляя в неё значения R и <Z>
Электричество и магнетизм
189451
знак
18
таблиц
0
изображений
3. По формуле (13) вычислить индуктивность L катушки, подставляя в неё значения R и <Z>.
4. Результаты измерений и вычислений занести в таблицу:
| № | R, Ом | U, В | I, A | Z, Ом | <Z>,Ом | L, Гн |
Измерение ёмкости конденсатора
1. Собрать цепь по схеме (рис. 2).
2. Установить реостат на максимум сопротивления, подать переменное напряжение порядка 15 В. Изменяя сопротивление реостата, измерить силу тока I и напряжение U для трёх различных положений движка реостата. По формуле ХC = U/I определить ёмкостное сопротивление три раза и найти среднее значение <Хс>. Затем по формуле C=1/ωXc вычислить ёмкость конденсатора.
3. Результаты измерений и вычислений занести в таблицу:
| № | U, B | I, A | Xc, Ом | <XC>, Ом | С, Ф |
Проверка закона Ома для цепи переменного тока
1. Приборы соединить по схеме (рис.3), подать переменное напряжение порядка 15 В.
2. Измерить три значения тока I и напряжения U при разных положениях движка реостата и вычислить для каждого случая сопротивление Zизм = U/I, найти среднее значение <Zизм>.
3. Вычислить по формуле (12) значение Zвыч , подставляя полученные ранее значения R , L и С.
4. Сравнить результаты и вычислить относительную погрешность
.
5. Результаты измерений и вычислений занести в таблицу:
| № | U, B | I, A | Zизм, Ом | <Zизм>, Ом | Zвыч, Ом | δ |
Контрольные вопросы
1. Что называется переменным током?
2. В чем заключается явление самоиндукции?
3. Что называется индуктивностью, от чего она зависит, единицы ее измерения.
4. Каков сдвиг фаз между током и напряжением, если в цепи есть только активное сопротивление; покажите это с помощью векторной диаграммы.
5. Каков сдвиг фаз между током и напряжением, если в цепи есть только индуктивность или емкость; покажите это с помощью векторной диаграммы.
6. Как объяснить зависимость индуктивного и емкостного сопротивления от частоты переменного тока?
7. Как объяснить прохождение тока через конденсатор?
8. Ввести понятия эффективного значения тока и напряжения.
9. Вывести формулу закона Ома с помощью векторной диаграммы.
Литература, рекомендуемая к лабораторной работе:
22. Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.
23. Калашников С.Г. Электричество. – М.: Наука, 1977.
24. Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.
25. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.
26. Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.
27. Иродов И.Е. Электромагнетизм. Основные законы. –М.- С.-П.: Физматлит Невский диалект, 2001
28. Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.
29. Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.
30. Физический пракимкум. Электричество. Под редакцией В.И. Ивероновой. – М.: Наука, 1968.
31. Кортнев А.В., Рублев Ю.В., Куценко А.Н.. Практикум по физике. – М.: Высшая школа, 1965.
32. Руководство к лабораторным занятиям по физике. Под редакцией Л.Л. Гольдина, - М.: Наука, 1983.
ЛАБОРАТОРНАЯ РАБОТА № 15
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Цель работы:
Получить и наблюдать с помощью осциллографа затухающие электромагнитные колебания, определить логарифмический декремент затухания и его зависимость от параметров колебательного контура.
Идея эксперимента
Для возбуждения колебаний в контуре используется метод электрического удара: в цепь колебательного контура на конденсатор подаётся короткий электрический импульс, он заряжает конденсатор, и в цепи возникают затухающие колебания. В качестве источника электрических импульсов используется пилообразное напряжение генератора развёртки осциллографа. Для получения на экране осциллографа кривой U(t), можно воспользоваться схемой на рис. 1. На пластины осциллографа подается сигнал U пропорциональный току в контуре. Реле К 1-2 попеременно подключает конденсатор то к источнику импульсов, то к колебательному контуру, поэтому на экране осциллографа видна устойчивая картина (рис. 2). При этом условие синхронизации двух процессов - развёртки и затухающего колебания - выполняется автоматически, так как частота следования импульсов связана с частотой развёртки.
Теоретическая часть
Реальный колебательный контур
Замкнутая цепь, состоящая из катушки индуктивности и ёмкости, образует колебательный контур. Реальный колебательный контур обладает сопротивлением. Колебания в контуре можно вызвать, сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток, например, путём выключения внешнего магнитного поля, пронизывающего витки катушки.
Рассмотрим цепь, изображённую на рис.1. Если зарядить конденсатор от источника тока ε (ключ К в положении I), а затем замкнуть конденсатор на
|
|
электрического поля будет убывать, но зато возникает всё возрастающая энергия магнитного поля, обусловленного током, текущим через индуктивность. В катушке возникает э.д.с. самоиндукции, направленная так, чтобы поддержать ток. Поэтому в момент, когда напряжение на конденсаторе обратится в нуль, ток достигнет наибольшего значения.
Далее ток течёт за счёт э.д.с. самоиндукции и перезаряжает конденсатор, но уже до меньшего напряжения, так как часть энергии выделяется в виде джоулева тепла на сопротивлении R Затем те же процессы протекают в обратном направлении, после чего система приходит в исходное состояние.
Таким образом, в колебательном контуре периодически изменяются (колеблются) заряд на обкладках конденсатора, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергии электрического и магнитного полей.
На основании закона Ома
. 
, (1)
где U - напряжение на конденсаторе, εi - э.д.с. самоиндукции.
; 
, (2)
так как q=UC. Знак "минус" указывает, что положительным считается то направление тока, которое соответствует убыли заряда на конденсаторе. Из формул (2) находим:
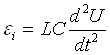. (3)
Из соотношений (I), (2) и (3) получается дифференциальное уравнение затухающих колебаний:
. (4)
Введём обозначения: ω0 = (1/LC)1/2 - циклическая частота собственных колебаний контура без затухания, β= R/2L коэффициент затухания. Тогда уравнение (4) можно записать в виде:
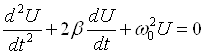. (5)
Решением этого уравнения будет выражение:
(б)
где 
(7)
циклическая частота свободных колебаний контура. Из уравнения (6) следует, что напряжение на конденсаторе со временем изменяется по гармоническому закону. Амплитуда колебаний 
убывает со временем по экспоненциальному закону. Вид затухающих колебаний представлен на рис. 2. Период колебаний выражается формулой:
. (8)
Если R достаточно мало по сравнению с L , то членом R2/4L2 можно пренебречь, и (8) переходит в формулу Томсона:
. (9)
Для характеристики затухания колебаний служит логарифмический декремент затухания – натуральный логарифм отношения двух амплитуд, отстоящих друг от друга по времени на один период.
,
(10)
 |
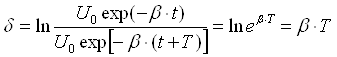. (11)
При сопротивлении 
, когда выражение (8) обращается в бесконечность, колебания в контуре не возникают, а процесс будет называться апериодическим.
Экспериментальная установка
Схема экспериментальной установки изображена на рис. 3. Емкость С,
индуктивность L и сопротивление R образуют колебательный контур. Колебания в контуре наблюдаются с помощью осциллографа. Для возбуждения колебаний служит генератор импульсов, присоединенный к контуру через конденсатор C1.
Конденсатор контура получает некоторый начальный заряд. В промежутках между импульсами в контуре совершаются свободные колебания, описываемые уравнением (5). Затухание колебаний определяется потерями энергии в катушке индуктивности L и сопротивлении R
Проведение эксперимента.
Изучение зависимости логарифмического декремента затухания от ёмкости
1. Собрать цепь по схеме (рис. 3), включив конденсатор электроёмкостью С= 13600 пФ.
2. Установить на магазине индуктивностей L = 100мГн и на магазине сопротивлений R = 200 Ом.
3. После проверки цепи включить осциллограф в сеть, добиться, чтобы на экране осциллографа было устойчивое изображение одного цуга затухающих колебаний.
4. Измерить несколько амплитуд затухающих колебаний, отстоящих на один период друг от друга.
5. Найти отношения A1/A2, А2/А3, А3/А4, вычислить среднее значение этих отношений и найти среднее значение логарифмического декремента затухания для данного контура по формуле (10).
6. Выразить логарифмический декремент затухания (11) через параметры R , L , С и вычислить его. Сравнить полученный результат с экспериментальным.
7. Заменить в схеме конденсатор на С = 6800 пФ и повторить все измерения и вычисления.
8. Сравнить значения δ при разных С и сделать вывод.
Изучение зависимости логарифмического декремента затухания от индуктивности
1.Включить конденсатор С = 13600 пФ, магазин индуктивностей на 100 мГн, магазин сопротивлений на 200 Ом.
2.Произвести все измерения и вычисления, обозначенные в пунктах 3-6 предыдущего задания.
3.Включить магазин индуктивностей на 50 мГн, повторить все измерения и вычисления.
4.Сравнить логарифмические декременты при разных L, сделать вывод.
Изучение зависимости логарифмического декремента затухания от сопротивления контура
1. Включить конденсатор С= 13600 пФ, магазин индуктивности на 100 мГн.
2. Меняя сопротивление контура через каждые 100 Ом, получить затухающие колебания, измерить амплитуды колебаний, вычислить для каждого случая логарифмические коэффициенты затухания.
3. Результаты измерений и вычислений занести в таблицу 1:
4. Пользуясь магазином сопротивлений, найти критическое сопротивление, при котором наступает апериодический процесс. Сравнить найденное значение с рассчитанным по формуле 
.
Похожие работы
... , хотя ему уже придавали иной смысл, нежели тот, который вкладывал в него Кулон.Введение понятия потенциалав электростатику Открытие закона Кулона было очень важным шагом в развитии учения об электричестве и магнетизме. Это был первый физический закон, выражающий количественные соотношения между физическими величинами в учении об электричестве и магнетизме. С помощью этого закона можно было ...
... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...
... в магнитном поле компасной стрелки в нем появляются токи, которые создают свое магнитное поле. Взаимодействие двух магнитных полей и дает «магнетизм вращения». «Теперь, – записал в своей рабочей тетради Фарадей, – когда мы знаем о существовании этих токов, явления, открытые Араго, можно объяснить, не приписывая их тому, что в меди образуется полюс, противоположный приближающемуся». Диск и магнит ...
... термин «электрический ток», понятие о направлении электрического тока и за полтора века предсказал возникновение науки об общих закономерностях процесса управления, связи и организованных системах – кибернетики. Ньютон электричества Звездный час в жизни Ампера наступил в сентябре 1820 г., когда он впервые узнал об открытии датским физиком Г. Х. Эрстедом (1819) действия электрического тока на ...
0 комментариев