Навигация
Аналогично определите чувствительность вертикально отклоняющих пластин, подавая напряжение на клеммы У
6. Аналогично определите чувствительность вертикально отклоняющих пластин, подавая напряжение на клеммы У.
7. Найдите средние значения чувствительности пластин jx и jy при различных значениях напряжений Uxи Uy 30, 50, 60 В.
8. Результаты измерений и вычислений занесите в таблицу;
| № | Ux, В | x, мм | Jx, мм/В | Uy, В | y, мм | Jy, мм/В |
Задание 2.. Измерение амплитудных значений напряжений
Осциллограф можно использовать для непосредственного измерения амплитудных значений переменного напряжения U0, тогда как вольтметр показывает эффективные значения напряжения. Известно, что если исследуемое напряжение изменяется по гармоническому закону
U= U0sin ωt , то эффективное значение напряжения:
Uэфф= U0/√2 .(2)
Это соотношение может быть использовано для определения истинного значения амплитуды переменного напряжения. Целью данного упражнения является измерение амплитудного значения напряжения с помощью осциллографа и его сравнение с вычисленным по формуле (2).
1. Соберите цепь по схеме рис. 6
2. Регулятор напряжения на ЛАТРе поставьте в крайнее левое положение;
3. Включите ЛАТР в сеть и установите напряжение 60 В;
4. Определите по координатной сетке длину световой линии L = 2x в мм;
5. Зная чувствительность трубки по X, найдите амплитудные значения напряжения по формуле ![]() :
:
6. Вычислите с помощью соотношения (2) амплитудное значение напряжения U0 теор. и оцените, с какой абсолютной погрешностью ∆U измерены амплитудные значения напряжения.
7. Проделайте аналогичные измерения и вычисления для напряжений 30, 40, 50 В
8. Результаты измерений и вычислений занесите в таблицу;
| № | Uэфф, В | L, мм | U0, В. | U0 теор, В | ∆U, B |
Задание 3. Визуальное наблюдение сигналов
Проведите наблюдение сигналов от звукового генератора, для этого:
а) на вертикальный вход осциллографа подайте напряжение с выхода звукового генератора;
б) при фиксированном значении частоты генератора развёртки, изменяя частоту сигнала звукового генератора, добейтесь на экране осциллографа появления осциллограмм с кратностью в I, 2, 3 и .более периодов напряжения генератора;
в) зарисуйте вид осциллограммы, укажите на ней периоды сигнала и развёртки.
г) аналогично проведите наблюдения сигналов, подавая напряжения с выхода звукового генератора на горизонтальный вход осциллографа;
Задание 4. Определение частоты сигналов методом фигур Лиссажу
Осциллограф можно использовать для определения частоты неизвестного гармонического колебания. Если на входы Х и У осциллографа подать гармонические сигналы различной частоты, то, участвуя в двух взаимно перпендикулярных колебаниях, электронный луч будет описывать фигуры Лиссажу, вид которых зависит от соотношения амплитуд, частот, фаз
подводимых напряжений (рис. 7) . Фигуры Лиссажу будут неподвижными, если подводимые частоты относятся как целые числа, например, 1:1, 1:2, 1:3, 2:1, 2:3, 3:4, а сдвиг фаз между колебаниями остаётся постоянным. Отношение частот νx/νy можно узнать по числу точек пересечения горизонтальной и вертикальной линий с фигурой Лиссажу. Цель настоящего упражнения – получить на экране осциллографа несколько фигур Лиссажу для соотношения частот 1:1, 1:2, 2:3, 1:3 с разностью фаз 0, π/4, π/2. Для этого:
а) соедините вертикальный вход осциллографа с выходом одного звукового
генератора, а горизонтальный вход – с выходом второго звукового генератора;
.б) отключите ДИАПАЗОН ЧАСТОТ на осциллографе;
в) включите в сеть осциллограф и звуковые генераторы, выведите и сфокусируйте полученную фигуру в центр координатной сетки;
г) на одном звуковом генераторе установите частоту 50 Гц;
д) подберите такие амплитуды колебаний, чтобы полученная фигура занимала среднюю часть экрана осциллографа;
е) вращением регулятора частоты второго звукового генератора добейтесь появления устойчивых фигур Лиссажу, зарисуйте фигуры на бумаге и определите по ним отношение частот νx/νy по числу точек пересечения фигуры с горизонталью nx и вертикалью ny .
Контрольные вопросы
1. Из каких блоков состоит электронный осциллограф? Каково назначение каждого блока?
2. От каких параметров зависит чувствительность ЭЛТ?
3. Как экспериментально определяется чувствительность осциллографа?
4. При каких условиях получают фигуры Лиссажу?
5. Какие условия должны выполняться, чтобы осциллограмма на экране ЭЛТ была неподвижна?
Литература, рекомендуемая к лабораторной работе:
1. Калашников С.Г. Электричество. – М.: Наука, 1977.
2. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.
3. Иродов И.Е. Электромагнетизм. Основные законы. –М.- С.-П.: Физматлит Невский диалект, 2001
4. Рублев Ю.В., Куценко А.Н., Кортнев А.В. Практикум по электричеству. – М.: Высшая школа, 1971.
5. Кортнев А.В., Рублев Ю.В., Куценко А.Н.. Практикум по физике. – М.: Высшая школа, 1965.
ЛАБОРАТОРНАЯ РАБОТА №3
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯЦель работы:
Ознакомиться с методом моделирования электростатических полей и экспериментально построить картину электростатического поля с помощью кривых равного потенциала и силовых линий.
Идея эксперимента
При конструировании электронных ламп, конденсаторов, электронных линз и других устройств часто требуется знать распределение электрического поля в пространстве, заключённом между электродами сложной формы. Наглядное представление о характере поля создаётся тогда, когда его напряжённость и потенциал известны во всём пространстве. Так как электроизмерительные приборы (электрометры, вольтметры) предназначены для измерения потенциалов, и, кроме того, расчёт скалярной величины произвести легче, чем векторной, то экспериментально обычно изучается распределение в пространстве потенциала. Система эквипотенциальных поверхностей полностью описывает конфигурацию электростатического поля, так как линии напряжённости всегда ортогональны к ним.
Обычно электростатическое поле исследуется путем перемещения в нем измерительных зондов, что легко может быть выполнено в жидких и газообразных диэлектрических средах. Однако электростатические измерения сопряжены с определенными трудностями, поскольку реальные диэлектрические среды обладают электропроводностью, зависящей от внешних условий (температуры, влажности и т.д.) Выход может быть найден в замене электростатического поля неподвижных зарядов полем постоянного электрического тока при условии, что потенциалы электродов (источников поля) поддерживаются постоянными, а электропроводность среды значительно меньше электропроводности электродов.
Теоретическая часть
Всякий неподвижный электрический заряд создает в окружающем пространстве электростатическое поле, которое обнаруживается при внесении пробных электрических зарядов в любую точку поля (подразумевается, что пробные заряды не искажают поля). Силовой характеристикой поля является его напряженность Е. Напряженность Е поля численно равна силе, с которой поле действует на единицу положительного заряда, помещенного в данную точку поля:
Е= F/q,
где q – величина пробного положительного заряда. Напряженность – векторная величина, совпадающая по направлению с силой.
Графически поле принято изображать с помощью силовых линий. Линия, касательная к которой в каждой точке совпадает по направлению с вектором напряженности электростатического поля, называется силовой линией. Следовательно, силовая линия определяет в каждой точке, через которую она проходит, направление силы, действующий на положительный заряд, помещенный в данную точку поля. Густота силовых линий характеризует численное значение напряженности. Через единичную площадку, перпендикулярную силовым линиям однородного поля, принято проводить число линий, равное Е.
Энергетической характеристикой поля является потенциал. Он измеряется работой, совершаемой силами поля при перемещении единичного положительного заряда из данной точки поля в бесконечность:
φ = A/q.
Потенциал электростатического поля является функцией координат. Можно выделить совокупность точек, для которых потенциал будет одним и тем же. Для поля, создаваемого точечным зарядом, такие совокупности точек будут образовывать концентрические сферические поверхности. Геометрическое место точек равного потенциала носит название эквипотенциальной поверхности. Любая линия на эквипотенциальной поверхности также эквипотенциальна.
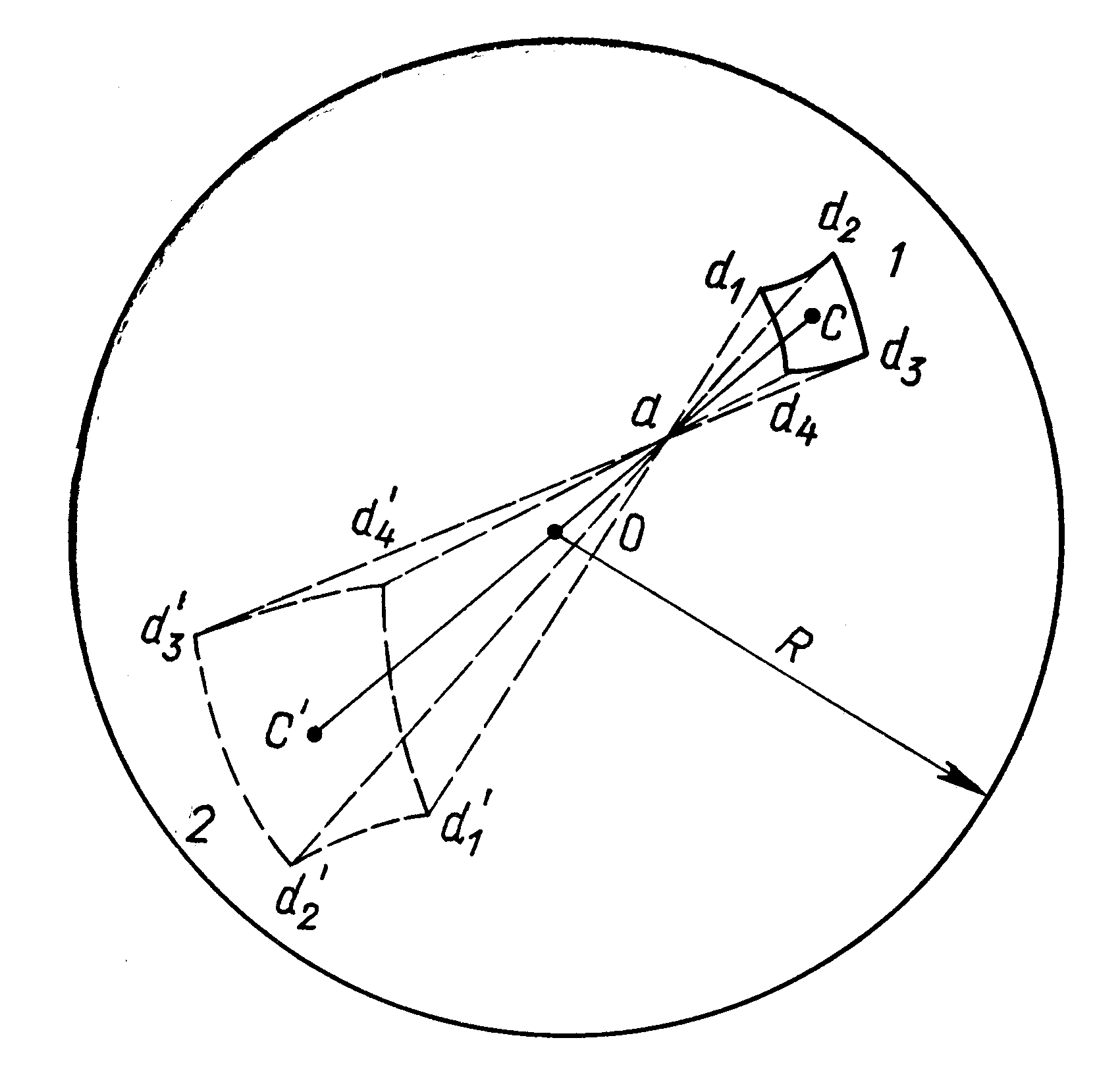
Рассмотрим две бесконечно близкие эквипотенциальные поверхности φ и φ+dφ (рис.1). Вектор напряженности E направлен по нормали n к эквипотенциальной поверхности φ и пересекает эквипотенциальные поверхности в точках a и b.
Расстояние ab является кратчайшим от точки b до второй эквипотенциальной поверхности. При перемещении единичного положительного заряда из точки а в b совершается работа dA, численно равнаяdA= Еdr.
Выражая ту же работу через разность потенциалов, получим:
dA=φ-(φ+d φ) = - dφ.Сравнивая полученные выражения, найдем
Е= - dφ/dr.
Величина dφ/dr характеризует быстроту изменения потенциала в направлении нормали n и называется градиентом потенциала. Градиент потенциала есть величина векторная и обычно обозначается grad
E= - grad φ.
Поля, для которых выполняется это соотношение, называются потенциальными или консервативными. Работа сил такого поля не зависит от формы пути перехода, а зависит от положения начальной и конечной точек.
Экспериментальная установка
Установка для изучения картины электростатического поля состоит из ванны, сделанной из материала с хорошими электроизолирующими свойствами, наполненной электролитом, проводимость которого мала, и двух электродов произвольной формы. Изучению подлежит электростатическое поле, создаваемое этими электродами. Для определения потенциала в любой точке поля используется метод зонда.
Для измерений используется схема (рис.2). представляющая собой мост, питаемый переменным током, в котором реохорд заменяется сопротивлениями межэлектродных промежутков. Здесь Э1 и Э2 - электроды, устанавливаемые в ванне, a Z - зонд. В качестве индикатора в данной схеме используется электронная лампа бЕ5С. Для питания моста служит переменный ток, так как при работе с постоянным током происходит так называемая поляризация, в результате которой падение потенциала происходит в основном вблизи электродов, ток через электролит уменьшается, и распределение потенциала между электродами искажается. Трансформатор Тр, питающий мост, помещён в одном корпусе с индикатором нуля (схема питания индикатора на рис. 2 не показана). На боковую панель корпуса выведены клеммы 3 В и 3 В, позволяющие снимать напряжение 12 В, и клеммы для включения индикатора в диагональ моста, обозначенные буквами С и Д. Напряжение подаётся в другую диагональ моста на делитель, представляющий собой два последовательно соединённых магазина сопротивлений R1 и R2 . Изменяя величины сопротивлений R1 и R2, можно получить различные значения потенциала ![]() средней точки делителя напряжения, соединённой с С. Если зонд Z находится в такой точке поля, потенциал которой равен потенциалу точки С делителя, то напряжение, подаваемое на управляющую сетку лампы-индикатора, будет равно нулю. В этот момент на светящемся экране индикаторной лампы тёмный сектор будет иметь наибольшую величину. Геометрическое место всех точек поля, для которых потенциал зонда будет равен заданному потенциалу при данных величинах R1 и R2, образует эквипотенциальную поверхность в исследуемом поле.
средней точки делителя напряжения, соединённой с С. Если зонд Z находится в такой точке поля, потенциал которой равен потенциалу точки С делителя, то напряжение, подаваемое на управляющую сетку лампы-индикатора, будет равно нулю. В этот момент на светящемся экране индикаторной лампы тёмный сектор будет иметь наибольшую величину. Геометрическое место всех точек поля, для которых потенциал зонда будет равен заданному потенциалу при данных величинах R1 и R2, образует эквипотенциальную поверхность в исследуемом поле.
Проведение эксперимента
1. Соберите цепь, схема которой приведена на рис. 2.
2. Приготовьте координатную сетку (желательно на миллиметровой бумаге). Нарисуйте на ней контуры и положение электродов.
3. На магазинах сопротивлений включите сопротивления порядка нескольких сотен омов.
4. Включите устройство в сеть переменного тока.
5. Найдите потенциал в некоторой точке электролитической ванны. Для этого опустите между электродами зонд Z и, подбирая с помощью магазинов сопротивления R1 и R2 , добейтесь, чтобы темный сектор в индикаторной лампе был максимальным. Потенциал вычислите по формуле: ![]() , где U - показание вольтметра. Перемещая зонд в поле между электродами, найдите не менее 10 точек с таким потенциалом. Найденные точки перенесите на заготовленную координатную сетку и соедините линией.
, где U - показание вольтметра. Перемещая зонд в поле между электродами, найдите не менее 10 точек с таким потенциалом. Найденные точки перенесите на заготовленную координатную сетку и соедините линией.
6. Изменяя R1 и R2, задайте новое значение потенциала ![]() , найдите соответствующие ему эквипотенциальные точки в межэлектродном промежутке и соедините их линией. Постройте не менее пяти эквипотенциальных линий с интервалом 1-2 В, около каждой линии напишите значение потенциала, которому она соответствует.
, найдите соответствующие ему эквипотенциальные точки в межэлектродном промежутке и соедините их линией. Постройте не менее пяти эквипотенциальных линий с интервалом 1-2 В, около каждой линии напишите значение потенциала, которому она соответствует.
7. Установите в ванне электроды другой формы и повторите все измерения для них.
8. Проведите пунктиром линии напряженности.
Контрольные вопросы
1. Дать понятие электростатического поля и его основных характеристик.
2. В чем заключается принцип суперпозиции полей?
3. Доказать, что эквипотенциальные поверхности всегда перпендикулярны силовым линиям.
4. В чем заключается метод электролитических моделей, его преимущество и недостатки.
5. Какие еще методы изучения электростатических полей вы знаете.
6. Почему в схеме, используемой в работе, пользуются переменным током, а не постоянным.
7. Нарисовать силовые линии и эквипотенциальные поверхности, создаваемые точечным зарядом и бесконечной проводящей плоскостью.
Литература, рекомендуемая к лабораторной работе:
Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.
6. Калашников С.Г. Электричество. – М.: Наука, 1977.
7. Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.
8. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.
9. Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.
10. Иродов И.Е. Электромагнетизм. Основные законы. –М.- С.-П.: Физматлит Невский диалект, 2001
11. Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.
12. Парсел Э. Курс физики Т.2 Электричество и магнетизм –М.: Наука, 1971.
13. Рублев Ю.В., Куценко А.Н., Кортнев А.В. Практикум по электричеству. – М.: Высшая школа, 1971.
14. Кортнев А.В., Рублев Ю.В., Куценко А.Н.. Практикум по физике. – М.: Высшая школа, 1965
.
ЛАБОРАТОРНАЯ РАБОТА №4
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОЙ ИНДУКЦИИ.Цель работы:
Экспериментальное изучение явления электростатической индукции.
Идея эксперимента:
Наиболее просто можно проверить законы электростатической индукции, экспериментируя с проводниками. Если две одинаковые тонкие металлические пластины, прижатые друг к другу плоскостями, внести в однородное поле E конденсатора (рис. 4) так, чтобы вектор нормали к пластинам совпал с вектором E, на боковых плоскостях составной пластины возникнут индуцированные заряды. При этом поверхностная плотность зарядов ![]() σ равна:
σ равна:
![]() , (1)
, (1)
где ε – диэлектрическая проницаемость среды между обкладками конденсатора, Еn – нормальная составляющая вектора напряженности электрического поля.
Если теперь развести тонкие пластины на небольшое расстояние так, чтобы они не соприкасались, и затем вынести из поля E, то на каждой пластине останется заряд
![]() (2)
(2)
где S – площадь пластины. Величину этого заряда можно измерить, если прикоснуться внесенными из поля пластинами к клеммам электростатического вольтметра и измерить напряжение U. Очевидно, что
![]() (3)
(3)
где ![]() и
и ![]() - емкость вольтметра и пластин соответственно.
- емкость вольтметра и пластин соответственно.
Проведя дополнительный опыт с известной емкостью СК, присоединенной ко входу вольтметра, измерим напряжение U2 равное:
![]() . (4)
. (4)
Зная U1 и U2, можно найти Q и СВ+СП.
Предложенный в работе метод определения величины найденного заряда может быть использован для измерения напряженности электростатического поля. Для измерения U1 и U2 в данной работе используется электростатический вольтметр (см. ниже)
Теоретическая часть
Проводники во внешнем электрическом поле
Проводниками называются материальные тела, в которых при наличии электрического поля возникает движение зарядов, т.е. электрический ток. Закон, связывающий силу тока протекающего по проводнику с разностью потенциалов, приложенной к его концам, был открыт экспериментально Г.С. Омом, дифференциальная форма которого имеет вид:
ј=γΕ,
где ј=I/S – плотность тока, а γ=1/ρ – удельная электрическая проводимость, зависящая от свойств материала, Е – напряженность электрического поля на концах проводника. По значению удельной электропроводности γ материалы делят на три класса: диэлектрики, полупроводники и проводники.
а) диэлектрики - вещества с малой электрической проводимостью. Идеальный диэлектрик характеризуется отсутствием проводимости, однако это может осуществиться лишь при 0 К. При температуре, отличной от 0 К, все материалы обладают определенной проводимостью и, следовательно, идеальных диэлектриков нет; диэлектриком принято называть материал, удельная электрическая проводимость которого γ < 10-5 См/м
б) полупроводники имеют удельную электрическую проводимость
10-5<γ<103 См/м;
в) для проводников γ > 103 См/м. В основном – это металлы. Наиболее хорошими проводниками среди них являются медь и серебро, у которых удельная электропроводность имеет порядок 107 См/м.
В электростатике рассматривается случай неподвижных зарядов, когда ј=0, следовательно, Е=0, т.е. внутри проводника при электростатическом равновесии электрическое поле отсутствует.
Из дифференциальной формы теоремы Остроградского- Гаусса
divE=ρ/ε0
следует, что при Е=0, ρ=0, т.е. внутри проводника отсутствуют объемные заряды. Это означает, что заряд проводника концентрируется на его поверхности в слое атомарной толщины. Конечно, внутри проводника имеются как положительные, так и отрицательные заряды, но они взаимно компенсируются и, в целом, внутренние области проводника нейтральны.
Если нейтральный проводник помещается во внешнее электрическое поле, то поверхностные заряды на проводнике перераспределяются так, что создаваемое ими внутри проводника поле полностью компенсирует внешнее поле, в результате чего суммарная напряженность поля внутри проводника равна нулю.
Явление перераспределения поверхностных зарядов на проводнике при его помещении во внешнее электрическое поле называется электрической индукцией. В случае электростатического внешнего поля индукция называется электростатической.
Под влиянием внешнего поля происходит также перераспределение поверхностных зарядов и в случае, если проводник заряжен.
Выделим на поверхности проводника элемент поверхности ΔS и построим прямой цилиндр высотой h, пересекающий поверхность. Применим к этому цилиндру теорему Гаусса:
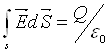 (5)
(5)
где S – поверхность цилиндра, Q – заряд в объеме цилиндра.
Внутри цилиндра заряд имеется только на поверхности проводника и характеризуется поверхностной плотностью ![]() σ и, следовательно, Q= σS. Внутри проводника поле равно нулю, поэтому поток Е через часть поверхности цилиндра, находящуюся в объеме проводника, равен нулю. Поток через часть поверхности цилиндра, находящуюся вне проводника слагается из потоков через основание цилиндра и его боковую поверхность. В пределе высоту h цилиндра возьмем сколь угодно малой (h→0), следовательно, и площадь боковой поверхности цилиндра и поток Е через боковую поверхность будут сколь угодно малыми. Поэтому в пределе h→0 останется лишь поток через основание цилиндра:
σ и, следовательно, Q= σS. Внутри проводника поле равно нулю, поэтому поток Е через часть поверхности цилиндра, находящуюся в объеме проводника, равен нулю. Поток через часть поверхности цилиндра, находящуюся вне проводника слагается из потоков через основание цилиндра и его боковую поверхность. В пределе высоту h цилиндра возьмем сколь угодно малой (h→0), следовательно, и площадь боковой поверхности цилиндра и поток Е через боковую поверхность будут сколь угодно малыми. Поэтому в пределе h→0 останется лишь поток через основание цилиндра:
![]() , (6)
, (6)
где Еn – нормальная компонента Е. Положительным направлением нормали в теореме Гаусса считается внешняя нормаль к замкнутой поверхности. В рассматриваемом случае это означает, что положительная нормаль направлена во внешнюю сторону от поверхности проводника. При h→0, с учетом (6) равенство (5) примет вид:
![]() ,
,
откуда
![]() .
.
Таким образом, нормальная компонента напряженности поля у поверхности проводника однозначно определяется поверхностной плотностью зарядов.
Найдем тангенциальную составляющую вектора напряженности Еτ. Рассмотрим замкнутый контур L, пересекающий поверхность проводника, верхняя часть которого идет параллельно поверхности вне проводника, а внутренняя часть – внутри проводника (рис 1). Внутри проводника напряженность Е=0, следовательно, отсутствует и тангенциальная компонента поля. Допустим, вне проводника Еτ≠0. Возьмем положительный заряд, и будем перемещать его по замкнутому контуру в направлении, указанном на рис. 1 стрелками. На участке АВ поле совершает положительную работу. Участки ВС и ДА могут быть сколь угодно малыми, следовательно, и работа может быть сколь угодно малой. При перемещении заряда на участке СД работа равна нулю, т.к. поле внутри проводника отсутствует. Таким образом, в результате перемещения заряда по замкнутому контуру электрическое поле производит положительную работу и больше в системе никаких изменений не происходит, что противоречит закону сохранения энергии. Следовательно, тангенциальная компонента напряженности поля должна быть равна нулю. Другими словами, равенство нулю тангенциальной компоненты электрического поля у поверхности проводника является следствием потенциальности электростатического поля и отсутствия поля внутри проводника.
Равенство Еτ= 0 означает, что напряженность электрического поля вблизи поверхности проводника направлено перпендикулярно поверхности и равно σ/ε0.
Из равенства нулю поля внутри проводника следует, что во всех точках проводника потенциал имеет одно и то же значение, т.е. любой проводник в электростатическом поле представляет собой эквипотенциальную область и его поверхность является эквипотенциальной.
Итак, в состоянии равновесия избыточных зарядов внутри проводника нет – вещество внутри проводника электрически нейтрально. Поэтому удаление вещества из некоторого объема внутри проводника (создание замкнутой полости) поля нигде не изменит, т.е. никак не отразится на равновесном расположении зарядов. Это значит, что избыточный заряд распределяется на проводнике с полостью также как и на сплошном – по его наружной поверхности.
Таким образом, если в полости нет электрических зарядов, электрическое поле в ней равно нулю. Внешние заряды, в частности, заряды на наружной поверхности проводника не создают в полости внутри проводника никакого электрического поля. Именно на этом основана электростатическая защита – экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Практически сплошной проводник-оболочка может быть заменен достаточно густой металлической сеткой.
Рассмотрим случай, когда полость не пустая, а в ней есть какой -то электрический заряд Q. Пусть внешнее пространство заполнено проводящей средой. Поле в ней при равновесии равно нулю, значит, среда электрически нейтральна. Так как поле внутри проводника равно нулю, то равен нулю и поток вектора Е сквозь замкнутую поверхность, окружающую полость. По теореме Гаусса это означает, что алгебраическая сумма зарядов внутри этой замкнутой поверхности также равна нулю. Таким образом, алгебраическая сумма индуцированных зарядов на поверхности полости равна по модулю и противоположна по знаку алгебраической сумме зарядов внутри этой полости.
При равновесии заряды, индуцированные на поверхности полости, располагаются так, чтобы полностью скомпенсировать снаружи полости поле зарядов, находящихся внутри полости.
Поскольку проводящая среда внутри электрически нейтральна, то она не оказывает никакого влияния на электрическое поле, поэтому если ее удалить, оставив только проводящую оболочку вокруг полости, от этого поле нигде не изменится и вне оболочки оно останется равным нулю. То есть, поле зарядов окруженных проводящей оболочкой и зарядов, индуцированных на поверхности полости равно нулю во всем внешнем пространстве.
Замкнутая проводящая оболочка разделяет все пространство на внутреннюю и внешнюю части, в электрическом отношении совершенно не зависящие друг от друга. Это надо понимать так: после любого перемещения зарядов внутри оболочки никаких изменений поля во внешнем пространстве не произойдет, а значит, распределение зарядов на внешней поверхности оболочки останется прежним. То же относится и к полю внутри полости (если там есть заряды) и к распределению индуцированных на стенках полости зарядов – они также останутся неизменными в результате перемещения зарядов вне оболочки. Это справедливо в рамках электростатики.
Электростатический вольтметр
Принцип действия вольтметра основан на электростатическом взаимодействии заряженных проводников. Измерительный механизм прибора состоит из неподвижного электрода 1 (рис 2), представляющего собой металлическую камеру, и подвижного алюминиевого электрода 2 в форме пластинки. Камера укреплена на изоляционной колонке 3 из вещества, обладающего большим сопротивлением на высоких частотах (керамики стеатита). Пластинка 2 закреплена на оси 4, которая установлена вертикально с помощью двух нитей 5 из бронзы (растяжки). Пружины 6, укрепленные на стойке 7, растягивают эти нити. Измеряемое напряжение подводится одним полюсом к камере, а другим – к пластинке. Камера и пластинка заряжаются
противоположными по знаку зарядами, и возникающая сила притяжения втягивает подвижную пластинку внутрь неподвижной камеры. Противодействующий момент создается упругими силами растяжек.
Для быстрого успокоения подвижной пластинки конец ее помещается в поле постоянного магнита 8. Торможение возникает благодаря силам, действующим со стороны магнитного поля магнита на ток, индуцируемый в той части пластинки, которая движется между полюсами магнита.
Так как обычно в таких электрических приборах моменты, действующие на подвижную часть малы, то для отсчета показаний прибора пользуются световым лучом, отраженным от небольшого легкого зеркала 9, укрепленного на оси 4.
Для уменьшения влияния внешних электрических полей прибор снабжен экраном, который заземляется. Теория электростатического вольтметра дает следующее выражение для угла отклонения α подвижной части:
![]() ,
,
где U- напряжение, подаваемое на вольтметр, С- емкость между электродами, k – коэффициент, зависящий от упругих свойств пружин. Из формулы видно, что угол α зависит как от квадрата напряжения U, так и от изменения емкости С. Подбором размеров и формы электродов удается сделать величину dC/dα постоянной. Поэтому, обычно шкала электростатических вольтметров имеет квадратичный характер.
Квадратичная зависимость угла отклонения от напряжения позволяет применять такие приборы для измерения не только напряжения постоянного, но и переменного тока до частоты порядка 30 МГц.
Эти приборы имеют малую входную емкость и высокое сопротивление изоляции; поэтому измерение постоянного напряжения происходит практически без потребления мощности самим прибором и с очень малым потреблением мощности при измерении переменного напряжения. Электростатические вольтметры пригодны для измерений высоких напряжений постоянного и переменного тока, причем при измерении высокого напряжения переменного тока не требуется применение специальных измерительных трансформаторов.
Внешний вид электростатического вольтметра приведен на рис 3. Шкала с горизонтальной прорезью для светового указателя расположена наклонно на передней панели прибора. Для установки светового указателя на нулевое положение имеется корректор, головка которого выведена на боковую сторону. На передней стенке прибора помещены штепсельная колодка для подключения питания осветителя и переключатель этого питания. Зажимы для включения вольтметра в схему расположены на задней панели.
Экспериментальная установка
Схема экспериментальной установки для измерения величины индуцированного заряда приведена на рис. 4
1 – источник питания с высоким входным сопротивлением; 2 – пластины конденсатора; 3 – измерительные пластины; 4 –изолирующие ручки; 5 – электростатический вольтметр; 6 – входные клеммы вольтметра.
Указания и рекомендации
1. Используемые в работе пластины укреплены на изолирующих ручках. Ручки должны быть чистыми, так как при загрязнениях изолирующие свойства ручек неконтролируемым образом ухудшаются, что искажает экспериментальные результаты.
2. Для удаления случайным образом образовавшегося заряда на пластинах и ручках, перед проведением эксперимента, их следует протереть заземленным проводящим материалом.
3. Присоединяемые к клеммам вольтметра пластины имеют собственную и взаимную емкость, зависящую от расположения пластин при прикосновении к клеммам вольтметра. Учитывайте это обстоятельство при проведении эксперимента.
4. Для уменьшения электростатических наводок следует поместить вольтметр в экранирующую металлическую коробку.
Проведение эксперимента:
1. Собрать схему по рис. 1.
2. Включить источник питания с высоким выходным напряжением.
3. Соединив измерительные пластины 3 вместе, внести их во внешнее электрическое поле, создаваемое между пластинами конденсатора 2.
4. Раздвинуть измерительные пластины и удалить их из поля конденсатора, не изменяя расстояние между ними.
5. Присоединить их к входным клеммам 6 электростатического вольтметра 5. Записать показания вольтметра U1.
6. Повторить пункты 3-5 с дополнительной известной емкостью Ск. Записать показания вольтметра U2.
7. Зная U1 и U2, из уравнений 3 и 4 определить СВ+СП и Q.
8. Повторить пункты 2-7 для 7-8 различных напряжений Определить площадь измерительных пластин
9. Вычислить поверхностные плотности зарядов σ и напряженности Е по формулам 1 и 2 для всех измеренных значений напряжений.
10. Построить график зависимость поверхностной плотности заряда σ, индуцированного на пластине, от напряженности поля в конденсаторе.
Контрольные вопросы
1. Проводники во внешнем электрическом поле.
2. Электростатическая индукция.
3. Электростатическая защита. Ее физический смысл.
4. Электростатический вольтметр. Принцип его действия.
5. Идея и методика проведения эксперимента.
6. Оценка погрешности эксперимента..
Литература, рекомендуемая к лабораторной работе:
4. Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.
5. Калашников С.Г. Электричество. – М.: Наука, 1977.
6. Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.
7. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.
8. Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.
9. Руководство к лабораторным занятиям по физике. Под редакцией Л.Л. Гольдина, - М.: Наука, 1983.
ЛАБОРАТОРНАЯ РАБОТА № 5
ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА ПО
ИЗУЧЕНИЮ ЕГО РАЗРЯДА
Цель работы:
Экспериментальное изучение процессов разрядки и зарядки конденсатора через сопротивления.
Идея эксперимента
При зарядке конденсатора через линейное сопротивление напряжение UC на его обкладках растет по закону:
![]()
т.е. с течением времени напряжение увеличивается, асимптотически приближаясь к эдс источника ε. В случае разряда конденсатора зависимость напряжения от времени имеет вид:
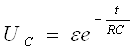 ,
,
т.е. с течением времени напряжение уменьшается по экспоненциальному закону, асимптотически приближаясь к нулю. Эти уравнения показывают, что процессы разрядки и зарядки происходят не мгновенно, а с конечной скоростью Быстрота установления электрического равновесия зависит от величины
τ=RC,
имеющей размерность времени и называемой временем релаксации. Величина τ показывает, через какое время после начала разрядки напряжение на конденсаторе уменьшается в e ≈ 2,72 раза. Ток же при разрядке и зарядке изменяется по закону:
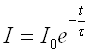 .
.
Если прологарифмировать это выражение, получим
Отсюда видно, что lnI является линейной функцией времени t с угловым коэффициентом 1/τ. (рис.1). Угловой коэффициент прямой есть скорость изменения функции по данному параметру и, следовательно, может
![]() .
.
быть рассчитан как тангенс угла наклона прямой lnI(t) к оси абсцисс. Т.е.
![]() .
.
Таким образом, время релаксации цепи τ можно определить, построив график зависимости lnI(t) по экспериментальным результатам. Величина сопротивления R рассчитывается из соотношения RI0=ε. После определения R и τ, можно найти C из соотношения:
С=τ/R. (1)
Теоретическая часть
В области электрических явлений большой интерес представляют переходные процессы, которые имеют место при разрядке и зарядке конденсаторов. Эти процессы используются во времязадающих узлах электронных схем, применяющихся в электронно-вычислительной технике (одно- и мультивибраторы), узлах развертки осциллографов, дисплеев, генераторов электрических колебаний звуковой и радиочастоты.
Задачи о зарядке и разрядке конденсатора, строго говоря, выходят за рамки учения о постоянных токах. Приводимые ниже решения получаются в предположении, что мгновенное значение тока одно и то же во всех поперечных сечениях провода, соединяющего обкладки конденсатора, а мгновенное электрическое поле такое же, как в электростатике при тех же зарядах на обкладках конденсатора. Токи и поля, удовлетворяющие этому условию, называются квазистационарными.
Если обкладки заряженного конденсатора (рис 2) соединить проводом, то по проводу потечет ток Пусть I, Q, и U - мгновенные значения тока, заряда на конденсаторе и напряжение на его обкладках Считая ток в проводе положительным, когда он течет от положительной обкладки к отрицательной, можно написать:
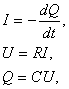
где С - емкость конденсатора, R - сопротивление провода. Исключая I и U, можно получить: 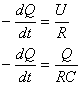
После интегрирования этого уравнения получается соотношение
![]() (1)
(1)
где Q0 - начальное значение заряда конденсатора (Q=Qo при t=0 ), а т - время релаксации. Дифференцируя (1) по времени t, можно найти закон изменения разрядного тока во времени:
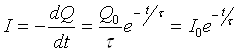
или
![]() , (2)
, (2)
где Iо = Q /τ - начальное значение тока, т.е. ток при t = 0.
Аналогично решается задача о зарядке конденсатора. Пусть в цепь конденсатора с емкостью С включен какой-нибудь источник тока с постоянной электродвижущей силой ε (рис.3).
Ток, идущий от источника, заряжает конденсатор. Электрические заряды, появляющиеся на обкладках конденсатора, препятствуют прохождению тока и уменьшают его. Можно записать, что
![]() ,
, ![]()
![]()
где R - полное сопротивление провода, соединяющего обкладки конденсатора и внутреннее сопротивление источника. Исключая снова I и U, получим уравнение ![]()
или ![]()
Это неоднородное уравнение сведется к однородному, если его записать в виде ![]() , так как εС = const. Решение этого уравнения получится в виде
, так как εС = const. Решение этого уравнения получится в виде ![]()
Значение постоянной интегрирования А найдется из условия, что в начальный момент времени конденсатор не заряжен, т. е. в этот момент времени Q = 0. Это дает А = -ε С, следовательно, ![]()
При t → ∞ заряд конденсатора стремится к предельному значению
Q =ε С. Для тока можно получить ![]() или
или ![]() (3)
(3)
где I0 = ε/R - максимальный ток в начальный момент времени. В дальнейшем он убывает по экспоненциальному закону.
Экспериментальная установка
Для экспериментального определения емкости конденсаторов в данной работе используется установка, принципиальная схема которой приведена на рис.4. Переключатель П служит для обеспечения разных режимов работы схемы. Положение 1-1 служит для измерения начального тока I0, положение 2-2 соответствует зарядке конденсатора, а 3-3 - его разрядке. С помощью переключателей П1 и П2 можно подключать различные сопротивления и конденсаторы
Проведение эксперимента
1. Экспериментальную установку подключить к самопишущему устройству.
2. Включить самопищущее устройство.
3. Включить источник питания ВУП-2, убедившись, что ручка регулировки напряжения источника на нуле.
4. Установить тумблеры переключателя рода работ в положение Io , R2, С2.
5. Вращая ручку регулировки напряжения установить ток в цепи 90 мкА, напряжение при этом 185 В.
6. Опустить перо на диаграммную ленту нажатием кнопки UP/DOWN на самопишущем устройстве и отметить ток 1о.
7. Привести диаграммную ленту в движение кнопкой START/STOP, одновременно поставив переключатель рода работ в положение ЗАРЯД.
8. Наблюдать за изменением силы тока, пока ток не станет равным нулю, подписать полученную диаграмму.
9. Остановить движение ленты нажатием кнопки START/STOP.
10.Вернуть ленту в начальное положение нажатием кнопки FEED
11.Выполнить пункты 3-10 для R 1C2, R2C1, R1 C1.
12.Срезать диаграммную ленту.
13.Построить логарифмические кривые ln I=f(t) для полученных диаграмм (см. рис.1)
14.По графикам определить τ - время релаксации.
15.Заполнить таблицу
16.Определить по формуле 1 C1 и С2.
Таблица 1.
| R 2C2 | R2 C1 | R1 C1 | R1 C2 | |||||
| I1 | ||||||||
| l2 | ||||||||
| ln I1 | ||||||||
| ln I2 | ||||||||
| τ | ||||||||
| R2 = C2= | R2= C1= | R1= C1 = | R1= С2= | |||||
Контрольные вопросы
1. Что такое электроемкость, от чего она зависит, ее единицы измерения?
2. Последовательное и параллельное соединение конденсаторов.
3. Вывести формулы электроемкости плоского, сферического и цилиндрического конденсатора.
4. Вывести законы изменения от времени тока при разрядке и зарядке конденсатора
5. Построить графики зависимости тока от времени.
6. Что такое время релаксации и от чего оно зависит?
7. Экспериментальная установка и правила пользования.
8. Как определить электроемкость из экспериментальных данных?
Литература, рекомендуемая к лабораторной работе:
15. Калашников С.Г. Электричество. – М.: Наука, 1977.
16. Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.
17. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.
18. Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.
19. Иродов И.Е. Электромагнетизм. Основные законы. –М.- С.-П.: Физматлит Невский диалект, 2001
20. Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.
21. Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.
ЛАБОРАТОРНАЯ РАБОТА № 6
ИЗУЧЕНИЕ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ
ПРОВОДНИКОВ И ПОЛУПРОВОДНИКОВ
Цель работы:
Изучить зависимость сопротивления от температуры у проводников и полупроводников, определить энергию активации и температурный коэффициент сопротивления.
Идея эксперимента:
В эксперименте производится измерение сопротивления проводников и полупроводников при различных температурах с помощью измерителя иммитанса Е 7-15, внешний вид которого приведен ниже на рис.2
Теоретическая часть
Проводимость проводников и полупроводников
Носителями электричества в металлах являются свободные электроны. Согласно классической теории электропроводности металлов свободные электроны ведут себя подобно молекулам идеального газа, совершают беспорядочное тепловое движение. При включении внешнего электрического поля на хаотическое тепловое движение электронов накладывается их упорядоченное движение в направлении, противоположном направлению поля. Между двумя последовательными соударениями с ионами кристаллической решётки электроны движутся под действием поля с ускорением и приобретают определённую энергию. Эта энергия передаётся полностью или частично положительным ионам при неупругих соударениях и превращается в тепло. Поэтому при прохождении тока металлы нагреваются. Таким образом, электрическое сопротивление металлов обусловлено неупругими соударениями свободных электронов с положительными ионами узлов кристаллической решётки металла.
С увеличением температуры проводника тепловое движение ионов становится более интенсивным, возрастает амплитуда колебаний их относительно положения равновесия, поэтому сопротивление проводника увеличивается. Температурная зависимость сопротивления характеризуется температурным коэффициентом сопротивления, который численно равен относительному изменению сопротивления проводника при изменении температуры на один градус:
![]() . (1)
. (1)
В общем случае α является функцией температуры и зависит от материала проводника. Для многих металлов при температуре от 0 до 100°С зависимость сопротивления от температуры в первом приближении может быть представлена в виде
![]() , (2)
, (2)
где R0 - сопротивление при 0° С, t - температура проводника в градусах Цельсия. Тогда температурный коэффициент сопротивления
![]() (3)
(3)
В классической теории металлов считалось само собой разумеющимся, что электроны проводимости могут обладать любыми значениями энергии. Согласно квантовой теории энергия электронов в любом кристаллическом теле (в частности, в металле) так же, как и энергия электронов в атоме, квантуется. Это означает, что она может принимать лишь дискретные значения, называемые уровнями энергии. Дозволенные уровни энергии в кристалле группируются в зоны.
Чтобы понять происхождение зон, рассмотрим воображаемый процесс объединения атомов в кристалл.
Пусть первоначально имеется N изолированных атомов какого- либо вещества. Каждый электрон любого атома обладает одним из разрешенных значений энергий, то есть занимает один из дозволенных энергетических уровней. В основном, невозбужденном состоянии атома суммарная энергия электронов имеет минимально возможное значение. Поэтому, казалось бы, все электроны должны находиться на самом низком уровне. Однако электроны подчиняются принципу запрета Паули, который гласит, что в любой квантовой системе на каждом энергетическом уровне может находиться не более двух электронов, причем собственные моменты(спины) электронов, занимающих одновременно один и тот же уровень, должны иметь противоположные направления. Следовательно, на самом низком уровне может разместиться только два электрона, остальные заполняют попарно более высокие уровни.
Пока атомы изолированы друг от друга, они имеют полностью совпадающие схемы энергетических уровней. Заполнение уровней электронами осуществляется в каждом атоме независимо от заполнения аналогичных уровней в других атомах. По мере сближения атомов, между ними возникает все усиливающееся взаимодействие, которое приводит к изменению положения уровней. Вместо одного одинакового для всех N атомов уровня возникают N очень близких, но не совпадающих уровней. Таким образом, каждый уровень изолированного атома расщепляется в кристалле на N густо расположенных уровней, образующих полосу или зону.
Величина расщепления для разных уровней не одинакова. Уровни, заполненные в атоме более близкими к ядру (внутренними) электронами, возмущаются меньше, чем уровни, заполненные внешними электронами. Заметно расщепляются лишь уровни, занимаемые валентными электронами. Такому же расщеплению подвергаются и более высокие уровни, не занятые электронами в основном состоянии атома.
При достаточно малых расстояниях между атомами может произойти перекрывание зон, соответствующих двум соседним уровням атома. Число уровней в такой сливающейся зоне равно сумме количеств уровней, на которые расщепляются оба уровня атома.
Взаимодействующие атомы представляют собой единую квантовую систему, в пределах которой действует принцип запрета Паули. Следовательно, 2N электронов, которые заполняли какой-то уровень в изолированных атомах, разместятся в кристалле попарно (с противоположными спинами) на N уровнях соответствующей полосы.
Нижние, образованные слабо расщепленными уровнями зоны заполняются электронами, каждый из которых не утрачивает в кристалле прочной связи со своим атомом.
Дозволенные значения энергии валентных электронов в кристалле объединяются в зоны, разделенные промежутками, в которых разрешенных значений энергий нет. Эти промежутки называются запрещенными зонами. Ширина разрешенных и запрещенных зон не зависит от размеров кристалла. Таким образом, чем больше атомов содержит кристалл, тем теснее располагаются уровни в зоне. Ширина разрешенных зон имеет величину порядка нескольких электрон-вольт. Следовательно, если кристалл содержит 1023 атомов, то расстояние между уровнями в зоне составляет ~ 10-23 эВ.
При абсолютном нуле энергия кристалла должна быть минимальной. Поэтому валентные электроны заполняют попарно нижние уровни разрешенной зоны, возникшей из того уровня, на котором находятся валентные электроны в основном состоянии атома (валентная зона). Более высокие разрешенные зоны будут от электронов свободны. В зависимости от степени заполнения валентной зоны электронами и ширины запретной зоны возможны три случая, изображенные на рисунке 1. В случае а) электроны заполняют валентную зону не полностью, поэтому достаточно сообщить электронам, находящимся на верхних уровнях, совсем небольшую энергию (~ 10 -23÷10-22 эВ) для того, чтобы перевести их на более высокие уровни. Энергия теплового движения составляет при 1К величину порядка 10-4эВ. Следовательно, при температурах отличных от 0 К часть электронов переводится на более высокие уровни. Дополнительная энергия, вызванная действием на электрон электрического поля, также оказывается достаточной для перевода на более высокие уровни. Поэтому электроны могут ускоряться электрическим полем и приобретать дополнительную скорость в направлении, противоположном направлению поля. Таким образом, кристалл с подобной схемой энергетических уровней будет представлять собой металл. Частичное заполнение валентной зоны (в случае металла ее также называют зоной проводимости) может произойти, если на последнем занятом уровне в атоме находится только один электрон; или имеет место перекрывание зон. В первом случае N электронов проводимости заполняют попарно только половину уровней валентной зоны. Во втором случае число уровней в зоне проводимости будет больше N, так, что даже если количество электронов проводимости равно 2N, они не смогут занять все уровни зоны.
В случаях б) и в) уровни валентной зоны полностью заняты электронами – зона заполнена. Для того чтобы увеличить энергию электрона, необходимо сообщить ему количество энергии, не меньшее, чем ширина запретной зоны ΔW. Электрическое поле сообщить электрону такую энергию не в состоянии. При этих условиях электрические свойства кристалла определяются шириной запретной зоны ΔW. Если ΔW невелико (порядка нескольких десятых эВ) энергия теплового движения оказывается достаточной для того, чтобы перевести часть электронов в верхнюю свободную зону. Эти электроны будут находиться в условиях, аналогичных тем, в которых находятся валентные электроны в металле. Свободная зона окажется зоной проводимости. Одновременно станет возможным переход электронов валентной зоны на ее освободившиеся верхние уровни. Такое вещество называется электронным полупроводником.
Если ширина запрещенной зоны ΔW велика (порядка нескольких эВ), тепловое движение не сможет забросить в свободную зону заметное число электронов. В этом случае кристалл оказывается изолятором.
Таким образом, квантовая теория объясняет с единой точки зрения существование хороших проводников (металлов), полупроводников и изоляторов.
Итак, полупроводниками являются кристаллические вещества, у которых валентная зона полностью заполнена электронами, а ширина запрещённой зоны невелика (не более 1 эВ). Полупроводники обязаны своим названием тому обстоятельству, что по величине электропроводности они занимают промежуточное положение между металлами и диэлектриками. Однако, характерным для них является не величина проводимости, а то, что их проводимость растёт с повышением температуры (у металлов она уменьшается).
Электрическое поле не может перебросить электроны из валентной зоны в зону проводимости. Поэтому полупроводники ведут себя при абсолютном нуле как диэлектрики. При температурах, отличных от 0 К, часть электронов из валентной зоны переходит в зону проводимости, в результате чего в полупроводнике возникают свободные носители зарядов. С повышением температуры число таких носителей растёт и, следовательно, увеличивается электропроводность полупроводника, а значит, уменьшается сопротивление. Зависимость сопротивления полупроводников от абсолютной температуры в определённых температурных интервалах описывается формулой
![]() , (4)
, (4)
где А - константа, k - постоянная Больцмана, ΔЕ - энергия активации. Под энергией активации понимается энергия, которую нужно затратить, чтобы перевести электрон из валентной зоны в зону проводимости. Логарифмирование уравнения (4) даёт
![]() . (5)
. (5)
График зависимости ln(R)=f(1/T) представляет собой прямую, угловой коэффициент которой равен ΔЕ/К. Построив график зависимости (5), этот угловой коэффициент можно определить по формуле
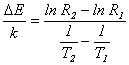 (6)
(6)
для любых двух точек, лежащих на прямой, а затем найти энергию активации ΔЕ.
Экспериментальная установка
Исследуемые проводник и полупроводник помещаются в термостат, заполненный непроводящей жидкостью. В нижней части термостата помещен нагреватель. Температура измеряется термометром. Сопротивления проводника и полупроводника измеряются одновременно с помощью измерителя иммитанса (рис.2). Для проведения измерения достаточно подключить проводник (полупроводник) к зажимам и установить нужный режим измерения. Нажатием кнопки «Параметр» установить прибор в режим измерения RG. Так как истинная температура проводника и полупроводника может несколько отличаться от показаний термометра в условиях нагревания и охлаждения, то сопротивление следует измерять дважды: при нагревании, а затем при охлаждении, и вычислять среднее значение.
Проведение эксперимента
1. Исследуемые проводник и полупроводник подключить к клеммам измерителей иммитанса в качестве неизвестного сопротивления;
2. Измерить их сопротивления при комнатной температуре;
3. Включить нагреватель и измерять сопротивления Rпов. через каждые 4-5° С при повышении температуры до 50-60° С;
4. Выключить нагреватель и произвести измерения сопротивлений Rпон. проводника и полупроводника при их охлаждении до комнатной температуры;
5. Результаты измерений занести в таблицы 1 и 2;
6. Определить среднее значение сопротивлений, измеренных при повышении и понижении температуры;
7. Построить график зависимости проводника R= f(T), откладывая по горизонтальной оси температуру, а по вертикальной – сопротивление;
8. Из графика определить R0 и α следующим образом: продлить полученную прямую до пересечения с осью R. Точка пересечения даст значение R0 . Значение коэффициента α вычислить по формуле (3), воспользовавшись данными графика.
Похожие работы
... , хотя ему уже придавали иной смысл, нежели тот, который вкладывал в него Кулон.Введение понятия потенциалав электростатику Открытие закона Кулона было очень важным шагом в развитии учения об электричестве и магнетизме. Это был первый физический закон, выражающий количественные соотношения между физическими величинами в учении об электричестве и магнетизме. С помощью этого закона можно было ...
... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...
... в магнитном поле компасной стрелки в нем появляются токи, которые создают свое магнитное поле. Взаимодействие двух магнитных полей и дает «магнетизм вращения». «Теперь, – записал в своей рабочей тетради Фарадей, – когда мы знаем о существовании этих токов, явления, открытые Араго, можно объяснить, не приписывая их тому, что в меди образуется полюс, противоположный приближающемуся». Диск и магнит ...
... термин «электрический ток», понятие о направлении электрического тока и за полтора века предсказал возникновение науки об общих закономерностях процесса управления, связи и организованных системах – кибернетики. Ньютон электричества Звездный час в жизни Ампера наступил в сентябре 1820 г., когда он впервые узнал об открытии датским физиком Г. Х. Эрстедом (1819) действия электрического тока на ...

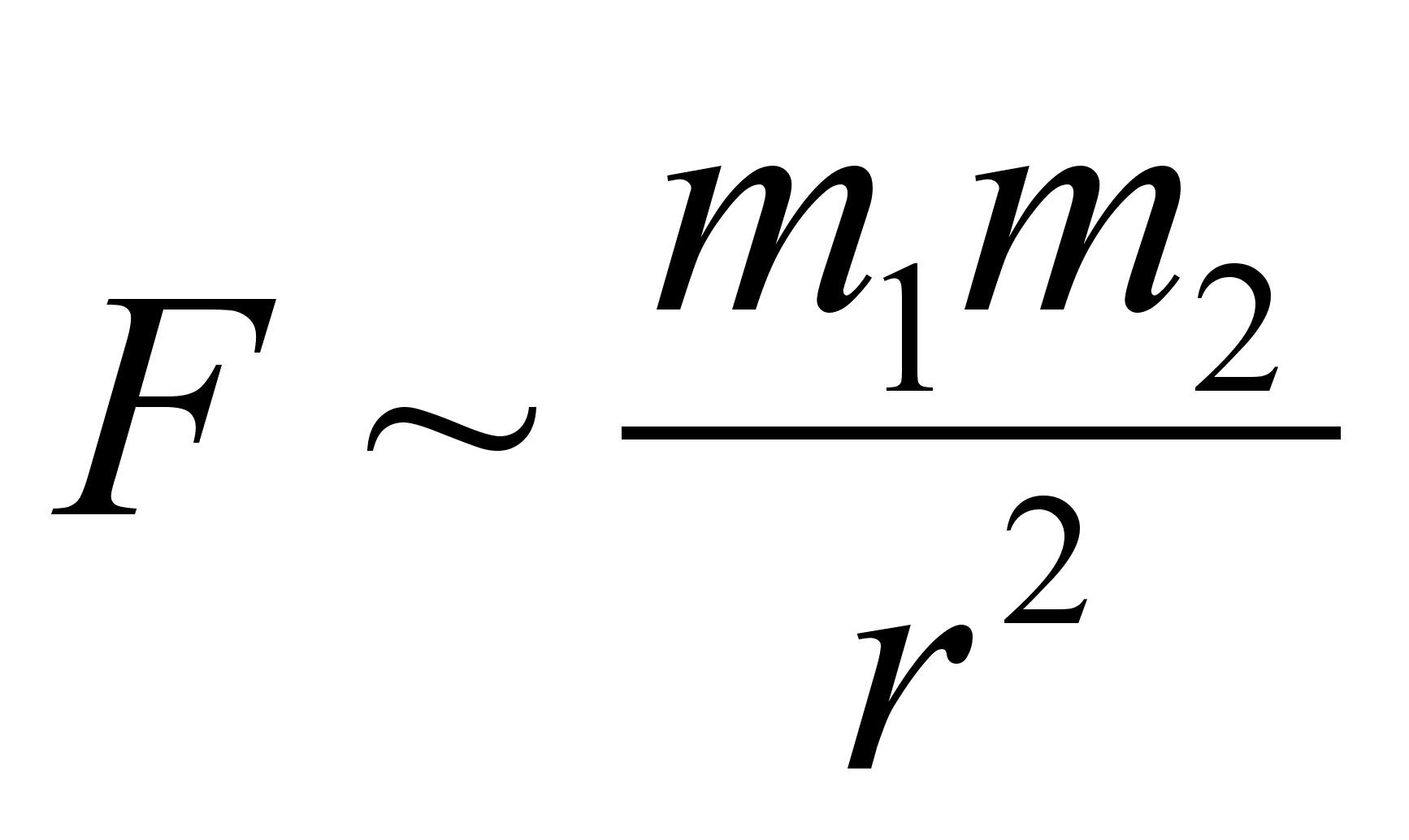


0 комментариев