Собрать схему по рис. 2. Включать схему в цепь только с разрешения преподавателя!

1.  Собрать схему по рис. 2. Включать схему в цепь только с разрешения преподавателя!

2.  Включить цепь накала и установить ток накала I_и=5,1 А. Меняя анодное напряжение от 0 до 20 В через 5 В, а затем от 20 до 100 В через каждые 10 В, снять анодную характеристику лампы.

3.  Снять анодные характеристики лампы при меньших токах накала – 5,0 А и 4,9 А. Занести все измерения в таблицу 1:

Таблица 1

Iи = 5, 1 А		Iи = 5, 0 А		Iи = 4, 9 А
Ua, В	Iа, мкА	Ua, В	Iа, мкА	Uа. В	Ia, мкА

4.  Построить графики зависимостей I_a=f (U_a) по данным измерений. Оп­ределить для всех кривых ток насыщения.

5.  Вычислить значения lgI_a и lgU_aдля одного из токов на­кала. Результаты занести в таблицу 2:

Таблица 2

№

Ia, мкА

lgJa

ua, В

lg ua

6.  Построить график зависимости lg I_a= f(lg U_a). При постро­ении графика брать один и тот же масштаб, как по оси ординат, так и по оси абсцисс.

7.  Выбрать линейный участок полученного графика, определить численное значение коэффициента С и вычислить угловой коэффици­ент n по формуле:

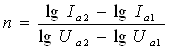
для двух любых точек линейного участка.

8.  Сравнить полученное значение углового коэффициента с пока­зателем степени в формуле (5).

 

Контрольные вопросы

 

1.  Электронная эмиссия, ее виды. Работа выхода

2.  Вольт-амперная характеристика вакуумного диода.

3.  Закон Богуславского-Ленгмюра.

4.  Каковы причины отклонения от закона Богуславского-Ленгмюра в реальных электронных лампах.

5.  Зависимость тока насыщения от температуры, формула Ричардсона-Дэшмена.

6.  Электронная лампа как выпрямитель.

7.  Как определить поток и плотность потока электронов из катода?

8.  Методика проведения эксперимента.

 

Литература, рекомендуемая к лабораторной работе:

 

1.  Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.

2.  Калашников С.Г. Электричество. – М.: Наука, 1977.

3.  Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.

4.  Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.

5.  Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.

6.  Иродов И.Е. Электромагнетизм. Основные законы. –М.- С.-П.: Физматлит Невский диалект, 2001

7.  Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.

8.  Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.

9.  Рублев Ю.В., Куценко А.Н., Кортнев А.В. Практикум по электричеству. – М.: Высшая школа, 1971.

ЛАБОРАТОРНАЯ РАБОТА № 8

ИЗУЧЕНИЕ ЭЛЕКТРОПРОВОДНОСТИ ЖИДКОСТИ.

 

Цель работы:

Экспериментальное изучение законов протекания тока через элек­тролит. Определение числа Фарадея, заряда электрона, коэффициента диффузии, подвижности и скорости ионов.

 

Идея эксперимента

 

Для визуализации движения ионов используется водный раствор перманганата калия (KMnO₄) малой концентрации. Измеряя перемещение фиолетовых ионов MnO₄ можно определить их скорость υ и подвижность b, зависимость этих величин от напряженности поля Е, в котором находятся ионы. В измеряемые величины вносит вклад диффузия ионов MnO₄ в растворе KNO₃. Проводя измерения с полем и без поля можно определить коэффициент диффузии D и учесть его вклад в величиныυ и b.

Измерив массу вещества, выделившегося на электроде, можно определить число Фарадея F и заряд электрона e.

 

Теоретическая часть.

 

Вещества, в которых при прохождении тока происходят химические превращения, называются проводниками второго рода или электролитами. К их числу принадлежат растворы солей, щелочей или кислот в воде и некоторых других жидкостях, а также расплавы солей, являющихся в твердом состоянии ионными кристаллами

Носителями тока в электролитах служат ионы, на которые диссоциируют (расщепляются) в растворе молекулы растворенного вещества. Образовавшиеся ионы начинают странствовать по раствору. Если ионы разных знаков сблизятся на достаточно малое расстояние, они могут объединиться снова в молекулу. Этот процесс, противоположный процессу диссоциации, называется рекомбинацией или молизацией ионов. В растворе идут одновременно оба процесса. Когда количество молекул, диссоциирующих в единицу времени, станет равным количеству молекул, возникающих за то же время вследствие рекомбинации, установится равновесное состояние. Этому состоянию соответствует определенная степень диссоциации, которую принято характеризовать коэффициентом диссоциации α, показывающим, какая часть молекул растворенного вещества находится в диссоциированном состоянии.

Пусть в каждой единице объема раствора имеется n молекул растворенного вещества, из которых α∙ n диссоциировано, а (1-α) n – не диссоциированы. Количество элементарных актов диссоциации в одну секунду в единице объема тем больше, чем больше имеется в наличии нерасщепленных молекул, т.е. равно:

η₁= А(1-α)n,

где А – коэффициент, зависящий от природы электролита и его температуры. Число актов рекомбинации пропорционально числу соударений разноименных ионов, которое пропорционально концентрации положительных и концентрации отрицательных ионов, т.е. равно:

η₂= B(nα)².

В состоянии равновесия η₁= η₂

А(1-α)n= B(nα)²,

откуда:

.

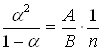Полученная формула выражает закон Оствальда, показывающий, как зависит коэффициент диссоциации α от концентрации раствора n.

Если ввести в электролит два электрода (металлических или угольных), соединенных с полюсами источника постоянного напряжения, и создать постоянное внешнее электрическое поле, то под действием электрических сил ионы в растворе придут в направленное движение. К аноду будут двигаться отрицатель­ные ионы (анионы), к катоду — положительные ионы (катионы).

Достигнув электродов, ионы разряжаются: анионы отдают аноду свои избыточные электроны, катионы восстанавливаются на катоде. Например, молекулы медного купороса CuSO₄ диссоциируют при растворении на положительные ионы Си⁺⁺ и отрицательные ионы SO₄^{- -} . Кроме ионов Си⁺⁺ и ионов SO₄^{- -}, раствор содержит также водородные (Н ⁺ ) и гидроксильные (ОН^-) ионы воды.

Ионы меди Си⁺⁺ разряжаются легче, чем ионы водорода Н⁺, поэтому при прохождении тока на катоде будет происходить выделение меди

Cu⁺⁺ + 2e = Cu.

Ионы SO₄^{- -} —труднее разряжаются, чем ионы ОН^-. Поэтому при прохождении тока у анода разряжаются ионы гидроксила и выделяется кислород

2ОН^--2е = Н₂О +О, 2О → О₂

Ионы SO₄^{- -}  — с ионами Н⁺ образуют у анода раствор серной кислоты

Иначе протекает процесс, если анод изготовлен из меди. В этом случае разряд ионов происходит только у катода; у анода же, наоборот, ионы металла переходят в раствор.

Объяснить это можно тем, что атомы меди Си теряют элек­троны легче, чем ионы ОН^-, в этом случае вместо выделения кислорода будет происходить переход с анода в раствор ионов Cu^{+ +}

Си-2е = Си^{+ +} .

Следовательно, электролиз CuSO₄ при медном аноде сводится к переносу меди с анода на катод. В то же время количество медного купороса в растворе остается неизменным. Прохождение постоянного электрического тока через электролиты сопровож­дается выделением составных частей этих веществ на электродах. Это явление называется электролизом.

Явление электролиза было тщательно исследовано Фарадеем, который установил на опыте два основных закона электролиза:

Согласно первому закону Фарадея, масса m вещества, выделившаяся на каком-либо из электродов, пропорциональна величине заряда q, прошедшего через электролит:

m = kq, (1)

где k – электрохимический эквивалент, различный для различных веществ.

Второй закон Фарадея утверждает, что электрохимический эквивалент пропорционален химическому эквиваленту данного вещества:

, (2)

где А – атомная масса, Z – валентность вещества, С – коэффициент пропорциональности, имеющий одно и то же значение для всех веществ.

Оба закона Фарадея можно выразить одной формулой. Подставляя выражение (2) для k в (1) и обозначая 1/С= F, находим:

 (3)

Величина F называется числом Фарадея. Число Фарадея F численно равно величине заряда , при прохождении которого через электролит на электроде выделяется один грамм-эквивалент вещества. Из формул (1) и (3):

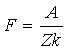. (4)

Известно, что в одной грамм-молекуле А любого вещества содержится одинаковое число атомов N, равное числу Авогадро N_A, а заряд одновалентного иона численно равен заряду электрона. Поэтому заряд электрона может быть вычислен по формуле:

e = F/N_A (5)

В электролитах носители заряда образуются независимо от электрического тока. Заряд положительных ионов в каждом объеме электролита равен заряду отрицательных ионов и поэтому объемный заряд в электролитах равен нулю. Вдали от электродов концентрация ионов (положительных и отрицательных) одинакова в разных точках электролита, вследствие этого градиент концентрации ионов внутри электролитов равен нулю и диффузия ионов не играет роли в образовании тока. При включении электрического поля на хаотическое тепловое движение ионов накладывается упорядоченное движение - положительных ионов в направлении поля, отрицательных – против направления поля.

 Плотность тока, создаваемая дрейфом положительных ионов равна:

,

где n₊- концентрация положительных ионов, e – заряд иона, υ₊- дрейфовая скорость положительных ионов. Аналогично для плотности тока отрицательных ионов можно написать:

.

Полная плотность тока :

Концентрации положительных и отрицательных ионов в электролитах одинаковы.

,

где α – коэффициент диссоциации, n –число молекул в единице объема электролита. Скорости ионов можно выразить через их подвижности и напряженность электрического поля в электролите:

, (6)

где b – подвижность ионов, равная скорости ионов в поле с напряженностью, равной единице. Например, подвижность ионов K⁺, Na⁺, Cl^-, NO^-₃ в водных растворах имеют вели­чину порядка 10 ^-3 см² /(Bc) Поэтому:

Плотность тока оказывается пропорциональной напряженности поля, а следовательно, для электролитов, так же как и для металлов, справедлив закон Ома. Удельная электропроводность электролита равна:

.

Она тем больше, чем выше коэффициент диссоциации α (чем больше концентрация ионов nα) и чем выше подвижность ионов b+ и b-.

Погружение металла или диэлектрика в электролит сопровождается появлением на границе их соприкосновения двойного электрического слоя толщиной в несколько характерных молекулярных расстояний r_m. Граница двойного слоя со стороны жидкости не резкая, а диффузная. Между жидкостью и твердым телом возникает скачок потенциала. Напряженность поля внутри двойного слоя определяется контактирующими веществами и может достигать больших значений.

При продавливании электролита через капилляр или пористую перегородку некоторая часть заряда двойного электрического слоя на расстояниях больших 2r_m-3r_m от поверхности твердого тела может двигаться в направлении движения жидкости. Приближенная теория была разработана Смолуховским (1903г). В соответствии с этой теорией движение электролита вдоль капилляра под действием электрического поля и возникновение электрического поля при продавливании электролита через капилляр представляют собой взаимно обратные явления.

Под действием поля Е электролит в капилляре или пористой перегородке движется со скоростью u, определяемой соотношением

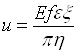, (7)

где η и ε - вязкость и диэлектрическая проницаемость раствора соответственно, f – числовой коэффициент, зависящий от размеров, проводимости материала капилляра и от концентрации ионов, образующих двойной электрический слой. Обычно 0<f<0,25; ξ - электрокинетический потенциал, т.е. часть разности потенциалов двойного электрического слоя, перемещающегося относительно твердого тела. Соотношение (7) позволяет оценить разность потенциалов, возникающую при продавливании электролита через пористую перегородку. Следует при этом учитывать, что u – скорость электролита не в центральной, а в пристеночной части капилляра.

Смещение ∆x иона за счет диффузии за время t определяется выражением

, (8).

Характерные значения D (коэффициента диффузии) для указанных выше ионов в водных растворах составляют 10^-5 см²/с.

Если диффузия происходит в электрическом поле, то подвижность и коэффициент диффузии связаны соотношением

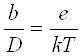 , (9)

где е – заряд электрона, k- постоянная Больцмана, Т – температура в Кельвинах (К).

Экспериментальная установка

 

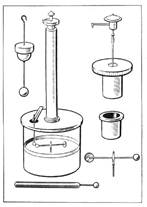
Экспериментальная установка состоит из двух частей. Для определения числа Фарадея и заряда электрона используется стеклянный сосуд, наполненный раство­ром CuSO₄ с двумя угольнымиэлектродами, подсоединенными к источнику тока (рис.1)

Для определения коэффициента диффузии, подвижности и скорости ионов используется плоская камера (рис. 2) , которая заполняется водным раствором нитрата калия (KNO₃) малой концентрации. Вместо камеры можно использовать смоченную в этом растворе фильтровальную бумагу или ткань, аккуратно разложенную на плоском изоляторе. При подаче напряжения между плоскими металлическими электродами, положенными в камеру или на бумагу (ткань) возникает электрический ток.

 

Проведение эксперимента

 

1.  Определить массу m₁ одного из угольных электродов на технических весах.

2.  Собрать цепь по рис. 1, подключив взвешенный электрод к минусу источника питания.

3.  Включить источник питания, установив с помощью реостата ток в цепи 1,5 А. Засечь время.

4.  Пропустить ток в течение 30-40 минут, поддерживая его постоянным при помощи реостата.

5.  Выключить источник тока. Вынуть катод, просушить, определить его массу m₂.

6.  Определить массу выделившегося вещества m = m₂ – m₁ .

7.  Используя формулу (1) вычислить величину электрохимического эквивалента k.

8.  По формуле (4) найти число Фарадея, подставляя значение k в г/Кл, Z=2, A = 63,54 г.

9.  По формуле (5) вычислить заряд электрона в СИ.

10.  Предварительно подготовленную ткань по размерам установки опустить в слабый раствор электролита KNO₃. Разложить ткань на установке так, чтобы не было пузырьков воздуха. Закрепить металло-графитовые электроды.

11.  Собрать цепь по рис. 2.

12.  Нанести на ткань одну каплю перманганата калия пипеткой между электро­дами Одновременно включить секундомер.

13.  Через 1-2 минуты выключить секундомер. Измерить смешение пятна ∆x

14.  Используя (8) рассчитать коэффициент диффузии D₁.

15.  Включить источник питания. Установить ток в цепи 120-150 mA.

16.  Нанести на ткань две капли перманганата калия пипеткой между электродами отдельно от первой и друг от друга, одновременно включить секундомер.

17.  Через 30-40 минут, выключить одновременно секундомер и источник питания.

18.  Измерить смешение пятна, ∆x₂ за время t₂,

19.  Используя формулу (8) рассчитать коэф­фициент диффузии D₂.

20.  Определить D по формуле : D=D2-D1

21.  Подставляя D в формулу (9) рассчитайте подвижность ионов MnO₄

22.  Найденное значение подвижности иона b подставить в формулу (6), рассчи­тать скорость движения ионов.

 

Контрольные вопросы

 

1.  Проводники первого и второго рода. Механизм их электропроводности.

2.  Что такое электрохимический эквивалент? Физический смысл электрохимического эквивалента.

3.  В чем заключается физический смысл числа Фарадея?

4.  Закон Ома для электролитов.

5.  Сопротивление электролитов и его физический смысл.

6.  Диссоциация. Рекомбинация. Закон Оствальда.

7.  Электролиз. Законы Фарадея для электролиза.

8.  Методика определения заряда электрона и числа Фарадея.

Литература, рекомендуемая к лабораторной работе:

 

1.  Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.

2.  Калашников С.Г. Электричество. – М.: Наука, 1977.

3.  Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.

4.  Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.

5.  Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.

6.  Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.

7.  Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.

8.  Рублев Ю.В., Куценко А.Н., Кортнев А.В. Практикум по электричеству. – М.: Высшая школа, 1971.

9.  Кортнев А.В., Рублев Ю.В., Куценко А.Н.. Практикум по физике. – М.: Высшая школа, 1965.

ЛАБОРАТОРНАЯ РАБОТА № 9

ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКИХ СВОЙСТВ

СЕГНЕТОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛОВ

Цель работы Исследование зависимости поляризованности сегнетоэлектриков от напряженности электрического поля при различных температурах

 

Идея эксперимента

 

В эксперименте производятся исследования диэлектрической проницаемости сегнетоэлектрика, подтверждающие соответствие температурной зависимости диэлектрической проницаемости сегнетоэлектрика закону Кюри-Вейсса.

 

Теоретическая часть

 

При помещении диэлектрика во внешнее электрическое поле, он поляризуется, т.е. приобретает отличный от нуля дипольный момент

P_v=∑p_i ,

где p_i - дипольный момент одной молекулы. Для количественного описания поляризации диэлектрика пользуются векторной величиной –поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:

P=p_v/V.

Из опыта следует, что для большого класса диэлектриков (за исключением сегнетоэлектриков) поляризованность P линейно зависит от напряженности поля E. Если диэлектрик изотропный и E не слишком велик, то

P=ǽε₀Е,

где ǽ - диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика, ǽ - величина безразмерная, притом всегда больше нуля и для большинства диэлектриков составляет несколько единиц. Например, для спирта ǽ=25, для воды – 80.

ǽ= ε-1,

где ε – диэлектрическая проницаемость среды.

Сегнетоэлектриками называются полярные диэлектрики, которые в определенном интервале температур спонтанно поляризованы, т.е. обладают поляризованностью при отсутствии электрического поля. На границах интервала температур сегнетоэлектрик в результате фазового перехода превращается в полярный диэлектрик.

Сегнетоэлектрики характеризуются чрезвычайно большим значением диэлектрической проницаемости, порядка 10⁴ (в то время как диэлектрическая проницаемость, например, дистиллированной воды равна 81). Величина поляризованности Р нелинейно и неоднозначно зависит от напряженности электрического поля Е. Сегнетоэлектрики способны проявлять свойство диэлектрического гистерезиса, то есть их поляризованность Р определяется не только величиной напряженности Е поля в данный момент времени, но и зависит от предыстории образца. Это явление полностью аналогично явлению ферромагнитного гистерезиса. Свое название сегнетоэлектрики получили от сегнетовой соли (NaKC₄H₄O₆´4H₂O), на которой впервые были обнаружены описанные выше свойства. В настоящее время известно более ста чистых сегнетоэлектриков. Среди них наиболее известным является титанат бария (BaTiO₃). Если изначально сегнетоэлектрик не был поляризован, то по мере роста напряженности внешнего поля, в которое он помещается, вектор поляризации Р увеличивается, что описывается основной кривой поляризации (участок ОА, рис.1). В достаточно сильных полях процесс поляризации достигает насыщения (Р= const). Если теперь начинать уменьшать напряженность поля, то поляризация начнет убывать, но зависимость P=f(E) теперь

 будет описываться участком кривой АВ. В результате при Е=0 сегнетоэлектрик будет обладать некоторой остаточной поляризацией Р_ост ¹ 0. Чтобы полностью деполяризовать сегнетоэлектрик, необходимо, изменив направление внешнего поля, увеличивать его напряженность до некоторой величины Е_с  (участок ВС кривой поляризации). Величина Е_сназывается коэрцитивной силой. Если продолжать увеличивать напряженность поля в направлении обратном к первоначальному, то сегнетоэлектрик вновь начнет поляризоваться до насыщения, но уже в обратном направлении (участок СD). Дальнейший ход кривой симметричен первоначальному участку АСD. Таким образом, график зависимости поляризованности от напряженности внешнего поля имеет вид петли, которую называют петлей гистерезиса.

Зависимость диэлектрической проницаемости сегнетоэлектрика от температуры характеризуется наличием максимума при достижении температуры Т_к, называемой температурой Кюри (рис.2). Выше температуры Т_к , характерной для каждого сегнетоэлектрика, его сегнетоэлектрические свойства исчезают и он превращается в обычный полярный диэлектрик

В некоторых случаях имеются две точки Кюри – сегнетоэлектрические свойства исчезают и при понижении температуры. Например, у сегнетовой соли имеются две точки Кюри, характеризуемые температурами 24ºС и -18ºС. Таких сегнетоэлектриков сравнительно немного. В области (Т>Т_к) зависимость ǽ от температуры описывается формулой

ǽ=А/(Т-Т₀) , (1)

где А – константа, Т₀ - температура Кюри-Вейсса, близкая к температуре Кюри. Закон, выражаемый формулой 1, называется законом Кюри-Вейсса.

Среди сегнетоэлектрических кристаллов различают две группы: сегнетоэлектрики с водородными связями (сегнетова соль, NaNO₃и др.), ориентация дипольных моментов в которых связана с поворотом молекул в пространстве; сегнетоэлектрики кислородно-октаэдрического типа (BaTiO₃ и др.), возникновение спонтанной поляризации которых сопровождается деформацией (растяжением) молекул.

Эти группы различаются значением константы А в законе Кюри-Вейсса и соотношением между Т₀ и Т_к. Для первой группы характерны значения константы А в диапазоне (1-5)×10³ К и Т₀=Т_к. Для второй группы константа А лежит в диапазоне (1-3)×10⁵ К, Т₀ примерно на 10° ниже, чем Т_к.

Спонтанная поляризация является источником очень больших электрических полей. Вокруг макроскопического объема сегнетоэлектрика, поляризованного спонтанно в некотором направлении, возникает электрическое поле большой энергии. Такое состояние энергетически невыгодно. Система стремится перейти в такое состояние, чтобы , с одной стороны, существовала спонтанная поляризация, а с другой стороны, энергия была бы минимальной. Это может осуществиться в результате разделения объема сегнетоэлектрика на малые области , в каждой из которых имеется спонтанная поляризация в некотором определенном направлении, различным для различных областей. При этом средняя поляризованность всего объема равна нулю, поэтому напряженность внешнего электрического поля, порождаемого этим объемом, близка к нулю. Малые области со спонтанной поляризацией называются диэлектрическими доменами или просто доменами. Таким образом, неполяризованный сегнетоэлектрик является совокупностью доменов с беспорядочно ориентированными спонтанными поляризованностями. Энергетически выгодно уменьшение объемов доменов, но этому процессу препятствует фактор, связанный с наличием поверхностной энергии на границе между соседними доменами. С уменьшением объемов доменов увеличивается суммарная поверхность границ, что ведет к увеличению поверхностной энергии, поэтому объемы доменов могут уменьшаться лишь до определенных пределов порядка тысяч межмолекулярных расстояний.

Процесс изменения поляризованности сегнетоэлектрика во внешнем электрическом поле состоит в переориентации дипольных моментов отдельных доменов в изменении объемов и движении границ между доменами.

Сегнетоэлектрики получили широкое применение в науке и технике. Например, на их основе получены конденсаторы с зависящей от температуры емкостью, так называемых варикондов.

 

Экспериментальная установка

 

Общий вид экспериментальной установки представлен на рис. 3, схема которой приведена на рис. 4. Образец представляет собой небольшой диск из сегнетоэлектрика с посеребренными поверхностями – вариконд 1.

Диэлектрическая проницаемость e исследуемого сегнетоэлектрика рассчитывается по измерениям емкости конденсатора С₁:

 (2)

Для температурных исследований образец помещается в нагреватель 2, питание которого осуществляется от сети. Скорость нагрева можно регулировать. Температура сегнетоэлектрика измеряется с помощью дифференциальной термопары 3 подключенной к милливольтметру 5, с пределом измерения 10 мВ. Контрольный спай термопары погружен в калориметр с таящим льдом 4. Градуировочная кривая термопары дана в приложении к прибору. Для измерения емкости вариконда используется измеритель иммитанса Е 7-15 6, внешний вид которого приведен на рис. 5.

Для проведения измерения достаточно подключить исследуемый образец к зажимам и установить нужный режим измерения. Нажатием кнопки «Параметр» установить прибор в режим измерения LC.

Для визуализации процесса используется электронный осциллограф ЭО.

Тумблером вида работ можно переключать схему на измерения и визуализацию.

 

Проведение эксперимента.

 

1.  Собрать цепь по схеме на рис. 3

2.  Переведите тумблер вида работ на визуализацию.

·  К клеммам ГЗ подключить звуковой генератор (600 Ом)

·  Подключить осциллограф ЭО.

·  Подать напряжение на установку и получить на экране осциллографа петлю гистерезиса.

3.  Переведите тумблер вида работ на работу с измерительным прибором.

·  Разарретировать милливольтметр. При необходимости с помощью корректора установить стрелку (зайчик) прибора на ноль.

·  Нагреватель установки при выполнении этого задания должен быть отключен.

·  Заполнить колотым льдом или снегом сосуд, в который погружается контрольный спай термопары. Лед должен быть таящим, для чего в сосуд можно добавить воды, чтобы получить смесь воды и льда. После этого милливольтметр должен показывать наличие термоЭДС (» 0,9 мВ).

·  Для электропитания внешних приборов можно использовать розетки, закрепленные на панели прибора.

4.  Температурные измерения лучше проводить при остывании сегнетоэлектрика. Этим обеспечивается более равномерный режим изменения температуры. Поэтому включите нагреватель и прогрейте сегнетоэлектрик до 110-120⁰С. Для определения температуры образца пользуйтесь градуировкой термопары.

5.  Выключите нагреватель. С уменьшением температуры емкость вариконда начинает изменяться. Необходимо снимать показания измерительного прибора (емкость вариконда С) в соответствии с показаниями милливольтметра вплоть до остывания образца до комнатной температуры.

6.  Заполните таблицу. Пересчитайте термоЭДС в температуру по шкале Цельсия. По формуле 2 рассчитайте величину диэлектрической проницаемости вариконда для каждой температуры.

7.  Постройте график зависимости диэлектрической проницаемости сегнетоэлектрика от температуры e=f(t) и по максимальному значению диэлектрической проницаемости определите точку Кюри для данного вида сегнетоэлектрика t_kи Т_к.

8.  Постройте график зависимости 1/e от абсолютной температуры 1/e = f(T) в области Т>Т_к. В соответствии формулой (1) этот график график представляет собой прямую линию:

По величине углового коэффициента найдите значение константы А в законе Кюри-Вейсса, а по точке пересечения прямой с осью ординат определите температуру Т₀. По порядку величины А и по соотношению между Т_к и Т₀сделайте вывод о типе сегнетоэлектрика, используемого в работе.

Примечания:

Данные схемы: R₁=1,5 кОм, R₂ = 100 кОм, С₀ = 10 мФ

Частота измерения: n = 300 Гц

Размеры сегнетоэлектрика: толщина d = 1 мм, диаметр D = 20 мм.

Чувствительность осциллографа по горизонтальной оси: U_x = 1В/дел.

Чувствительность осциллографа по вертикальной оси: U_y = 0,5 В/дел

Градуировка термопары 26,042 град/мВ

№ п/п	Показание миливольтметра, мВ	t°C
1	0,9	23,44
2	1,0	26,04
3	1,1	28,64
4	1,2	31,25
5	1,3	33,85
6	1,4	36,46
7	1,5	39,06
8	1,6	41,66
9	1,7	44,27
10	1,8	48,87
11	1,9	49,48
12	2,0	52,08
13	2,1	54,68
14	2,2	57,29
15	2,3	59,89
16	2,4	62,50
17	2,5	65,10
18	2,6	67,70
19	2,7	70,31
20	2,8	72,91
21	2,9	75,52
22	3,0	78,12
23	3,1	80,72
24	3,2	83,33
25	3,3	85,93
26	3,4	88,54
27	3,5	91,14
28	3,6	93,74
29	3,7	96,35
30	3,8	98,95
31	3,9	101,56
32	4,0	104,16

Контрольные вопросы

 

1.  Поляризация диэлектриков.

2.  Электронная теория поляризованного диэлектрика. Диэлектрическая проницаемость и диэлектрическая восприимчивость.

3.  Сегнетоэлектрики и их свойства.

4.  Диэлектрический гистерезис в сегнетоэлектриках, петля гистерезиса, точка Кюри.

5.  Как получить петлю гистерезиса на экране осциллографа.

6.  Природа сегнетоэлектрических свойств.

7.  Практическое применение сегнетоэлектриков.

8.  Описание экспериментальной установки и теория данного метода.

Литература, рекомендуемая к лабораторной работе:

 

1.  Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.

2.  Калашников С.Г. Электричество. – М.: Наука, 1977.

3.  Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.

4.  Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.

5.  Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.

6.  Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.

7.  Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.

8.  Рублев Ю.В., Куценко А.Н., Кортнев А.В. Практикум по электричеству. – М.: Высшая школа, 1971.

9.  Кортнев А.В., Рублев Ю.В., Куценко А.Н.. Практикум по физике. – М.: Высшая школа, 1965.

10.  Руководство к лабораторным занятиям по физике. Под редакцией Л.Л. Гольдина, - М.: Наука, 1983.

ЛАБОРАТОРНАЯ РАБОТА № 10

ИЗУЧЕНИЕ МАГНИТНЫХ ПОЛЕЙ

 

Цель работы:

 

Ознакомление с основными количественными характеристиками магнитных полей и методами их измерения. Определение горизонтальной составляющей индукции магнитного поля Земли с помощью тангенс- гальванометра.

 

Идея эксперимента:

 

В случае простейших конфигураций (прямой ток, тороид, бесконечной длины соленоид) значение напряженности магнитного поля легко находится с помощью теоремы о циркуляции Н, в более сложных случаях (соленоид конечной длины и др.) расчет Н затруднителен. Поэтому в ряде случаев удобнее экспериментально определить В, а затем рассчитать Н. Величину магнитной индукции В можно измерить различными способами или непосредственно прибором, называемым тесламетром (рис 4.)

 

Теоретическая часть

 

Экспериментально установлено, что в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Магнитное поле в данной точке может быть охарактеризовано вектором магнитной индукции В и вектором напряженности Н, которые связаны соотношением

В= μμ₀Н

где μ₀= 4π· 10^-7 Гн/м - магнитная постоянная, μ – магнитная проницаемость вещества, показывающая во сколько раз магнитная индукция в данной среде больше магнитной индукции в вакууме.

Магнитное поле обладает следующими свойствами:

·  магнитное поле действует только на движущиеся в этом поле электрические заряды:

·  магнитное поле подчиняется принципу суперпозиции В=∑В_i

·  магнитное поле является вихревым, т.е. линии магнитной индукции всегда замкнуты и охватывают проводники с током.

Количественно магнитные поля можно рассчитать по закону Био-Савара-Лапласа:

,

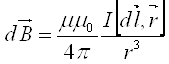где I - сила тока, dl – вектор, по модулю равный длине элемента проводника и совпадающий по направлению с током, r –радиус вектор, проведенный из элемента проводника dl в точку поля, в которой определяется В.

 Магнетизм Земли.

экватор

 Земля представляет собой огромный шаровой магнит. Хотя магнетизм Земли в течение уже нескольких тысячелетий использовался для определения сторон света с помощью магнитных стрелок, лишь в 1600 г. Уильям Гильберт научно доказал, что Земля – магнитный диполь. Строгую теорию геомагнетизма и методы магнитных измерений разработали в 30-е годы XIX века Карл Гаусс и Вильгельм Вебер.

В любой точке пространства, окружающего Землю, обнаруживается действие магнитных сил. Форма силовых линий магнитного поля Земли показана на рис.1 Северный магнитный полюс Земли находится в южном полушарии и имеет координаты 78° ю. ш. и 111° в. д., а южный магнитный полюс располагается в северном полушарии и имеет координаты 78° с. ш. и 69° з. д.. Эти значения непостоянны, так как со временем магнитные полюсы и ось меняют своё положение. Из сказанного следует, что магнитные полюса планеты смещены относительно географических полюсов более чем на 2000 км каждый. Это расстояние с годами возрастает по неизвестным науке причинам (в 1600 году оно составляло всего 1300 км).

Угол между горизонтальной составляющей вектора В и плоскостью географического меридиана называется магнитным склонением α и измеряется при помощи деклинаторов. В результате неоднородности земного магнитного поля его вектор индукции на экваторе направлен строго горизонтально, на магнитных полюсах – вертикально, а на всех остальных широтах – под некоторым углом к горизонту. Этот угол называется магнитным наклонением θ, которое измеряется посредством инклинаторов. Существование магнитного наклонения приводит к тому, что северный полюс магнитной стрелки, подвешенной в северном полушарии, располагается несколько ниже южного полюса, а в южном полушарии – наоборот (на глаз это незаметно). Такую ориентацию можно описать векторной суммой горизонтальной и вертикальной составляющих вектора индукции магнитного поля Земли (рис. 2). Вертикальную составляющую этого поля измеряют при помощи упомянутого выше инклинатора, а горизонтальную – при помощи тангенс-гальванометра. В стрелочном инклинаторе главной частью является магнитная стрелка с горизонтальной осью, проходящей через центр тяжести стрелки. Если вертикальную плоскость качания стрелки совместить с плоскостью магнитного меридиана, магнитная ось стрелки устанавливается по направлению вектора напряженности магнитного поля. Магнитное наклонение отсчитывается по вертикальному кругу с делениями. Более точные индукционные инклинаторы позволяют измерить наклонение с точностью до 0,1΄. В таком приборе индукционная катушка вращается вокруг оси, лежащей в плоскости ее витков. Прибор дает возможность ориентировать ось в любом направлении. Если она не совпадает с вектором напряженности магнитного поля Земли, то магнитный поток сквозь контур катушки при ее вращении меняется, и в ней индуцируется эдс. При совпадении оси вращения с направлением вектора напряженности поток сквозь ее контур остается постоянным, эдс не индуцируется, и включенный в цепь катушки чувствительный гальванометр не дает отклонений. Угол между горизонтальной плоскостью и осью катушки при отсутствии отклонений в гальванометре отсчитывается по вертикальному кругу, соединенному с осью катушки. Точные измерения показали, что в настоящее время горизонтальная составляющая вектора магнитной индукции B на поверхности планеты принимает значения от 0 до 41 мкТл, а полный вектор индукции B₀ изменяется в пределах от +62 до –73 мкТл.

 Магнитное поле Земли меняется и во времени. В настоящее время магнитное поле планеты убывает примерно на 1% каждые 10 лет.

 

Экспериментальная установка

Тангенс-гальванометр представляет собой короткую катушку большого диаметра, точно в центре которой располагается буссоль (компас). Размеры стрелки буссоли должны быть очень малы, что позволяет считать величину магнитного поля тока, действующего на концы стрелки, равной величине поля в центре кругового тока. По этой же причине катушка прибора должна быть как можно короче и как можно большего диаметра. Обмотка катушки представляет собой определённое число N витков медного провода и несколько отводов, сделанных через равное количество витков. Каждый отвод припаивается к отдельному гнезду на панели прибора, рядом с которым указывается соответствующее число витков. Перед началом измерений плоскость катушки тангенс-гальванометра располагают в плоскости магнитного меридиана планеты, после чего по обмотке прибора пропускают электрический ток. В результате стрелка оказывается под воздействием одновременно двух взаимно перпендикулярных полей: горизонтальной составляющей магнитного поля Земли В_г и поля В_I кругового тока катушки тангенс-гальванометра. При этом стрелка буссоли устанавливается вдоль вектора магнитной индукции результирующего поля.

.

Отсюда:

. (1)

Если катушка прибора содержит n витков, то индукция магнитного поля тока в центре катушки может быть определена по формуле:

, (2)

где R – радиус катушки тангенс-гальванометра. Таким образом, с учётом (1) и (2), получаем:

. (3)

Относительная погрешность определения величины В_г по формуле (3) определяется суммой:

. (4)

Таким образом, измерения горизонтальной составляющей магнитного поля Земли целесообразно производить при α = 45°, так как в этом случае, согласно (4), ошибка, связанная с неточностью определения угла α, будет минимальной. При этом выражение (3) упрощается:

. (5)

 

Проведение эксперимента

 

Определение горизонтальной составляющей магнитного поля Земли.