Изучите электроизмерительные приборы, используемые в работе, и запишите их паспортные данные
Аналогично определите чувствительность вертикально отклоняющих пластин, подавая напряжение на клеммы У
Построить график зависимости lnR=f(1/T), откладывая значения 1/Т по горизонтальной оси, a In R - по вертикальной
Собрать схему по рис. 2. Включать схему в цепь только с разрешения преподавателя!
Соберите цепь по схеме, указанной на рис. 3
Включить в сеть измеритель магнитной индукции (тесламетр, рис. 4). При необходимости провести установку нуля тесламетра
Метод магнитной фокусировки
Газоразрядную трубку расположите так, чтобы электронный пучок был направлен параллельно виткам катушек, при этом светящийся пучок примет вид кольца;
Для каждого значения тока вычислить значения Н и В
Поменять полярность источника, увеличивая обратный ток, перевести образец снова в насыщенное состояние
По формуле (13) вычислить индуктивность L катушки, подставляя в неё значения R и <Z>
Построить график
зависимости логарифмического декремента затухания от сопротивления контура
Навигация
Газоразрядную трубку расположите так, чтобы электронный пучок был направлен параллельно виткам катушек, при этом светящийся пучок примет вид кольца;
Электричество и магнетизм
189451
знак
18
таблиц
0
изображений
4. Газоразрядную трубку расположите так, чтобы электронный пучок был направлен параллельно виткам катушек, при этом светящийся пучок примет вид кольца;
5. Измерьте радиус кольца с помощью приспособления, состоящего из полупроводникового лазера и специального измерительного устройства, обеспечивающего перемещение луча лазера в двух взаимно перпендикулярных направлениях. Для этого направляющую пластину, вдоль которой перемещается лазер, установите строго параллельно плоскости кольца, при этом луч лазера будет направлен перпендикулярно этой плоскости. Перемещайте лазер с помощью микрометрической подачи, так чтобы его луч поочередно пересекал кольцо в точках, находящихся на концах его диаметра. Для более удобного совмещения точек пересечения лазером кольца и экрана, установленного по другую сторону колбы, лазер снабжен выступом (“мушкой”) на конце его цилиндрического корпуса. Измерения проведите несколько раз и найдите среднее значение радиуса кольца;
6. Измерьте радиус катушек Гельмгольца;
7. Данные измерений занесите в таблицу 2 и определите значение удельного заряда электрона по формуле (10);
8. Оцените погрешность полученных результатов.
Примечание: вектор магнитной индукции определяют с помощью измерителя индукции или по формуле:
, (13)
где 
- сила тока в катушках, А, 
– = 445 число витков, 
– радиус катушек,
Гн/м - магнитная постоянная.
Таблица 2
| N | U,В | r, м | I,A | R, м | N | B,Тл | e/m |
Контрольные вопросы
1. Движение заряженных частиц в электромагнитном поле.
2. Сила Лоренца, правило определения направления силы Лоренца.
3. Удельный заряд электрона и методы его определения.
4. Магнетрон. Метод определения удельного заряда с помощью магнетрона.
5. Определение удельного заряда по методу магнитной фокусировки.
6. Определение удельного заряда с помощью газоразрядной трубки.
7. Вывести формулы для определения удельного заряда методом магнетрона и газоразрядной трубки.
8. Вывести формулу для определения удельного заряда методом магнитной фокусировки.
9. Что такое сбросовая характеристика и как по ней определяется критический ток?
Литература, рекомендуемая к лабораторной работе:
1. Калашников С.Г. Электричество. – М.: Наука, 1977.
2. Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.
3. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.
4. Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.
5. Иродов И.Е. Электромагнетизм. Основные законы. –М.- С.-П.: Физматлит Невский диалект, 2001
6. Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.
7. Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.
8. Физический практикум. Электричество. Под редакцией В.И. Ивероновой. – М.: Наука, 1968.
9. Кортнев А.В., Рублев Ю.В., Куценко А.Н.. Практикум по физике. – М.: Высшая школа, 1965.
10. Руководство к лабораторным занятиям по физике. Под редакцией Л.Л. Гольдина, - М.: Наука, 1983.
ЛАБОРАТОРНАЯ РАБОТА №12
ПОЛУЧЕНИЕ КРИВОЙ НАМАГНИЧИВАНИЯ И ПЕТЛИ ГИСТЕРЕЗИСА С ПОМОЩЬЮ ОСЦИЛЛОГРАФА
Цель работы:
Получить экспериментальную зависимость магнитной индукции от напряженности магнитного поля, определить коэрцитивную силу, остаточную индукцию и построить график зависимости магнитной проницаемости от напряжённости магнитного поля.
Идея эксперимента:
Исследуемым веществом является железо, из которого изготовлен тороид с двумя обмотками. Индукция магнитного поля внутри полого тороида, равна:
, (1)
где n1 – число витков на один сантиметр длины первичной обмотки, I1 – ток, подаваемый на первичную обмотку тороида. Магнитная индукция связана с напряженностью соотношением:
(2)
Из формулы (1) и (2) получаем, что напряженность магнитного поля
,
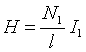(3)
где N1 – полное число витков первичной обмотки, l- длина средней линии тороида При прохождении переменного тока по первичной обмотке тороида во вторичной обмотке наводится э.д.с. индукции
,
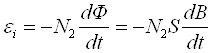где S - площадь сечения тороида, N2 - число витков во вторичной обмотке, В - индукция в образце.
Чтобы получить на экране осциллографа петлю гистерезиса, нужно на
горизонтально отклоняющие пластины подать напряжение Ux, пропорциональное напряженности Н магнитного поля в образце, а на вертикально отклоняющие пластины - напряжение Uy, пропорциональное магнитной индукции В. За один период синусоидального изменения тока след электронного луча на экране опишет полную петлю гистерезиса, а за каждый последующий период в точности её повторит. Поэтому на экране будет видна неподвижная петля гистерезиса. Изменяя напряжённость поля Н, можно получить на экране последовательно ряд различных по своей площади частных петель гистерезиса. Верхняя точка петли гистерезиса находится на кривой намагничивания. Следовательно, для построения начальной кривой намагничивания необходимо снять с осциллограмм координаты вершин nx и nyпетель гистерезиса, а значения Н и В вычислить по формулам (4), (5).
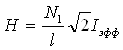, (4)
где Iэфф - эффективное значение тока, измеряемое амперметром (а на экране осциллографа мы видим амплитудное значение Н);
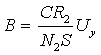, (5)
где Uy- амплитудное значение напряжения, определяемое с помощью осциллографа по положению калиброванного указателя УСИЛЕНИЕ У (вольт/дел.).
Теоретическая часть
Всякое вещество является магнетиком, т.е. оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Для характеристики магнитных свойств разных веществ вводят понятие магнитной восприимчивости χ, определяющей величину намагничения единицы объема вещества. В зависимости от знака и величины магнитной восприимчивости все магнетики разделяют на три группы: 1. диамагнетики, у которых χ отрицательна и мала по абсолютной величине; 2. парамагнетики, у которых χ тоже невелика, но положительна; 3. ферромагнетики, у которых χ положительна и достигает очень больших значений. Кроме того, в отличие от диа- и парамагнетиков, для которых χ постоянна, магнитная восприимчивость ферромагнетиков является функцией напряженности магнитного поля.
Кривая намагничивания.
Характерной особенностью ферромагнетиков является сложная нелинейная зависимость между индукцией В и напряженностью Н. Эта зависимость была установлена А.Г.Столетовым на примере железа. Зависимость индукции В от напряженности магнитного поля Н ферромагнетика имеет вид, показанный на рис. 1 Индукция сначала быстро увеличивается, но по мере намагничивания ферромагнетика, ее нарастание замедляется. По значениям индукции В и напряженности поля Н можно определить намагничение магнетика 
(магнитный момент единицы объема). Характер зависимости I(H) для ферромагнетиков изображен на рис.2. Намагничение J, подобно индукции, сначала быстро возрастает, но затем наступает магнитное насыщение, при котором намагничение достигает некоторого
максимального значения Js и практически перестает зависеть от напряженности поля.
Вследствие нелинейной зависимости B(H) магнитная проницаемость μ =B/ μ0H зависит от напряженности магнитного поля. Кривая зависимости μ (H) (рис. 3) возрастает с увеличением поля от начального значения до некоторой максимальной величины μmax, но затем, после прохождения через максимум, μ уменьшается и асимтотически стремится к значению очень му к нице.
Магнитная восприимчивость ферромагнетика χ =J/H оказывается также непостоянной и зависящей от напряженности поля. Она имеет максимум и при больших полях асимтотически стремится к значению близкому к нулю.
Гистерезис
Положим, что мы намагничиваем первоначально ненамагниченный ферромагнетик и, поместив его внутрь намагничивающей катушки, увеличиваем магнитное поле внутри магнетика от нуля до некоторого значения H1 (рис. 4). Значение индукции в магнетике будет определяться отрезком О1 кривой индукции О1А и изобразится отрезком ординаты ОВ1. Если теперь вновь уменьшать магнитное поле, то уменьшение индукции будет изображаться уже не отрезком кривой индукции 1О, а кривой 1В’, и когда поле станет равным нулю, индукция будет равна не нулю, а ОВ'. Ферромагнетик в этом состоянии будет являться постоянным магнитом. Если, далее, изменить направление тока в намагничивающей катушке и перемагничивать образец в обратном направлении, то изменение индукции опишется отрезком кривой В' 2. При последующем изменении поля в обратном направлении индукция будет изменяться в соответствии с кривой В''1. При циклическом перемагничивании ферромагнетика изменение индукции в нем изобразится петлеобразной замкнутой кривой 1В'2В''1.
Мы видим, что значение индукции в ферромагнетике определяется не только существующим магнитным полем, но еще зависит от предыдущих состояний намагничивания.
Происходит своеобразное отставание изменения индукции от изменения напряженности поля. Это явление получило название магнитного гистерезиса, а указанная выше петлеобразная кривая зависимости В(Н) при циклическом перемагничивании называется петлей гистерезиса. Из кривых на рис.4 видно, что при устранении намагничивающего поля ферромагнетик сохраняет остаточное намагничение, причем внутри магнетика существует некоторая остаточная индукция В0 (рис. 4). Чтобы уничтожить это остаточное намагничение, внутри ферромагнетика необходимо создать определенное поле, направленное против первоначального намагничивающего поля, изображенного отрезком ОНк. Это поле называется задерживающей или коэрцитивной силой ферромагнетика.
Гистерезис зависит от состава ферромагнетика и его обработки. Для чистого мягкого железа, т.е. отожженного и затем медленно охлажденного, гистерезис выражен слабо и петля гистерезиса очень узка. У закаленной стали гистерезис значителен и петля гистерезиса широкая.
Температура Кюри
Способность ферромагнетиков намагничиваться различна при разных температурах, т.е. их магнитная восприимчивость зависит от температуры. При повышении температуры способность ферромагнетиков намагничиваться уменьшается. При этом падают значения их магнитной восприимчивости и проницаемости при любом значении магнитного поля, ослабляется гистерезис и уменьшается намагничение насыщения Js. При некоторой температуре Тк, называемой температурой Кюри, ферромагнитные свойства исчезают. Температура Кюри различна для разных ферромагнетиков. Например, для кобальта Тк=1323 К, для железа Тк=1043 К, для никеля – 633 К, для гадолиния – 290 К
При температурах выше температуры Кюри, ферромагнетик становится парамагнетиком. Зависимость магнитной восприимчивости χ от температуры для таких парамагнетиков подчиняется закону Кюри-Вейсса, который имеет вид:
,
где С – постоянная, зависящая от рода вещества, ТК – температура Кюри.
Экспериментальная установка
Для получения петли гистерезиса на экране осциллографа используется установка, схема которой приведена на рис. 5.
Первичная обмотка тороида питается от источника В-24 через сопротивление R1 переменным током I1 . Напряжение, подаваемое с резистора R1 на горизонтально отклоняющие пластины, с учётом формулы (3) равно
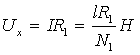
Таким образом, напряжение Ux, подаваемое на горизонтально отклоняющие пластины, пропорционально Н.
Чтобы напряжение, подаваемое на вертикальный вход осциллографа, было пропорционально индукции магнитного поля В, между вторичной обмоткой и осциллографом ставят интегрирующую цепочку из сопротивления R2, которое подбирается на магазине сопротивлений Р-33 и конденсатора С с магазина емкостей, удовлетворяющую условию, что R2>>1/ωC. Тогда сопротивлением конденсатора переменному току можно пренебречь, и сила тока I2 в цепи вторичной обмотки равна:
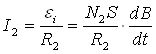. (6)
Напряжение на конденсаторе
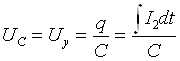(7)
Подставляя значение силы тока (6) в формулу (7), получим
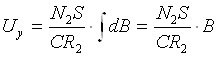
Таким образом, на вертикальный вход осциллографа подается напряжение Uy, пропорциональное значению магнитной индукции В.
Проведение эксперимента.
1. Собрать схему по рис. 2.
2. После проверки схемы включить осциллограф в сеть. Установить необходимую яркость и оптимальную резкость электронного луча. Вывести луч в центр координатной сетки.
3. Включить в сеть источник питания В-24 и подать переменное напряжение на первичную обмотку тороида
4. Изменяя ток, подаваемый с источника в первичную обмотку, подбирая сопротивление магазина R2 и регулируя усиление, по вертикали с помощью переключателя УСИЛЕНИЕ У, получить на экране петлю гистерезиса, которая имела бы участок насыщения и занимала всю координатную сетку. Зарисовать полученную петлю.
5. Записать показания амперметра и координаты nx и nyвершины петли гистерезиса. Определить напряжение Uy. Для этого показание переключателя УСИЛЕНИЕ У умножить на координату ny (дел) с учетом коэффициентом усиления осциллографа.
6. По формулам (4) и (5) вычислить магнитную индукцию В и напряжённость поля Н, соответствующие вершине петли гистерезиса.
7. Уменьшая подаваемое напряжение, постепенно стянуть петлю до минимума, измеряя при этом не менее 10 раз величину тока и соответствующие координаты nx и ny.
Похожие работы
... , хотя ему уже придавали иной смысл, нежели тот, который вкладывал в него Кулон.Введение понятия потенциалав электростатику Открытие закона Кулона было очень важным шагом в развитии учения об электричестве и магнетизме. Это был первый физический закон, выражающий количественные соотношения между физическими величинами в учении об электричестве и магнетизме. С помощью этого закона можно было ...
... самоиндукции и экстратоки замыкания и размыкания. Открытие явления электромагнитной индукции сразу же приобрело огромное научное и практическое значение; оно легло в основу электротехники. Работам Фарадея в области электричества положило начало исследование так называемых электромагнитных вращений. Из серии опытов Эрстеда, Араго, Био, Савара, проведенных в 1820 г., стало известно не только об ...
... в магнитном поле компасной стрелки в нем появляются токи, которые создают свое магнитное поле. Взаимодействие двух магнитных полей и дает «магнетизм вращения». «Теперь, – записал в своей рабочей тетради Фарадей, – когда мы знаем о существовании этих токов, явления, открытые Араго, можно объяснить, не приписывая их тому, что в меди образуется полюс, противоположный приближающемуся». Диск и магнит ...
... термин «электрический ток», понятие о направлении электрического тока и за полтора века предсказал возникновение науки об общих закономерностях процесса управления, связи и организованных системах – кибернетики. Ньютон электричества Звездный час в жизни Ампера наступил в сентябре 1820 г., когда он впервые узнал об открытии датским физиком Г. Х. Эрстедом (1819) действия электрического тока на ...
0 комментариев