Навигация
Вычисление пределов функций, производных и интегралов
Содержание
Задание № 1
Задание № 2
Задание № 3
Задание № 4
Задание № 5
Задание № 7
Задание № 8
Задача № 4
Задача № 5
Задача № 6
Список литературы
Задание № 1
3. б) Найти пределы функции:
![]()
Решение
Одна из основных теорем, на которой основано вычисление пределов:
Если существуют
![]() и
и ![]() , то:
, то: ![]()
![]()
![]()
Следовательно:
![]()
Ответ: предел функции
![]()
Задание № 2
3. б) Найти производную функции:
![]()
Решение
Воспользуемся правилом дифференцирования сложных функций:
Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.
Тогда
![]()
Применим это правило к заданной функции:
![]()
Ответ: ![]()
Задание № 3
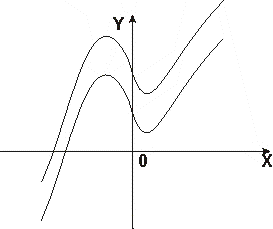
3. Исследовать функцию и построить ее график:
![]()
Решение
1. Найдем область определения функции:
D(y)=R
2. Исследуем функцию на четность и нечетность, на периодичность.
Условие четности: f(x)=f(-x)
Условие нечетности: f(-x)=-f(x)
при x=1: y=0
при x=-1: y=-4
Условия не выполняются, следовательно, функция не является четной и нечетной.
Периодической называется такая функция, значения которой не изменяются при прибавлении к аргументу некоторого (отличного от нуля) числа – периода функции.
Функция
![]()
не периодична.
3. Найдем промежутки знакопостоянства, выясним поведение функции на концах промежутков.
y=0 при ![]()
![]()
![]() ;
; ![]()
![]()
Следовательно, имеем три промежутка:
![]()
Определим знак на каждом промежутке:
при x= -1 y=-4 < 0
при x= 0,5 y=0,125 > 0
при x= 2 y=2 > 0
Тогда: для
![]() , для
, для ![]()
Рассмотрим поведение функции на концах промежутков:
![]()
![]()
![]()
4. Найдем промежутки монотонности функции, ее экстремумы.
Найдем производную функции:
![]()
![]()
при
![]() ,
, ![]()
- точки экстремума, они делят область определения функции на три промежутка:
![]()
Исследуемая функция в промежутке
![]() – возрастает
– возрастает
![]() – убывает
– убывает
![]() - возрастает
- возрастает
Похожие работы
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
... работа как прием обучения может входить почти во все методы обучения, воспитывать в учениках потребность самостоятельно добывать знания, умение творчески пользоваться объяснениями учителя, помощью товарищей, книгами, конспектами одна из важнейших целей нашей работы.ГЛАВА 2. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИЙ ПРИЁМЫ И МЕТОДЫ §1. Анализ программ и учебников «Алгебра, 7», «Алгебра, ...
... , которые содержат неизвестную функцию, её производные и аргументы. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется наивысший ...
... Строгое определение предела дается сначала для функций частного вида – последовательностей, а затем переносится на функции общего вида. На основе понятия предела определяются важнейшие понятия математического анализа – производная и интеграл. Предел последовательности Последовательностью называется функция, определенная на множестве натуральных чисел N = . Значения этой функции , N, называются ...

0 комментариев