Навигация
Найдем промежутки выпуклости графика функции, ее точки перегиба
5. Найдем промежутки выпуклости графика функции, ее точки перегиба.
Найдем вторую производную функции:
![]()
![]() при
при ![]() - точка перегиба
- точка перегиба
![]()
Для
![]()
![]() ,
,
следовательно, график функции на этом интервале выпуклый вверх.
Для
![]()
![]() ,
,
следовательно, график функции на этом интервале выпуклый вниз.
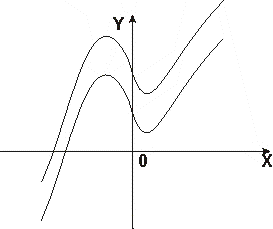
6. По полученным данным построим график функции.
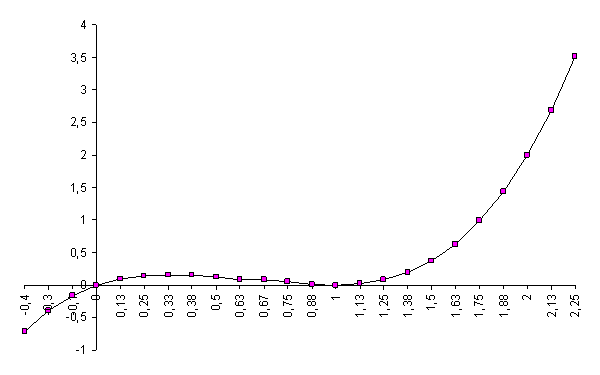
Рис. 3 График функции ![]()
Задание № 4
Найти интеграл:
3. 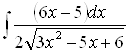
Решение
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают:
![]()
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Замена переменной в неопределенном интеграле производится с помощью подстановки:
![]()

Ответ: ![]() .
.
Задание № 5
Вычислить площадь фигуры, ограниченной линиями, используя определенный интеграл. Сделать чертеж.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение.
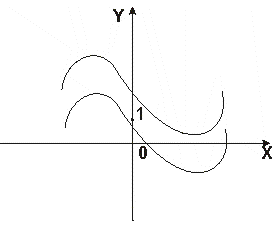
Построим график функции: ![]()
при х=-2: y = 12
при х=-1: y = 5
при х=0: y = 0
при х=1: y = -3
при х=2: y = -4
при х=3: y = -3
при х=4: y = 0
при х=5: y = 5
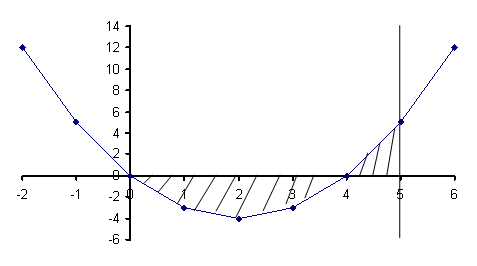
Рис. 1 График
Найдем точки пересечения графика функции с осью Оx:
![]()
![]()
![]()
![]()
![]()
Определим площадь полученной фигуры через определенный интеграл:
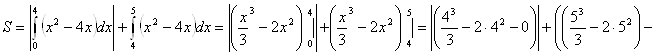
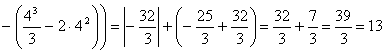 кв. ед.
кв. ед.
Ответ: площадь фигуры, ограниченной заданными линиями = 13 кв. ед.
Задание № 7.
Найти общее решение или общий интеграл дифференциального уравнения, решить задачу Коши для заданных начальных условий:
![]() ,
, ![]() при
при ![]()
Решение
Общий вид дифференциального уравнения: ![]()
Общим решением дифференциального уравнения первого порядка называется функция ![]() от переменной x и произвольной постоянной C, обращающая уравнение в тождество. Общее решение, записанное в неявном виде
от переменной x и произвольной постоянной C, обращающая уравнение в тождество. Общее решение, записанное в неявном виде ![]() , называется общим интегралом.
, называется общим интегралом.
Решение, полученное из общего при фиксированном значении С: ![]() , где
, где ![]() - фиксированное число, полученное при заданных начальных условиях
- фиксированное число, полученное при заданных начальных условиях ![]() , называется частным решением, или решением задач Коши.
, называется частным решением, или решением задач Коши.
Найдем общее решение или общий интеграл:
![]()
![]()
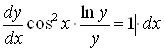

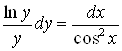

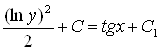
![]()
![]() -
-
общее решение дифференциального уравнения
Найдем частное решение для ![]() при
при ![]()
![]()
Получаем: ![]()
Ответ: ![]() - любое число.
- любое число.
Задание № 8
Найти вероятность случайного события.
Условие: Брошена игральная кость. Какова вероятность того, что выпадет нечетное число очков? Что выпадет шестерка»?
Решение.
Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
![]()
..................................................................................................................
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.
Обозначим в данной задаче выпадение нечетного числа – событие А, выпадение «шестерки» – событие В. На игральной кости шесть граней, очевидно, что на трех из них число нечетное, на одной – «шестерка».
Тогда в соответствии с записанными выше формулами получаем:
![]()
![]() .
.
Ответ: 1. вероятность выпадения нечетного числа равна ![]() ;
;
2. вероятность выпадения «шестерки» равна ![]() .
.
Методы вычислений и ЭВМ
Задача № 4.
Внедрение автоматизированного способа обработки информации снизило расходы на ее обработку с 238200 руб. до 50175 руб. Определите, на сколько процентов снизились расходы на обработку информации. Приведите рациональный алгоритм вычислений на МК.
Решение:
| Схема решения | Алгоритм | Результат |
| 238200 – 100 % 50175 – х %
|
| 21,064 % |
Задача № 5
Расходы на перевозку почты во II квартале уменьшились на 2,5 % по сравнению с I кварталом; в III квартале увеличились на 2,9 % по сравнению со II кварталом; IV квартале они вновь увеличились на 3,1 % по сравнению с III кварталом. Определите с точностью до 0,1 %, как изменились расходы в IV квартале по сравнению с I кварталом. Запишите рациональный алгоритм вычислений на МК.
Решение:
По условию задачи задано последовательное изменение начального показателя N=100 процентов на
Р1=2,5 %, Р2=2,9 %, Р3= 3,1 %.
Тогда:
Nn = 100(1-2,5/100)(1+2,9/100)(1+3,1/100) = 100(1-0,025)(1+0,029)(1+0,031) = 100*0,975*1,029*1,031 = 103,4 %
Алгоритм выполнения этого вычисления на МК:
100 – 2,5 % + 2,9 % + 3,1 %
Задача № 6
Бригаде монтажников за месяц начислено 16713 руб. Распределите заработную плату между членами бригады пропорционально следующим данным. Приведите рациональный алгоритм вычислений на МК, а также решение задачи с помощью табличного процессора (Excel, Super Calc и др.). Точность 0,01 руб.
| Табельный номер | Часовая тарифная ставка, руб | Отработано часов | К оплате, руб |
| 03 | 6,6 | 165 | |
| 04 | 8,8 | 72 | |
| 05 | 7,5 | 216 |
Алгоритм решения на МК:
6,6 * 165 М+
8,8 * 72 М+
7,5 * 216 М+
16713 /MR MR * 1089 = М+
C C 633,6 = М+
1620 = М+ MR
C
Решение задачи с помощью табличного процессора Excel:
1. Ввод названий граф документа:
| Адрес клетки | Вводимая строка |
| А1 | Табельный номер |
| А2 | 03 |
| А3 | 04 |
| А4 | 05 |
| В1 | Начислено, руб. (всего) |
| С1 | Часовая тарифная ставка, руб. |
| D1 | Отработано часов |
| Е1 | К оплате, руб. |
2. Ввод исходных данных:
| Адрес ячейки | Исходные данные |
| В2 | 16713 |
| С2 | 6,6 |
| С3 | 8,8 |
| С4 | 7,5 |
| D2 | 165 |
| D3 | 72 |
| D4 | 216 |
3. Ввод расчетных формул:
| Адрес ячейки | Исходные данные |
| F2 | С2*D2 |
| F5 | =СУММ(F2:F4) |
| E2 | $B$2/$F$5*F2 |
| E5 | =СУММ(Е2:Е4) |
4. Конечный результат:
| Табельный номер | Начислено, руб. (всего) | Часовая тарифная ставка, руб. | Отработано часов, ч. | К оплате, руб. | Ставка, руб. |
| 03 | 16713 | 6,6 | 165 | 5445,00 | 1089,00 |
| 04 | 8,8 | 72 | 3168,00 | 633,60 | |
| 05 | 7,5 | 216 | 8100,00 | 1620,00 | |
| 16713,00 | 3342,60 |
Список литературы
1. Выгодский М.Я. Справочник по высшей математике. – М.: АСТ, 2005. – 991 с.
2. Гусак А.А., Гусак Г.М., Бричкова Е.А. Справочник по высшей математике. – Минск. ТетраСистемс, 2004. – 640 с.
3. Гмурман В.Е. Теория вероятности и математическая статистика. – М.: Высшая школа, 1998. – 479 с.
4. Миносцев В.Б. Курс высшей математики. Часть 2. М. 2005. – 517 с.
5. Пономарев К.К. Курс высшей математики. Ч. 2. – М.: Инфра-С, 1974. – 520 с.
Похожие работы
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
... работа как прием обучения может входить почти во все методы обучения, воспитывать в учениках потребность самостоятельно добывать знания, умение творчески пользоваться объяснениями учителя, помощью товарищей, книгами, конспектами одна из важнейших целей нашей работы.ГЛАВА 2. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИЙ ПРИЁМЫ И МЕТОДЫ §1. Анализ программ и учебников «Алгебра, 7», «Алгебра, ...
... , которые содержат неизвестную функцию, её производные и аргументы. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется наивысший ...
... Строгое определение предела дается сначала для функций частного вида – последовательностей, а затем переносится на функции общего вида. На основе понятия предела определяются важнейшие понятия математического анализа – производная и интеграл. Предел последовательности Последовательностью называется функция, определенная на множестве натуральных чисел N = . Значения этой функции , N, называются ...

0 комментариев