Навигация
Решение задачи быстродействия симплекс-методом
2. Решение задачи быстродействия симплекс-методом
Дана система:
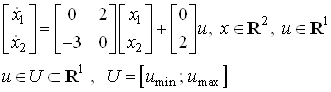 (3)
(3)
1. Проверим управляемость данной системы.
Запишем систему ДУ в матричном виде:
![]() ,
,
где 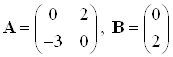 .
.
Данная система является стационарной, её порядок ![]() , поэтому матрица управляемости имеет вид:
, поэтому матрица управляемости имеет вид:
![]()
Найдем матрицу управляемости:

Ранг матрицы управляемости равен порядку системы, следовательно, данная система является управляемой.
![]() следовательно
следовательно ![]() .
.
Собственные числа матрицы ![]() найдем из уравнения
найдем из уравнения ![]() :
:
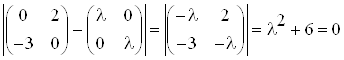
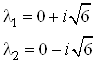
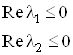
Действительные части собственных значений матрицы ![]() являются неположительными, следовательно, все условия управляемости выполнены.
являются неположительными, следовательно, все условия управляемости выполнены.
2. Ссылаясь на решение задачи быстродействия из ДЗ№2 по СУЛА «Решение задачи быстродействия» имеем:
Запишем зависимости ![]() ,
, ![]() , полученные при решении систем дифференциальных уравнений:
, полученные при решении систем дифференциальных уравнений:
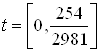 :
:
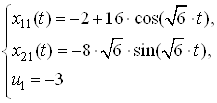
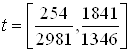 :
:

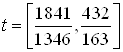 :
:
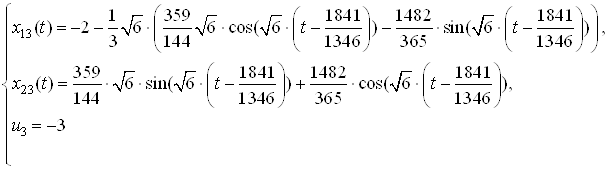
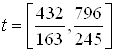 :
:
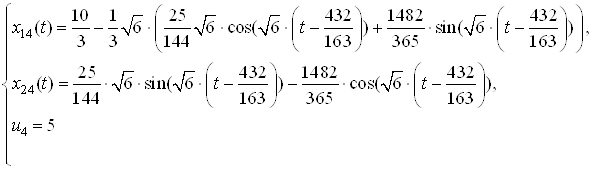
Перейдем к дискретной модели заданной системы. Имеем
![]() (4)
(4)
где ![]() шаг дискретизации и соответствующие матрицы
шаг дискретизации и соответствующие матрицы
 (5)
(5)
Пусть управление ограничено интервальным ограничением
![]() (6)
(6)
Тогда на ![]() шаге имеем
шаге имеем
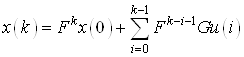 (7)
(7)
Известны начальная и конечная точки
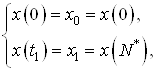
где ![]() – оптимальное число шагов в задаче быстродействия.
– оптимальное число шагов в задаче быстродействия.
Решается задача быстродействия
![]()
а) Формирование задачи быстродействия как задачи линейного программирования
Конечная точка ![]() в дискретной модели представлена в виде
в дискретной модели представлена в виде
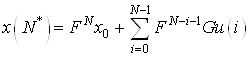 (8)
(8)
Получаем ![]() – равенств
– равенств
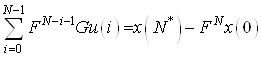 (9)
(9)
Для приведения ограничений (9) к канонической форме сделаем необходимое преобразование в правой и левой частях, чтобы правые части были неотрицательными (если правая часть меньше нуля, то домножаем на (-1) левую и правую части). Отметим проведенные изменения точкой в правом верхнем углу соответствующих векторов
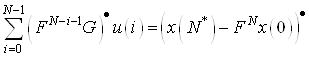 . (10)
. (10)
Для того чтобы получить необходимый допустимый базис для задачи линейного программирования, добавим формально остаточные искусственные переменные (![]() ). Таким образом, уравнения (10) представляются в виде
). Таким образом, уравнения (10) представляются в виде
 (11)
(11)
Так как текущее управление ![]() – управление имеет любой знак,
– управление имеет любой знак, ![]() то сделаем необходимую замену
то сделаем необходимую замену
![]()
Тогда уравнения (11) примут вид
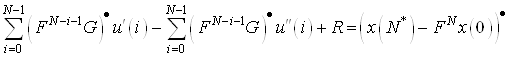 (12)
(12)
Введем остаточные переменные в ограничения на управление
![]()
![]()
 (13)
(13)
При объединении выражений (12) и (13) получаем ![]() ограничений.
ограничений.
Начальный допустимый базис состоит из остаточных и остаточных искусственных переменных
![]()
Формируем целевую функцию (по второму методу выбора начального допустимого базиса)
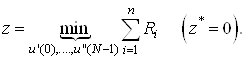 (14)
(14)
б) Решение задачи быстродействия
Предположим, что ![]() , где
, где ![]() – оптимальное число шагов. Так как значение
– оптимальное число шагов. Так как значение ![]() нам неизвестно (но
нам неизвестно (но ![]() известно точно), выбираем некоторое начальное
известно точно), выбираем некоторое начальное ![]() и решаем задачу линейного программирования (12)-(14).
и решаем задачу линейного программирования (12)-(14).
При этом
Общее число столбцов в симплекс-таблице: ![]()
Число базисных переменных: ![]()
Сформируем ![]() строку. Имеем
строку. Имеем
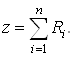
Выразим из уравнения (12) начальные базисные переменные ![]()
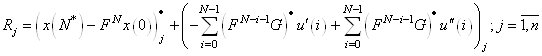
и подставим в целевую функцию. Получим ![]() – строку
– строку
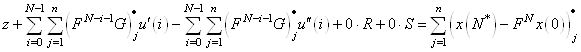 (15)
(15)
Решаем задачу (12) – (14) симплекс-методом.
В случае,
если ![]() ,
, ![]() – малое число
– малое число ![]()
иначе
1) если ![]() увеличить
увеличить ![]() и целое,рвернуться к первому шагу формирования задачи линейного программирования;
и целое,рвернуться к первому шагу формирования задачи линейного программирования;
2) если ![]() (не все управления будут равны предельным, могут быть, в том числе нулевые)),
(не все управления будут равны предельным, могут быть, в том числе нулевые)), ![]() , уменьшить
, уменьшить ![]() , вернуться к первому шагу формирования задачи линейного программирования.
, вернуться к первому шагу формирования задачи линейного программирования.
Решения данной задачи получено с помощью пакета Matlab 7.4 (скрипт SimplexMetod2.m): ![]()
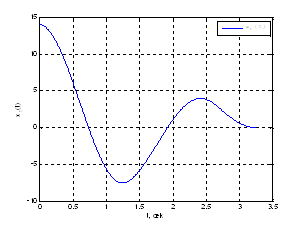
Рис. 14. График фазовой координаты ![]() .
.
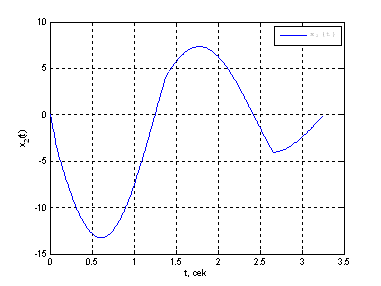
Рис. 15. График фазовой координаты ![]() .
.
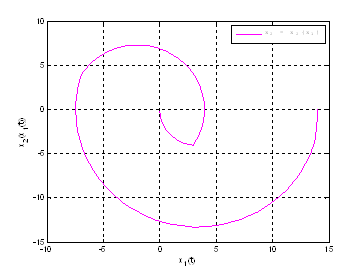
Рис. 16. График ![]() .
.
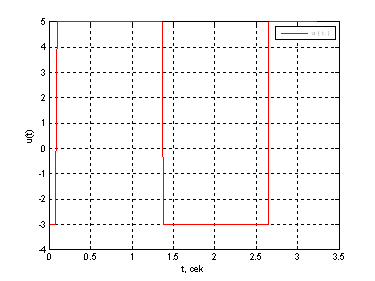
Рис. 17. График оптимального управления ![]() .
.
Выводы: Сравнивая полученные результаты с результатами полученными в ДЗ№2 по СУЛА, можно сделать вывод, что решения совпадают, с точностью до ![]() .
.
3. Оптимальная L – проблема моментов 3.1 Оптимальная L – проблема моментов в пространстве «вход-выход»
Укороченная система данного объекта имеет вид:
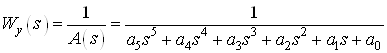 ,
,
где:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Полюса укороченной передаточной функции:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Заданы начальные и конечные условия:
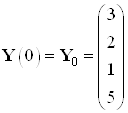 ,
, 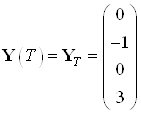 ,
, ![]() .
.
Для определения начальных и конечных условий для ![]() воспользуемся следующей формулой:
воспользуемся следующей формулой:
![]() ,
,
Где матрица ![]() имеет следующий вид
имеет следующий вид
 ,
,
где ![]() ,
, ![]() .
.
ИПФ укороченной системы:
![]()
Составим фундаментальную систему решений:
ФСР:  .
.
Составим матрицу ![]() .
.
![]() , где
, где ![]() – матрица Вронского
– матрица Вронского
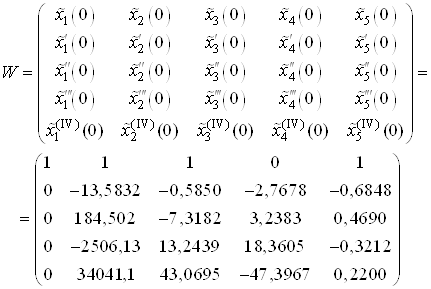
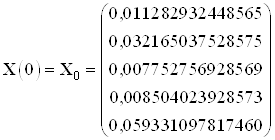 ,
,
Тогда
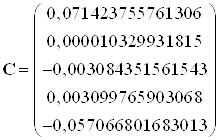 .
.
Составим моментные уравнения (связь между входом и выходом):
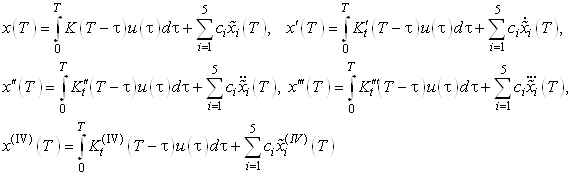
Моментные функции определяются по следующей формуле
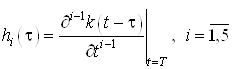
Составим моментные функции:
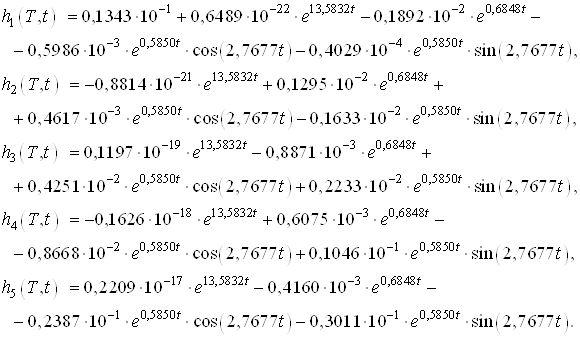
Найдем моменты по следующей формуле:
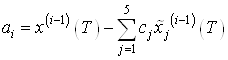 .
.
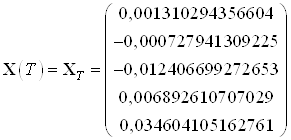
Числовое значение найденных моментов:
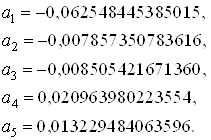
Составим функционал качества, который имеет следующий вид:
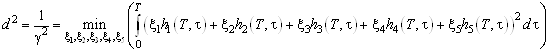
при условии, что :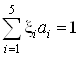 , т.е.
, т.е. ![]()
Выразим из данного условия ![]() , тогда получим следующее равенство:
, тогда получим следующее равенство:
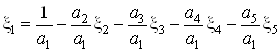 .
.
Подставляя полученное равенство в функционал и заменяя ![]() их правыми частями получаем
их правыми частями получаем
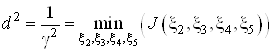
Найдем частные производные 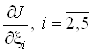 и приравняем их к нулю. Решая полученную систему уравнений, определяем оптимальные значения коэффициентов
и приравняем их к нулю. Решая полученную систему уравнений, определяем оптимальные значения коэффициентов ![]() , а
, а ![]() вычислим по формуле
вычислим по формуле
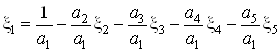 .
.
Т.о. имеем:
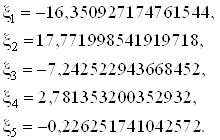
Минимальная энергия:
![]()
Найдем управление по следующей формуле:
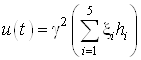
Тогда оптимальное управление
 .
.
3.2 Оптимальная L – проблема моментов в пространстве состояний
Система задана в виде:
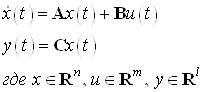
Решение ДУ имеет вид:
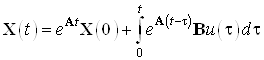 , при
, при ![]() имеем:
имеем:
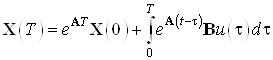 .
.
Составим моментные уравнения:
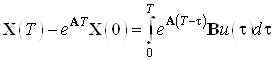
![]()
Подставляя необходимые данные в выше приведенные формулы, получим следующие моменты и моментные функции:
Числовое значение найденных моментов:
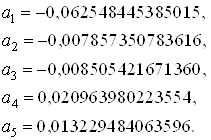
Моментные функции:
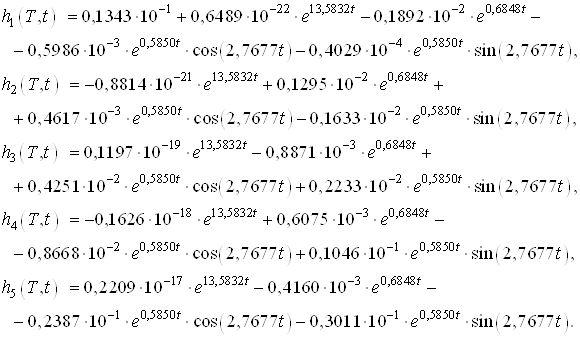
Заметим, что моменты и моментные функции совпадают с моментами и моментными функциями, найденными в пункте (а).
Из этого следует, что функционал, значения ![]() , управление и минимальная энергия будут иметь точно такие же числовые значения и аналитические выражения, как и в пункте (3.1).
, управление и минимальная энергия будут иметь точно такие же числовые значения и аналитические выражения, как и в пункте (3.1).
Оптимальное управление имеет вид:
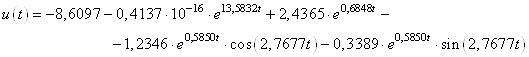
Проверим правильность полученного решения.
Эталонные значения координат в начальный и конечный момент времени:
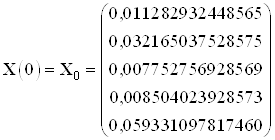 ,
, 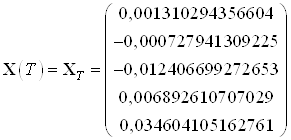
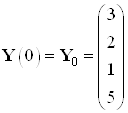 ,
, 
Найденные значения координат в начальный и конечный момент времени:
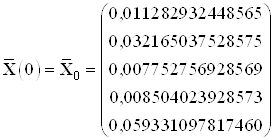 ,
, 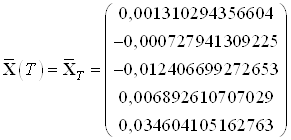
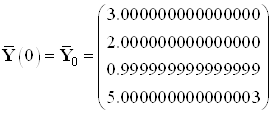 ,
, 
Вычислим погрешность полученных результатов:
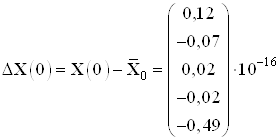 ,
, 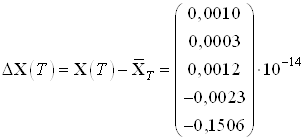
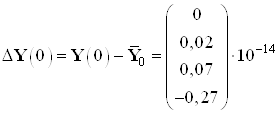 ,
, 
Ниже представлены графики полученного решения с помощью скрипта Optimal_L_problem_moments.m.
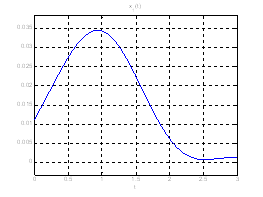
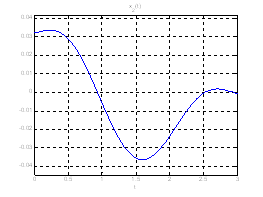
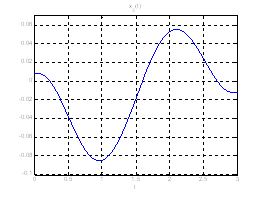
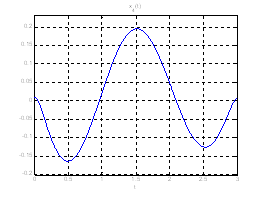
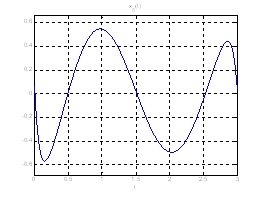
Рис. 18. Графики фазовых координат системы при переходе из ![]() в
в ![]() .
.
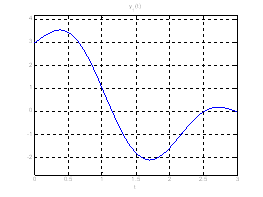
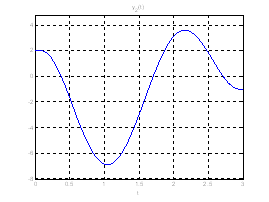
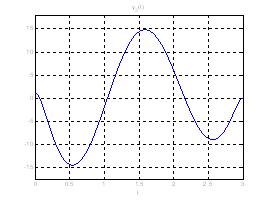
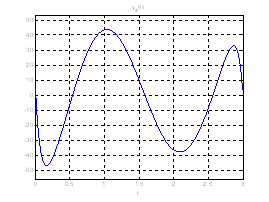
Рис. 19. Графики выходных координат системы при переходе из ![]() в
в ![]() .
.
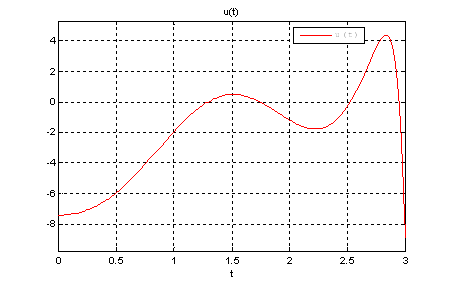
Рис.20. График оптимального управления ![]() .
.
Выводы: Задача перевода системы из начальной точки в конечную с помощью L-проблемы моментов в пространстве состояний и в пространстве вход-выход была решена с точностью до 12-го знака после запятой. Результаты, полученные при переводе системы из начальной точки в конечную, полностью совпадают.
4. Нахождение оптимального управления с использованием грамиана управляемости (критерий – минимизация энергии)
Система имеет вид:
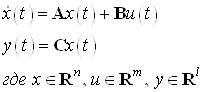
с начальными условиями:
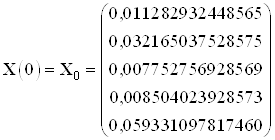 ,
, 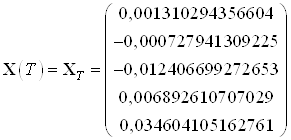
![]() .
.
Составим матрицу управляемости и проверим управляемость системы:
![]()

![]() .
.
Составим грамиан управляемости для данной системы:
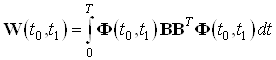
Найдем грамиан по формуле:
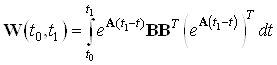

Тогда управление имеет вид:
![]() .
.
или
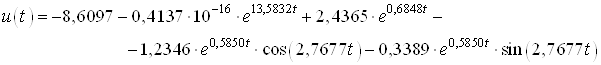
Ниже представлен график оптимального управления полученного с помощью скрипта Gramian_Uprav.m.:
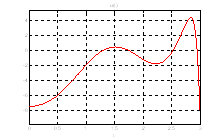
Рис.21. График оптимального управления ![]() .
.
Графики фазовых координат аналогичны, как и в оптимальной L – проблеме моментов.
Сравним управление, полученное в начальной и конечной точках в пунктах 3 и 4 соответственно:
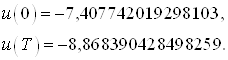 и
и 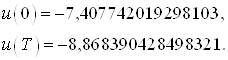
Выводы: Как видно, значения граничных управлений совпадают. А это значит, что задача перевода объекта из начального состояния в конечное решена с высокой степенью точности и с минимальной энергией.
Графическое сравнение оптимальных управлений из пунктов 3 и 4:
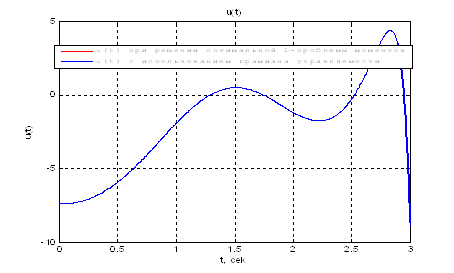
Рис.21. Сравнение графиков оптимального управления ![]() .
.
5. Аналитическое конструирование оптимальных регуляторов (АКОР) 5.1 Стабилизации объекта управления на полубесконечном интервале времени
Рассмотрим линейный объект управления, описываемый системой дифференциальных уравнений в нормальной форме
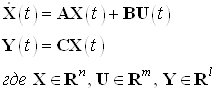
Необходимо получить закон управления
![]()
минимизирующий функционал вида
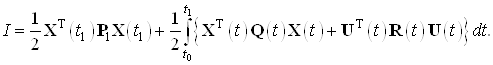
Начальные условия для заданной системы ![]()
Моменты времени ![]() фиксированы. Матрицы
фиксированы. Матрицы ![]() — симметричные неотрицательно определенные:
— симметричные неотрицательно определенные:
![]()
матрица ![]() — положительно определенная:
— положительно определенная:
![]()
Матричное дифференциальное уравнение Риккати имеет вид:
![]()
Если линейная стационарная система является полностью управляемой и наблюдаемой, то решение уравнения Риккати при ![]() стремится к установившемуся решению
стремится к установившемуся решению ![]() не зависящему от
не зависящему от ![]() и определяется следующим алгебраическим уравнением:
и определяется следующим алгебраическим уравнением:
![]()
В рассматриваемом случае весовые матрицы ![]() и
и ![]() в функционале не зависят от времени.
в функционале не зависят от времени.
Оптимальное значение функционала равно
![]()
и является квадратичной функцией от начальных значений отклонения вектора состояния.
Таким образом, получаем, что при ![]() оптимальное управление приобретает форму стационарной обратной связи по состоянию
оптимальное управление приобретает форму стационарной обратной связи по состоянию
![]()
где ![]() — решение алгебраического матричного уравнения Риккати.
— решение алгебраического матричного уравнения Риккати.
Похожие работы
... степеней свободы. Величину критерия Фишера (F-критерий) определяют по формуле: (должно быть). Значимость коэффициентов bi уравнения регрессии определяют по t-критерию (критерии Стьюдента): , . Идентификация объектов управления методом корреляционного анализа Метод корреляционного анализа используется для идентификации объектов управления в том случае, если входные и выходные ...
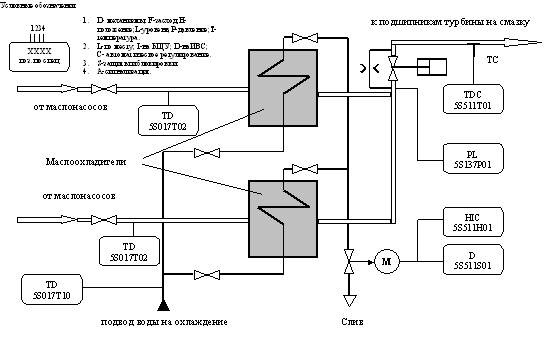
... : - по маслу 20кПа - по воде 20,1кПа Максимальное рабочее давление: - масла 0,5Мпа - воды 0,5МПа Функциональная схема системы регулирования температуры смазочного масла приведена на рис. 9. Она содержит два маслоохладителя параллельно ...
... проектирования. Целью проекта является создание программного продукта (ПП), основанного на математическом пакете MatLab, реализующего математическую модель системы управления, построенной на основе оптимального закона, для системы слежения РЛС. Данный проект можно отнести к научно-исследовательской работе, которая принадлежит к типу прикладных, направленных на решение научных проблем с целью ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
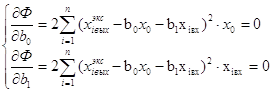
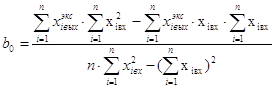
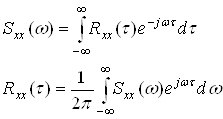




0 комментариев