В остальном данная задача аналогична задаче построения линейного сервомеханизма (пункт 5.5)

Решение задачи быстродействия симплекс-методом Решение алгебраического уравнения Риккати методом диагонализации В остальном данная задача аналогична задаче построения линейного сервомеханизма (пункт 5.5)

99279

знаков

таблиц

156

изображений

Решение алгебраического уравнения Риккати методом диагонализации

4. В остальном данная задача аналогична задаче построения линейного сервомеханизма (пункт 5.5).

Используя скрипт AKOR_slegenie_so_skolz_intervalami_Modern, получили следующие результаты:

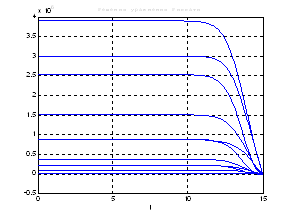
Рис.50. Графики решения уравнения Риккати.

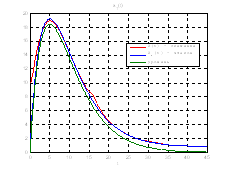
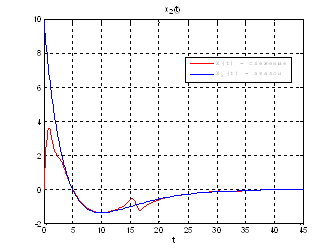
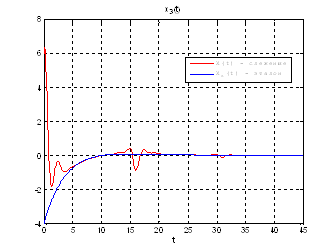
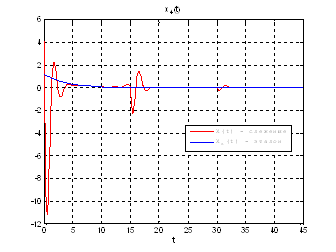
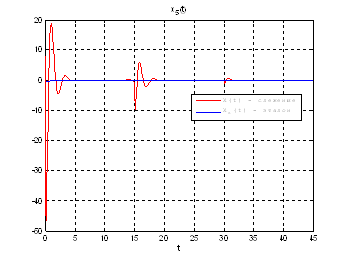
Рис.51. Графики фазовых координат.

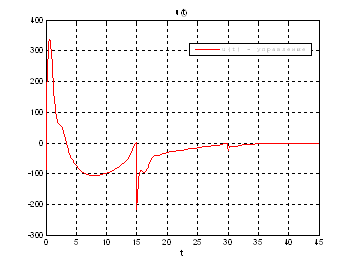
Рис.52. График управления.

Выводы: при сравнении полученных результатов, можно сказать, что различия в фазовых координатах при наличии трех участков и при наличии одного участка несущественные. Если сравнивать скорость вычислений и используемые ресурсы, то скорость увеличивается почти в 3 раза, а памяти требуется в 3 раза меньше для решения поставленной задачи. В точках соединения участков наблюдаются скачки, связанные с тем, что требуется значительные затраты на управление, но для первой координаты этот скачок незначительный.

6. Синтез наблюдателя полного порядка

Наблюдателями называются динамические устройства, которые позволяют по известному входному и выходному сигналу системы управления получить оценку вектора состояния. Причем ошибка восстановления .

Система задана в виде:

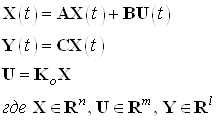
Начальные условия для заданной системы .

Матрицы заданы в пункте 5.1.1.

Весовые матрицы и имеют следующий вид:

, .

Построим наблюдатель полного порядка и получим значения наблюдаемых координат таких, что:

В качестве начальных условий для наблюдателя выберем нулевые н.у.:

Ранг матрицы наблюдаемости:

- матрица

наблюдаемости.

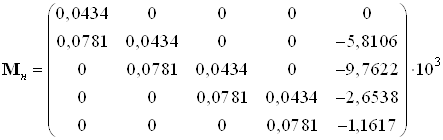Т. е. система является наблюдаемой.

Коэффициенты регулятора:

тогда

Собственные значения матрицы :

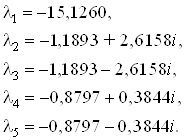
Коэффициенты наблюдателя выберем из условия того, чтобы наблюдатель был устойчивым, и ближайший к началу координат корень матрицы лежал в 3 – 5 раз левее, чем наиболее быстрый корень матрицы . Выберем корни матрицы

Коэффициенты матрицы наблюдателя:

Используя скрипт Sintez_nablyud_polnogo_poryadka, получили следующие результаты:

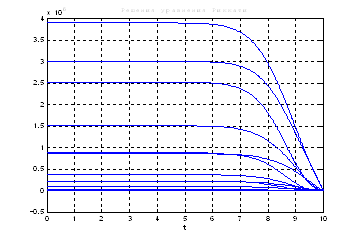
Рис.53. Графики решения уравнения Риккати.

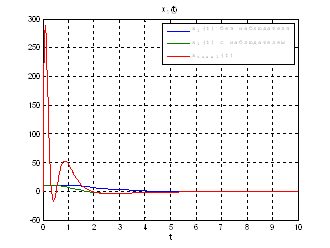
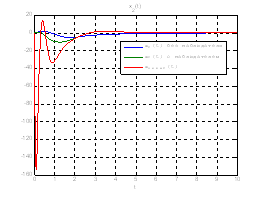
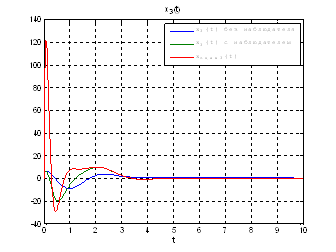
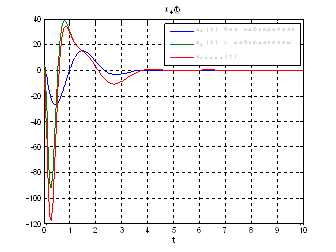
Рис.54. Графики фазовых координат.

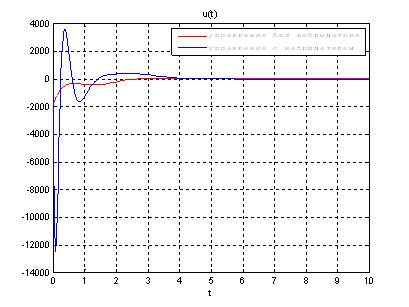
Рис.55. Графики управлений.

Выводы: Так как система является полностью наблюдаема и полностью управляема, то спектр матрицы может располагаться произвольно. Перемещая собственные значения матрицы левее, относительно собственных значений матрицы мы улучшаем динамику системы, однако, наблюдатель становится более чувствителен к шумам.

Литература

1. Методы классической и современной теории автоматического управления: Учебник в 5 – и т. Т.4: Теория оптимизации систем автоматического управления / Под ред. Н.Д. Егупова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 748 с.

2. Краснощёченко В.И.: Методическое пособие: «Методы теории оптимального управления».

Приложение.

PlotTimeFrHaract.m

clc

clear all

close all

b1 = 9;

b0 = 5;

a4 = 0.1153;

a3 = 1.78;

a2 = 3.92;

a1 = 14.42;

a0 = 8.583;

% syms s w

% W_s_chislit = b1 * s + b0;

% W_s_znamen = s * (a4 * s^4 + a3 * s^3 + a2 * s^2 + a1 * s + a0);

% W_s_obj = W_s_chislit/W_s_znamen;

%A_w = collect(simplify(abs(subs(W_s_obj, s, i*w))))

%----------------------Построение АЧХ-------------------------------------%

figure('Name', '[0,10]');

w = 0 : 0.01 : 10;

A_w = sqrt((b0^2 + b1^2.*w.^2)./((-a1*w.^2+a3*w.^4).^2+(a0*w-a2*w.^3+a4*w.^5).^2));

plot(w,A_w,'k', 'LineWidth', 2);

grid on

xlabel('w')

ylabel('A(w)')

title('Function ACHX(w)')

%-------------------------------------------------------------------------%

r_ch = roots([b1 b0])

r_zn = roots([a4 a3 a2 a1 a0 0])

%----------------------Построение ФЧХ-------------------------------------%

figure('Name', '[0,100]');

w = 0 : 0.01 : 100;

fi_w = (atan(w/0.5556)-atan(w/0)-atan(w/13.5832)-atan((w-2.7677)/0.5850)...

-atan((w+2.7677)/0.5850) - atan(w/(0.6848)))*180/pi;

plot(w,fi_w, 'k', 'LineWidth', 2);

grid on

xlabel('w')

ylabel('fi(w)')

title('Function FCHX(w)')

%-------------------------------------------------------------------------%

%----------------------Построение АФЧХ------------------------------------%

figure('Name', '[0,100]');

w = 0 : 0.01 : 100;

A_w = sqrt((b0^2 + b1^2.*w.^2)./((-a1*w.^2+a3*w.^4).^2+(a0*w-a2*w.^3+a4*w.^5).^2));

fi_w = (atan(w/0.5556)-atan(w/0)-atan(w/13.5832)-atan((w-2.7677)/0.5850)...

-atan((w+2.7677)/0.5850) - atan(w/(0.6848)));

polar(fi_w,A_w, 'k');

grid on

xlabel('Re(W(jw))')

ylabel('Im(W(jw))')

title('Function AFCHX(fi_w,A_w)')

%-------------------------------------------------------------------------%

%----------------------Построение ЛАЧХ------------------------------------%

figure('Name', '[0,100]');

w = -100 : 0.01 : 100;

LA_w = 20*log(sqrt((b0^2 + b1^2.*w.^2)./((-a1*w.^2+a3*w.^4).^2+(a0*w-a2*w.^3+a4*w.^5).^2)));

plot(w,LA_w,'k', 'LineWidth', 2);

grid on

xlabel('w')

ylabel('L(w)')

title('Function L(w)')

%-------------------------------------------------------------------------%

%----------------------Построение ФАЧХ------------------------------------%

%-------------------------------------------------------------------------%

%----------------------Построение h(t)------------------------------------%

figure('Name', '[0,50]');

t = 0 : 0.01 : 50;

h_t = 0.0024 * exp(-13.5832.*t) - 0.2175 * exp(-0.6848.*t)...

+ 0.1452 * exp(-0.5850.*t).* cos(2.7677.*t)...

- 0.2217 * exp(-0.5850.*t).* sin(2.7677.*t)...

+ 0.5825 .* t + 0.0699;

plot(t,h_t, 'k', 'LineWidth', 2);

grid on

xlabel('t')

ylabel('h(t)')

title('Function h(t)')

%-------------------------------------------------------------------------%

%----------------------Построение k(t)------------------------------------%

figure('Name', '[0,50]');

t = 0 : 0.01 : 50;

k_t = - 0.0329 * exp(-13.5832.*t) + 0.1489 * exp(-0.6848.*t)...

- 0.6986 * exp(-0.5850.*t).* cos(2.7677.*t)...

- 0.2721 * exp(-0.5850.*t).* sin(2.7677.*t)...

+ 0.5826;

plot(t,k_t, 'k', 'LineWidth', 2);

grid on

xlabel('t')

ylabel('k(t)')

title('Function k(t)')

%-------------------------------------------------------------------------%

x1=tf([b1 b0],[a4 a3 a2 a1 a0 0]);

ltiview(x1)

ProstranstvoSostoyanii.m

clc

clear all

%format rational

b1 = 9;

b0 = 5;

a5 = 0.1153;

a4 = 1.78;

a3 = 3.92;

a2 = 14.42;

a1 = 8.583;

a0 = 0;

%1. Матрица Фробениуса

A=[0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0;

0 0 0 0 1;

0 -a1/a5 -a2/a5 -a3/a5 -a4/a5]

B=[0; 0; 0; 0; 1/a5]

C=[b0 b1 0 0 0]

%Проверка

syms s

W_s = collect(simplify(C*(s.*eye(5)-A)^(-1)*B),s)

pretty(W_s)

%2. Параллельная декомпозиция

b1 = b1/a5;

b0 = b0/a5;

s1 = 0;

s2 = -6615/487;

s3 = -1022/1747 + 4016/1451*i;

s4 = -1022/1747 - 4016/1451*i;

s5 = -415/606;

alfa = real(s3);

beta = imag(s3);

syms s A B C D E

W_s_etal = collect(((b1*s+b0)/((s-s1)*(s-s2)*((s+alfa)^2+beta^2)*(s-s5))),s)

%pretty(W_s_etal)

Slag_1 = simplify(collect(A*(s-s2)*((s+alfa)^2+beta^2)*(s-s5),s));

Slag_2 = simplify(collect(B*(s-s1)*((s+alfa)^2+beta^2)*(s-s5),s));

Slag_3 = simplify(collect(C*(s-s1)*((s+alfa)^2+beta^2)*(s-s2),s));

Slag_4 = simplify(collect((D*s+E)*(s-s1)*(s-s2)*(s-s5),s));

Chislit_W_s =collect(Slag_1 + Slag_2 + Slag_3 + Slag_4,s);

%Решение системы линейных уравнений

MS =double( [1 1 1 1 0;

6753029497/515578134 -513659/1058682 10560977/850789 4210795/295122 1;

77456808434995506239663107/126764366837761533378822144 1874500571398143988939141/260296441145300889894912 -3300780600401725219142291/418364246989311991349248 915075/98374 4210795/295122;

26189071674868424275768861465/253528733675523066757644288 2853037197681682345182805/520592882290601779789824 45476725452203201718998205/418364246989311991349248 0 915075/98374;

6290947020888109571128085025/84509577891841022252548096 0 0 0 0])

PCH = [0; 0; 0; b1; b0];

Koeff = MS^(-1)*PCH

%Проверка

MS*[Koeff(1);Koeff(2);Koeff(3);Koeff(4);Koeff(5)];

Slag_1 = simplify(collect(Koeff(1)*(s-s2)*((s+alfa)^2+beta^2)*(s-s5),s));

Slag_2 = simplify(collect(Koeff(2)*(s-s1)*((s+alfa)^2+beta^2)*(s-s5),s));

Slag_3 = simplify(collect(Koeff(3)*(s-s1)*((s+alfa)^2+beta^2)*(s-s2),s));

Slag_4 = simplify(collect((Koeff(4)*s+Koeff(5))*(s-s1)*(s-s2)*(s-s5),s));

Chislit_W_s =collect((Slag_1 + Slag_2 + Slag_3 + Slag_4),s);

Znamena_W_s = collect((s-s1)*(s-s2)*((s+alfa)^2+beta^2)*(s-s5),s);

W_s = collect(simplify(Koeff(1)/(s-s1)+Koeff(2)/(s-s2)+(Koeff(4)*s+Koeff(5))/((s+alfa)^2+beta^2)+Koeff(3)/(s-s5)),s)

pretty(W_s)

%Расчет матриц состояния

A = [s1 0 0 0 0;

0 s2 0 0 0 ;

0 0 0 1 0;

0 0 -(alfa^2+beta^2) -2*alfa 0;

0 0 0 0 s5]

B = [Koeff(1); Koeff(2); 0; 1; Koeff(3)]

C = [1 1 Koeff(5) Koeff(4) 1]

%Проверка

W_s = collect(simplify(C*(s.*eye(5)-A)^(-1)*B),s)

pretty(W_s)

%ВСЕ ПОДСЧИТАНО ВЕРНО!!!

SimplexMetod2.m

function SimplexMetod2

clc

clear all

close all

format short

% Матрицы системы

A = [0 2;

-3 0];

B = [0; 2];

% Координаты начальной и конечной точки

X_0 = [14; 0];

X_N = [0; 0];

% Ограничение на управление

u_m = -3;

u_p = 5;

eps = 1e-10;% погрешность сравнения с нулем

N = 195;% число шагов

%h = t1/N;% шаг дискретизации

h = 0.0162;

alfa = 1;

a = 0;

b = 0;

%t1 = 796/245;% время перехода в конечное состояние

n = size(A);

n = n(1);% порядок системы

% Нахождение матричного экспоненциала

syms s t

MatrEx = ilaplace((s*eye(n)-A)^(-1));

MatrEx_B = MatrEx*B;

% Вычисление матриц F и G

F = subs(MatrEx, t, h);

G = double(int(MatrEx_B, t, 0, h));

ФОРМИРОВАНИЕ ЗАДАЧИ БЫСТРОДЕЙСТВИЯ КАК ЗАДАЧИ

ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

for index = 1 : 1e+10

% Вычисление правой части

PravChast = X_N - F^N * X_0;

% Вычисление произведения F на G

FG = zeros(n, N);% формирование матрицы для хранения данных

for j = 1 : n

for i = 0 : N - 1

fg = F^(N-i-1) * G;

if PravChast(j) < 0

fg = -fg;

end

FG(j, i+1) = fg(j);

end

% Построение z-строки

z_stroka = zeros(1, 4*N+n+2);% формирование матрицы для хранения данных

% Первый элемент z-строки

z_stroka(1) = 1;

% Суммирование правых частей

for j = 1 : n

z_stroka(4*N+n+2) = z_stroka(4*N+n+2) + abs(PravChast(j));

end

% Формирование элементов z-строки между 1-м и последним элементами

%при 2N небазисных переменных, т.е. при управлениях

for i = 2 : 2 : 2 * N

for j = 1 : n

z_stroka(i) = z_stroka(i) + FG(j, i/2);

end

for j = 1 : n

z_stroka(i+1) = z_stroka(i+1) - FG(j, i/2);

end

% Формирование симплекс-таблицы

CT = zeros(n+2*N+1, 4*N+n+2);

% Построение симплекс-таблицы начиная с z-строки

CT(1,:) = z_stroka(1,:);

% Формирование R-строк в симплекс-таблице

for j = 2 : n + 1

% Формирование правой части в R-строках

CT(j, 4*N+n+2) = abs(PravChast(j-1));

% Формирование элементов R-строк между 1-м и последним элементами

%при 2N небазисных переменных, т.е. при управлениях

for i = 2 : 2 : 2 * N

CT(j, i) = FG(j-1, i/2);

CT(j, i+1) = -FG(j-1, i/2);

end

% Формирование S-строк в симплекс-таблице

l = 2;

for j = n + 2 : 2 : n + 2 * N + 1

% Формирование правой части в S-строках

CT(j, 4*N+n+2) = u_p;

CT(j+1, 4*N+n+2) = abs(u_m);

% Формирование элементов S-строк между 1-м и последним элементами

%при 2N небазисных переменных, т.е. при управлениях

CT(j, l : l+1) = [1 -1];

CT(j+1, l : l+1) = [-1 1];

l = l + 2;

end

% Формирование базиса в симплекс-таблице, т.е коэффициентов, стоящих при

%базисных переменных от 2N небазисных переменных до правой части (до 4*N+n+1)

CT(2 : n+2*N+1, 2*N+2 : 4*N+n+1) = eye(n+2*N, n+2*N);

РЕШЕНИЕ ЗАДАЧИ БЫСТРОДЕЙСТВИЯ

% Цикл смены базисных переменных

nn = size(find(CT(1,2:2*N+1) >= eps));

while nn > 0

[znach, N_stolb] = max(CT(1, 2 : 2*N+1));

N_stolb = N_stolb + 1; % т.к. при небазисн. перемен.

PravChast = CT(:, 4*N+n+2);

for j = 2 : n + 2 * N + 1

if CT(j, N_stolb) > 0

PravChast(j) = PravChast(j) / CT(j, N_stolb);

else

PravChast(j) = inf;

end

[znach, N_str] = min(PravChast(2 : n+2*N+1));

N_str = N_str + 1;

% Формирование матрицы перехода B

B = eye(n+2*N+1, n+2*N+1);

B(:, N_str) = CT(:, N_stolb);

% Обращение матрицы B

RE = B(N_str, N_str);

for j = 1 : n + 2 * N + 1

if j == N_str

B(j, N_str) = 1 / RE;

else

B(j, N_str) = -B(j, N_str) / RE;

end

%B = inv(B);

% Получение новой симплекс таблицы

CT = B * CT;

nn = size(find(CT(1,2:2*N+1) >= eps));

end

u = zeros(1,N);

% Формирование управления

for j = 2 : n + 2 * N + 1

for i = 2 : 2 * N + 1

if CT(j, i) >= eps

if mod(i, 2) < eps

u(i/2) = CT(j, 4*N+n+2);

else

u((i-1)/2) = -CT(j, 4*N+n+2);

end

% Формирование x1 и x2

X = zeros(n, N);

X(:, 1) = F * X_0 + G * u(1);

for i = 2 : N

X(:, i) = F * X(:, i-1) + G * u(i);

end

% Объединение с начальными условиями

X1 = [X_0(1) X(1, :)];

X2 = [X_0(2) X(2, :)];

% проверка на окончание выбора количества шагов

XX = [X_0 X];

% Вычисление нормы вектора состояния

normaXX = norm(XX(:,N))

% Вычисление значения переменной R

R = abs(X_N - F^N * X_0) - FG * u';

R = R';

z = sum(R);

% Погрешность приближения к точному решению

pogresh = 0.3;

if (normaXX < pogresh)

N_opt = N;

break;

else

if (z > h)

if a == 1

alfa = ceil(alfa/2);

end

N = N + alfa;

a = 0;

b = 1;

else

if b == 1

alfa = ceil(alfa/2);

end

N = N - alfa;

a = 1;

b = 0;

end

t_perevoda = N * h;

end

N_opt

t_perevoda

ОФОРМЛЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

В ГРАФИЧЕСКОМ ВИДЕ

% Построение графика x1(t);

figure(1)

t = (0 : 1 : length(X1)-1) * h;

plot(t, X1, 'b', 'LineWidth', 2);

hl=legend('x_1(t)');

set(hl, 'FontName', 'Courier');

xlabel('t, cek'); ylabel('x_1(t)');

grid on

% Построение графика x2(t);

figure(2)

t = (0 : 1 : length(X2)-1) * h;

plot(t, X2, 'b', 'LineWidth', 2);

hl=legend('x_2(t)');

set(hl, 'FontName', 'Courier');

xlabel('t, cek'); ylabel('x_2(t)');

grid on

% Построение графика x2 = x2(x1);

figure(3)

plot(X1, X2, 'm', 'LineWidth', 2);

hl=legend('x_2 = x_2(x_1)');

set(hl, 'FontName', 'Courier');

xlabel('x_1(t)'); ylabel('x_2(x_1(t))');

grid on

% Построение графика u(t)

figure(4)

t = (0 : 1 : length(u)-1) * h;

plot(t, u, 'r', 'LineWidth', 2);

hl=legend('u(t)');

set(hl, 'FontName', 'Courier');

xlabel('t, cek'); ylabel('u(t)');

grid on

Optimal_L_problem_moments.m

clc

close all

clear all

format long

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Порядок системы

poryadok = 5;

% Начальные и конечные условия относительно вектора Y

Y_0 = [3 2 1 5]';

Y_T = [0 -1 0 3]';

% Конечное время перехода

T = 3;

% Матрица перехода от Н.У. Y к Н.У. X

B_ = [b0 b1 0 0 0;

0 b0 b1 0 0;

0 0 b0 b1 0;

0 0 0 b0 b1];

% ------------------------------------------------------------------------%

% Начальные условия для упорядоченной системы

X_0 = B_' * inv(B_ * B_') * Y_0

X_T = B_' * inv(B_ * B_') * Y_T

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4]

B = [0; 0; 0; 0; 1]

C = [b0 b1 0 0 0]

% ------------------------------------------------------------------------%

% Вычисление матричной экспоненты

syms s t

MatrEx = simplify (vpa(ilaplace(inv(s*eye(5) - A)), 50))

% ------------------------------------------------------------------------%

RETURN = 1;

while RETURN == 1

disp('L - проблема моментов в пространстве вход-выход: 1')

disp('L - проблема моментов в пространстве состояний : 2')

reply = input('Выберете метод решения [1 или 2]: ', 's');

switch reply

case '1'

disp('L - проблема моментов в пространстве вход-выход')

% ------------------------L - проблема моментов---------------------------%

% ----------------------в пространстве вход-выход-------------------------%

% ------------------------------------------------------------------------%

% Передаточная функция

W_obj_s = 1/(a5*s^5 + a4*s^4 + a3*s^3 + a2*s^2 + a1*s + a0);

% Полюса передаточной функции

polyusa_TF = roots([a5 a4 a3 a2 a1 a0]);

% ИПФ

K_t = simplify (vpa (ilaplace(1 / (a5*s^5 + a4*s^4 + a3*s^3 + ...

a2*s^2 + a1*s + a0)),50))

% K_t = vpa(K_t,6)

% ------------------------------------------------------------------------%

% Составление матрицы Вронского

for i = 1 : poryadok

Matrix_Vron (i, 1) = diff (exp (polyusa_TF(1) *t), t, i - 1);

Matrix_Vron (i, 2) = diff (exp (polyusa_TF(2) *t), t, i - 1);

Matrix_Vron (i, 3) = diff (exp (real(polyusa_TF(3))*t) * ...

cos(imag(polyusa_TF(3))*t), t, i - 1);

Matrix_Vron (i, 4) = diff (exp (real(polyusa_TF(4))*t) * ...

sin(imag(polyusa_TF(4))*t), t, i - 1);

Matrix_Vron (i, 5) = diff (exp (polyusa_TF(5) *t), t, i - 1);

end

% Матрица Вронского при t = 0;

Matrix_Vron_t_0 = double(subs(Matrix_Vron,t,0));

% Матрица Вронского при t = T;

T = 3;

Matrix_Vron_t_T = double(subs(Matrix_Vron,t,T));

% vpa(Matrix_Vron_t_0,6)

% ------------------------------------------------------------------------%

% Определение неизвестных коэффициентов C

C_ = inv(Matrix_Vron_t_0) * X_0;

% ------------------------------------------------------------------------%

% Нахождение моментных функций

K_Tt_1 = subs (K_t,t, T - t);

K_Tt = diff (K_t);

K_Tt_2 = subs (K_Tt, t, T - t);

K_Ttt = diff (K_Tt);

K_Tt_3 = subs (K_Ttt, t, T - t);

K_Tttt = diff (K_Ttt);

K_Tt_4 = subs (K_Tttt, t, T - t);

K_Ttttt = diff (K_Tttt);

K_Tt_5 = subs (K_Ttttt, t, T - t);

h1_Tt = K_Tt_1

h2_Tt = K_Tt_2

h3_Tt = K_Tt_3

h4_Tt = K_Tt_4

h5_Tt = K_Tt_5

% ------------------------------------------------------------------------%

% Нахождение моментов

for i = 1 : poryadok

Matrix_a(i) = X_T(i) - C_' * Matrix_Vron_t_T(i,:)';

end

Matrix_a = Matrix_a'

% ------------------------------------------------------------------------%

RETURN = 2;

case '2'

disp('L - проблема моментов в пространстве состояний')

% ------------------------L - проблема моментов---------------------------%

% ----------------------в пространстве состояний--------------------------%

% ------------------------------------------------------------------------%

Matr_Ex_T = subs(MatrEx, t, T);

% ------------------------------------------------------------------------%

% Нахождение моментов

for i = 1 : poryadok

Matrix_a(i) = X_T(i) - Matr_Ex_T(i,:) * X_0;

end

Matrix_a = Matrix_a'

% ------------------------------------------------------------------------%

% Нахождение моментных функций

Matr_Ex_Tt = subs(MatrEx, t, T - t);

h_Tt = vpa(expand(simplify(Matr_Ex_Tt * B)),50);

h1_Tt = h_Tt(1)

h2_Tt = h_Tt(2)

h3_Tt = h_Tt(3)

h4_Tt = h_Tt(4)

h5_Tt = h_Tt(5)

% ------------------------------------------------------------------------%

RETURN = 2;

otherwise

disp('Неизвестный метод.')

RETURN = 1;

end

% h1_Tt = vpa(h1_Tt,6)

% h2_Tt = vpa(h2_Tt,6)

% h3_Tt = vpa(h3_Tt,6)

% h4_Tt = vpa(h4_Tt,6)

% h5_Tt = vpa(h5_Tt,6)

% ------------------------------------------------------------------------%

% --------Нахождение управления и вычисление минимальной энергии----------%

% ------------------------------------------------------------------------%

syms ks1 ks2 ks3 ks4 ks5

% ------------------------------------------------------------------------%

% Формирование функционала

d_v_2 = vpa (simplify (int ((ks1*h1_Tt + ks2*h2_Tt + ks3*h3_Tt + ...

ks4*h4_Tt + ks5*h5_Tt)^2, t, 0, T)), 50);

% Выражаем ks1 через остальные

ks1 = vpa ((1 - ks2*Matrix_a(2) - ks3*Matrix_a(3) - ...

ks4*Matrix_a(4) - ks5*Matrix_a(5))/Matrix_a(1), 50);

% Подставляем в функционал ks1

d_v_2 = vpa (expand (subs (d_v_2, ks1)), 50);

% Находим частные производные по ksi

eq_1= diff(d_v_2, ks2);

eq_2= diff(d_v_2, ks3);

eq_3= diff(d_v_2, ks4);

eq_4= diff(d_v_2, ks5);

% Решаем СЛАУ относительно ksi

ksi= solve(eq_1, eq_2, eq_3, eq_4);

% Полученные значения ksi

ks2= double(ksi.ks2)

ks3= double(ksi.ks3)

ks4= double(ksi.ks4)

ks5= double(ksi.ks5)

ks1 = double(vpa ((1 -ks2*Matrix_a(2) -ks3*Matrix_a(3) -ks4*Matrix_a(4) - ...

ks5*Matrix_a(5))/Matrix_a(1), 50))

% ------------------------------------------------------------------------%

% Проверка условия полученного результата

ks1*Matrix_a(1) + ks2*Matrix_a(2) + ks3*Matrix_a(3) + ...

ks4*Matrix_a(4) + ks5*Matrix_a(5)

% ------------------------------------------------------------------------%

% Вычисление управления и минимальной энергии

d_v_2 = vpa (simplify (int ((ks1*h1_Tt + ks2*h2_Tt + ks3*h3_Tt + ...

ks4*h4_Tt + ks5*h5_Tt)^2, t, 0, T)), 50)

% d_v_2 = double(d_v_2)

gamma_v_2 = 1/d_v_2

% gamma_v_2 = double(gamma_v_2)

u = vpa (expand(simplify(gamma_v_2 * (ks1*h1_Tt + ks2*h2_Tt + ks3*h3_Tt + ...

ks4*h4_Tt + ks5*h5_Tt))), 50)

% u = vpa(u,6)

u_0 = subs(u,t,0)

u_T = subs(u,t,T)

ezplot(u, [0 T], 1)

hl=legend('u(t)');

set(hl, 'FontName', 'Courier');

title ('u(t)');

xlabel('t')

grid on

% ------------------------------------------------------------------------%

% Нахождения X

% Вычисление матричной экспоненты

MatrEx = simplify (vpa(ilaplace(inv(s*eye(5) - A)), 50));

syms t tay

X_svob = MatrEx * X_0;

X_vinyg = int ((subs(MatrEx, t, t - tay))*B*(subs (u, t, tay)), tay, 0,t);

X_real = X_svob + X_vinyg;

save Sostoyaniya X_real u

X_real = vpa (expand (simplify(X_real)), 50)

X_real_0 = double(subs (X_real, t, 0))

X_real_T = double(subs (X_real, t, T))

% Погрешность X

delta_X_T = double(vpa(X_T - X_real_T, 50))

delta_X_0 = double(vpa(X_0 - X_real_0, 50))

% Нахождение Y

for i = 1 : poryadok - 1

Y_real(i) = B_(i,:) * X_real;

end

Y_real = vpa (expand(simplify(Y_real')), 50)

Y_real_0 = double(subs (Y_real, t, 0))

Y_real_T = double(subs (Y_real, t, T))

% Погрешность Y

delta_Y_T = double(vpa(Y_T - Y_real_T, 50))

delta_Y_0 = double(vpa(Y_0 - Y_real_0, 50))

% ------------------------------------------------------------------------%

% Вычисление max значений для задачи АКОР

h = 0.01;

tic

tt = 0 : h : T;

for i = 1 : poryadok

X_max(i) = max(abs(subs(X_real(i),t,tt)));

end

U_max = max(abs(subs(u,t,tt)));

toc

save Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Построение результатов X(t)

ezplot (X_real(1), [0 T],2)

title ('x_1(t)');

grid on

ezplot (X_real(2), [0 T],3)

title ('x_2(t)');

grid on

ezplot (X_real(3), [0 T],4)

title ('x_3(t)');

grid on

ezplot (X_real(4), [0 T],5)

title ('x_4(t)');

grid on

ezplot (X_real(5), [0 T],6)

title ('x_5(t)');

grid on

% Построение результатов Y(t)

ezplot (Y_real(1), [0 T],7)

title ('y_1(t)');

grid on

ezplot (Y_real(2), [0 T],8)

title ('y_2(t)');

grid on

ezplot (Y_real(3), [0 T],9)

title ('y_3(t)');

grid on

ezplot (Y_real(4), [0 T],10)

title ('y_4(t)');

grid on

% ------------------------------------------------------------------------%

Gramian_Uprav.m

clc

close all

clear all

format long

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Порядок системы

poryadok = 5;

% Начальные и конечные условия относительно вектора Y

Y_0 = [3 2 1 5]';

Y_T = [0 -1 0 3]';

% Конечное время перехода

T = 3;

% Матрица перехода от Н.У. Y к Н.У. X

B_ = [b0 b1 0 0 0;

0 b0 b1 0 0;

0 0 b0 b1 0;

0 0 0 b0 b1];

% ------------------------------------------------------------------------%

% Начальные условия для упорядоченной системы

X_0 = B_' * inv(B_ * B_') * Y_0

X_T = B_' * inv(B_ * B_') * Y_T

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4];

B = [0; 0; 0; 0; 1];

C = [b0 b1 0 0 0];

% ------------------------------------------------------------------------%

% Вычисление матричной экспоненты

syms s t

MatrEx = simplify (vpa(ilaplace(inv(s*eye(5) - A)), 50));

MatrEx_T = vpa(subs(MatrEx, t, T),50);

MatrEx_Tt = vpa(subs(MatrEx, t, T-t),50);

% ------------------------------------------------------------------------%

% Вычисление матрицы управляемости

M_c = [B A*B A^2*B A^3*B A^4*B]

rank_M_c = rank(M_c); %ранк = 5 - система управляема

% ------------------------------------------------------------------------%

% Вычисление грамиана управляемости

W_Tt = double(vpa(simplify(int(MatrEx_Tt*B*B'*MatrEx_Tt',t,0,T)),50))

% ------------------------------------------------------------------------%

% Формирование управления

u = vpa(expand(simplify(B'*MatrEx_Tt'*inv(W_Tt)*(X_T-MatrEx_T*X_0))),50)

u_0 = subs(u,t,0)

u_T = subs(u,t,T)

u = vpa(u,6)

% ------------------------------------------------------------------------%

ezplot(u, [0 T], 1)

title ('u(t)');

xlabel('t')

grid on

tt = 0 : 0.01 : T;

u2 = -20.605579750692850622177761310569*exp(-40.749492463732569440253455897187+13.583164154577523146751151965729*t)+19.011167813350479567880663060491*exp(-2.0544534472800777280645828326668+.68481781576002590935486094422228*t)+1.3356706538317879679656856470126*exp(-1.7550088311372150108106250409710+.58500294371240500360354168032368*t)*cos(-8.3032397968812277095785721047505+2.7677465989604092365261907015835*t)+7.2830359327562658520685140088852*exp(-1.7550088311372150108106250409710+.58500294371240500360354168032368*t)*sin(-8.3032397968812277095785721047505+2.7677465989604092365261907015835*t)-8.6096491449877801097840179781687;

u1 = subs(u2, t, tt);

u2 = subs(u, t, tt);

figure(2)

plot(tt,u1,'r',tt,u2,'b','LineWidth',2)

hl=legend('u(t) при решении оптимальной L-проблемы моментов','u(t) с использованием грамиана управляемости');

set(hl, 'FontName', 'Courier');

xlabel('t, cek'); ylabel('u(t)');

title('u(t)')

grid on

AKOR_stabilizaciya_na_polybeskon_interval.m

clc

clear all

close all

poryadok = 5;

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0;

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4]

B = [0; 0; 0; 0; 1]

C = [b0 b1 0 0 0]

% Начальные условия

X_0 = [10; 0; 6; 4; 8]

%T = 1;

Time = 1;

% ------------------------------------------------------------------------%

% Получение max значений из файла

load Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Нахождение элементов матриц Q и R

r(1) = 0.1;

q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;

for i = 2 : poryadok

q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;

end

Q = diag(q)

R = diag(r)

% Для изменения коэффициентов

% Q(1,1) = Q(1,1);

% Q(2,2) = Q(2,2);

% Q(3,3) = Q(3,3);

% Q(4,4) = Q(4,4);

% Q(5,5) = Q(5,5);

Q(1,1) = Q(1,1)*1e+12;

Q(2,2) = Q(2,2)*1e+8;

Q(3,3) = Q(3,3)*1e+7;

Q(4,4) = Q(4,4)*1e+0;

Q(5,5) = Q(5,5)*1e+2;

R(1,1) = R(1,1);

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом диагонализации

P1 = Solve_Riccati_Method_Diag(A,B,Q,R)

% ------------------------------------------------------------------------%

P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом обратного интегрирования

P2 = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach)

% ------------------------------------------------------------------------%

% Сравнение расхождения методов

Delta_P = abs(P1-P2)

% Построение графика коэффициентов регулятора

load Solve_Riccati_Method_Revers_Integr Time_R P N_str

PP = P;

for i = 1 : N_str

P = reshape(PP(i, :), poryadok, poryadok);

K(i, :) = -inv(R)*B'*P;

end

figure(2)

plot(Time_R,K(:,1),'-',Time_R,K(:,2),'-',Time_R,K(:,3),'-',Time_R,K(:,4),'-',Time_R,K(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты обратной связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

% Решение уравнения Риккати с помощью встроенной функции

% P = vpa(care(A,B,Q,R), 10)

% ------------------------------------------------------------------------%

% Нахождение коэффициентов регулятора

disp('Коэффициенты регулятора:')

K1 = -inv(R) * B' * P1

K2 = -inv(R) * B' * P2

% ------------------------------------------------------------------------%

A1_ = A + B * K1;

A2_ = A + B * K2;

% Вычисление матричной экспоненты

syms s t

MatrEx1 = simplify (vpa(ilaplace(inv(s*eye(5) - A1_)), 50));

MatrEx2 = simplify (vpa(ilaplace(inv(s*eye(5) - A2_)), 50));

% Нахождение координат состояния

X1 = vpa(simplify(MatrEx1 * X_0), 50);

X2 = vpa(simplify(MatrEx2 * X_0), 50);

% Нахождение управления

u1 = vpa(simplify(K1 * X1),50)

u2 = vpa(simplify(K2 * X2),50)

% ------------------------------------------------------------------------%

% Построение u(t) и X(t)

T_sravneniya = 0.2;

figure(3);

tt = 0 : 0.01 : T_sravneniya;

uu1 = subs(u1,t,tt);

uu2 = subs(u2,t,tt);

plot(tt, uu1, tt, uu2, 'LineWidth', 2)

title ('u(t)');

xlabel('t')

hl=legend('u(t) - управление',0);

set(hl,'FontName','Courier');

grid on

ezplot(X1(1), [0 Time], 4)

hold on

title ('x_1(t)');

xlabel('t')

grid on

ezplot(X1(2), [0 Time], 5)

title ('x_2(t)');

xlabel('t')

grid on

ezplot(X1(3), [0 Time], 6)

title ('x_3(t)');

xlabel('t')

grid on

ezplot(X1(4), [0 Time], 7)

title ('x_4(t)');

xlabel('t')

grid on

ezplot(X1(5), [0 Time], 8)

title ('x_5(t)');

xlabel('t')

grid on

tt = 0 : 0.01 : T_sravneniya;

X21 = subs(X1(1), t, tt);

X22= subs(X1(2), t, tt);

X23= subs(X1(3), t, tt);

X24= subs(X1(4), t, tt);

X25= subs(X1(5), t, tt);

save Sravnenie_stabilizacii_1 X21 X22 X23 X24 X25 uu1

AKOR_stabilizaciya_na_konech_interval.m

clc

clear all

close all

poryadok = 5;

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4];

B = [0; 0; 0; 0; 1];

C = [b0 b1 0 0 0];

% Начальные условия

X_0 = [10; 0; 6; 4; 8];

Time = 0.2;

% ------------------------------------------------------------------------%

% Получение max значений из файла

load Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Нахождение элементов матриц Q и R

% r(1) = 100;

r(1) = 0.1;

q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;

for i = 2 : poryadok

q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;

end

Q = diag(q);

R = diag(r);

% Для изменения коэффициентов

Q(1,1) = Q(1,1)*1e+12;

Q(2,2) = Q(2,2)*1e+8;

Q(3,3) = Q(3,3)*1e+7;

Q(4,4) = Q(4,4)*1e+0;

Q(5,5) = Q(5,5)*1e+2;

R(1,1) = R(1,1);

% P_prib = eye(poryadok, poryadok);

% P_prib(1,1) = 100;

% P_prib(2,2) = 10;

% % P_prib(3,3) = 1000;

% % P_prib(4,4) = 10;

% % P_prib(5,5) = 1;

% ------------------------------------------------------------------------%

P_nach = zeros(poryadok, poryadok);% + P_prib;

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом обратного интегрирования

P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach)

% ------------------------------------------------------------------------%

% Нахождение переменных коэффициентов регулятора

load Solve_Riccati_Method_Revers_Integr Time_R P N_str

PP = P;

for i = 1 : N_str

P = reshape(PP(i, :), poryadok, poryadok);

K(i, :) = -inv(R)*B'*P;

end

% ------------------------------------------------------------------------%

% Формирование вектора коэффициентов регулятора

% и решения уравнения Риккати в прямом порядке

load Solve_Riccati_Method_Revers_Integr P

size(K)

i = 1;

len_K = length(K(:,1))

for j = len_K : -1 : 1

K_pr(i,:) = K(j,:);

i = i + 1;

end

% ------------------------------------------------------------------------%

% Построение графика переменных коэффициентов регулятора в прямом времени

figure(2)

plot(Time_R,K(:,1),'-',Time_R,K(:,2),'-',Time_R,K(:,3),'-',...

Time_R,K(:,4),'-',Time_R,K(:,5),'-', 'LineWidth', 2);

grid on;

title('K(t)')

xlabel('t')

legend('k_1','k_2','k_3','k_4','k_5');

% ------------------------------------------------------------------------%

for k = 1 : len_K

A_(:,:,k) = A + B * K(k,:);

end

size(A_);

% ------------------------------------------------------------------------%

% Нахождение фазовых координат

X(:,1) = X_0;

h = 0.01;

time_X(1) = 0;

for k = 1 : len_K

X(:, k+1) = X(:, k) + h * A_(:,:,k) * X(:, k);

time_X(k+1) = time_X(k) + h;

end

X(:, k+1) = [];

time_X(k+1) = [];

% ------------------------------------------------------------------------%

% Нахождение управления

for k = 1 : len_K

u(k) = K_pr(k,:) * X(:,k);

end

% ------------------------------------------------------------------------%

% Построение u(t) и X(t)

figure(3);

plot(time_X, u, 'r-', 'LineWidth', 2)

title ('u(t)');

xlabel('t')

grid on

figure(4);

plot(time_X, X(1,:), 'LineWidth', 2)

hold on

title ('x_1(t)');

xlabel('t')

grid on

figure(5);

plot(time_X, X(2,:), 'LineWidth', 2)

title ('x_2(t)');

xlabel('t')

grid on

figure(6);

plot(time_X, X(3,:), 'LineWidth', 2)

title ('x_3(t)');

xlabel('t')

grid on

figure(7);

plot(time_X, X(4,:), 'LineWidth', 2)

title ('x_4(t)');

xlabel('t')

grid on

figure(8);

plot(time_X, X(5,:), 'LineWidth', 2)

title ('x_5(t)');

xlabel('t')

grid on

save Sravnenie_stabilizacii_2 time_X X u

Sravnenie_stabilizacii.m

close all

load Sravnenie_stabilizacii_1 X21 X22 X23 X24 X25 uu1

load Sravnenie_stabilizacii_2 time_X X u

figure(31);

plot(time_X, u, time_X, uu1, 'LineWidth', 2)

title ('u(t)');

xlabel('t')

hl=legend('u(t) - управление с перемен. коеф.','u(t) - управление с пост. коеф.');

set(hl,'FontName','Courier');

grid on

figure(41);

plot(time_X, X(1,:), time_X, X21, 'LineWidth', 2)

hold on

title ('x_1(t)');

xlabel('t')

hl=legend('x_1(t) - с перемен. коеф.','x_1(t) - с пост. коеф.');

set(hl,'FontName','Courier');

grid on

figure(51);

plot(time_X, X(2,:), time_X, X22,'LineWidth', 2)

title ('x_2(t)');

xlabel('t')

hl=legend('x_2(t) - с перемен. коеф.','x_2(t) - с пост. коеф.');

set(hl,'FontName','Courier');

grid on

figure(61);

plot(time_X, X(3,:), time_X, X23,'LineWidth', 2)

title ('x_3(t)');

xlabel('t')

hl=legend('x_3(t) - с перемен. коеф.','x_3(t) - с пост. коеф.');

set(hl,'FontName','Courier');

grid on

figure(71);

plot(time_X, X(4,:), time_X, X24,'LineWidth', 2)

title ('x_4(t)');

xlabel('t')

hl=legend('x_4(t) - с перемен. коеф.','x_4(t) - с пост. коеф.');

set(hl,'FontName','Courier');

grid on

figure(81);

plot(time_X, X(5,:), time_X, X25,'LineWidth', 2)

title ('x_5(t)');

xlabel('t')

hl=legend('x_5(t) - с перемен. коеф.','x_5(t) - с пост. коеф.');

set(hl,'FontName','Courier');

grid on

AKOR_stabilizaciya_pri_vozmusheniyah.m

clc

clear all

close all

warning off

poryadok = 5;

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4];

B = [0; 0; 0; 0; 1];

C = [b0 b1 0 0 0];

% Начальные условия

X_0 = [10; 0; 6; 4; 8];

Time = 1;

h = 0.01;

% ------------------------------------------------------------------------%

tic

% ------------------------------------------------------------------------%

% Получение max значений из файла

load Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Нахождение элементов матриц Q и R

r(1) = 100;

q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;

for i = 2 : poryadok

q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;

end

Q = diag(q);

R = diag(r);

% Для изменения коэффициентов

Q(1,1) = Q(1,1)*1e+12;

Q(2,2) = Q(2,2)*1e+8;

Q(3,3) = Q(3,3)*1e+7;

Q(4,4) = Q(4,4)*1e+0;

Q(5,5) = Q(5,5)*1e+2;

R(1,1) = R(1,1);

% P_0 = ones(poryadok, poryadok);

% P_0(1,1) = P_0(1,1)*1e12;

% P_0(2,2) = P_0(2,2)*1e8;

% P_0(3,3) = P_0(3,3)*1e7;

% P_0(4,4) = P_0(4,4)*1e0;

% P_0(5,5) = P_0(5,5)*1e2;

% ------------------------------------------------------------------------%

P_nach = zeros(poryadok, poryadok);%+P_0;

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом обратного интегрирования

P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach);

load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str

PP = P;

for k = 1 : N_str

P1 = reshape(PP(k, :), poryadok, poryadok);

for i = 1 : poryadok

for j = 1 : poryadok

P2(i,j,k) = P1(i,j);

end

size_P = size(P2);

% ------------------------------------------------------------------------%

tic

% ------------------------------------------------------------------------%

% Получение дискретных значений задающего воздействия в обратном времени

% для нахождения вспомогательной функции q(t)

Vozmyshyayushee_Vozdeistvie_Discrete_Revers(h, 0, Time);

% ------------------------------------------------------------------------%

load Vozmyshyayushee_Vozdeistvie_Discrete_Revers w_discrete_rev

% ------------------------------------------------------------------------%

size(w_discrete_rev);

% Начальное значение q(t)

q = zeros(poryadok,1);

% Интегрирование q(t) в обратном времени

for k = 1 : N_str

q(:, k+1) = q(:, k) - h * ((P2(:,:,k)*B*inv(R)*B'-A') * q(:, k) - P2(:,:,k)*w_discrete_rev(:,k));

end

q(:, k+1) = [];

size_q = size(q);

% ------------------------------------------------------------------------%

% Нахождение переменных коэффициентов регулятора

for k = 1 : N_str

K_o(k, :) = -inv(R) * B' * P2(:,:,k);

K_pr(k, :) = -inv(R) * B';

end

% Формирование вектора коэффициентов регулятора, значений задающего

% воздействия, значений вспомогательной функции в прямом порядке

size(K_o);

size(K_pr);

K_pr_p = K_pr;

i = 1;

len_K = length(K_o(:,1));

for j = len_K : -1 : 1

K_o_p(i,:) = K_o(j,:);

w_discrete(:,i) = w_discrete_rev(:,j);

q_pr(:, i) = q(:, j);

i = i + 1;

end

% ------------------------------------------------------------------------%

% Построение графика переменных коэффициентов регулятора обратной связи

% в прямом времени

toc

figure(3)

plot(Time_R,K_o(:,1),'-',Time_R,K_o(:,2),'-',Time_R,K_o(:,3),'-',...

Time_R,K_o(:,4),'-',Time_R,K_o(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты обратной связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

% Построение графика переменных коэффициентов регулятора прямой связи

% в прямом времени

figure(4)

plot(Time_R,K_pr(:,1),'-',Time_R,K_pr(:,2),'-',Time_R,K_pr(:,3),'-',...

Time_R,K_pr(:,4),'-',Time_R,K_pr(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты прямой связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_п_с','k_2_п_с','k_3_п_с','k_4_п_с','k_5_п_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

tic

% ------------------------------------------------------------------------%

for k = 1 : len_K

A_(:,:,k) = A + B * K_o_p(k,:);

end

size_A_ = size(A_);

% ------------------------------------------------------------------------%

% Нахождение фазовых координат

X(:,1) = X_0;

time_X(1) = 0;

for k = 1 : len_K

X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * q_pr(:,k) + w_discrete(:,k));

time_X(k+1) = time_X(k) + h;

end

X(:, k+1) = [];

time_X(k+1) = [];

size_X = size(X);

% ------------------------------------------------------------------------%

% Нахождение управления

for k = 1 : len_K

u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * q_pr(:,k);

end

size_u = size(u);

% ------------------------------------------------------------------------%

toc

% Построение u(t) и X(t)

figure(5);

plot(time_X, u, 'r-', 'LineWidth', 2)

title ('u(t)');

xlabel('t')

hl=legend('u(t) - управление',0);

set(hl,'FontName','Courier');

grid on

figure(6);

plot(time_X, X(1,:),'r-', time_X, w_discrete(1,:), 'LineWidth', 2)

hold on

title ('x_1(t)');

xlabel('t');

hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);

set(hl,'FontName','Courier');

grid on

figure(7);

plot(time_X, X(2,:),'r-', time_X, w_discrete(2,:), 'LineWidth', 2)

title ('x_2(t)');

xlabel('t');

hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);

set(hl,'FontName','Courier');

grid on

figure(8);

plot(time_X, X(3,:),'r-', time_X, w_discrete(3,:), 'LineWidth', 2)

title ('x_3(t)');

xlabel('t');

hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);

set(hl,'FontName','Courier');

grid on

figure(9);

plot(time_X, X(4,:),'r-', time_X, w_discrete(4,:), 'LineWidth', 2)

title ('x_4(t)');

xlabel('t');

hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);

set(hl,'FontName','Courier');

grid on

figure(10);

plot(time_X, X(5,:),'r-', time_X, w_discrete(5,:), 'LineWidth', 2)

title ('x_5(t)');

xlabel('t');

hl=legend('X(t) - реальный сигнал','w(t) - возмущающее воздействие',0);

set(hl,'FontName','Courier');

grid on

figure(11);

plot(time_X, q(1,:), time_X, q(2,:), time_X, q(3,:), time_X, q(4,:), time_X, q(5,:), 'LineWidth', 2)

title ('q(t)- vector-function');

xlabel('t');

hl=legend('q_1(t)', 'q_2(t)', 'q_3(t)', 'q_4(t)', 'q_5(t)');

set(hl,'FontName','Courier');

grid on

AKOR_slegenie_na_konech_interval_I_podxod.m

clc

clear all

close all

poryadok = 5;

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4];

B = [0; 0; 0; 0; 1];

C = [b0 b1 0 0 0];

% Начальные условия

X_0 = [10; 0; 6; 4; 8;];

Time = 1;

% ------------------------------------------------------------------------%

% Получение max значений из файла

load Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Нахождение элементов матриц Q и R

r(1) = 100;

q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;

for i = 2 : poryadok

q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;

end

Q = diag(q);

R = diag(r);

% Для изменения коэффициентов

% Q(1,1) = Q(1,1)*1e+10;

% Q(2,2) = Q(2,2)*1e+8;

% Q(3,3) = Q(3,3)*1e+6;

% Q(4,4) = Q(4,4)*1e+2;

% Q(5,5) = Q(5,5)*1e+2;

Q(1,1) = Q(1,1)*1e+12;

Q(2,2) = Q(2,2)*1e+8;

Q(3,3) = Q(3,3)*1e+7;

Q(4,4) = Q(4,4)*1e+0;

Q(5,5) = Q(5,5)*1e+2;

R(1,1) = R(1,1);

% ------------------------------------------------------------------------%

% Задающее воздействие

A_o = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4];

X_o_0 = [12; 10; 14; 8; 16];

% ------------------------------------------------------------------------%

% Расширенный вектор состояния и расширенные матрицы A,B,Q

%X_rassh = [X_0; X_o];

NULL_M1 = zeros(size(A));

A_rassh = [A NULL_M1;

NULL_M1 A_o];

NULL_M2 = zeros(length(A(:,1)), 1);

B_rassh = [B; NULL_M2];

Q_rassh = [Q -Q;

-Q Q];

X_rassh_0 = [X_0; X_o_0]

% ------------------------------------------------------------------------%

P_nach = zeros(2*poryadok, 2*poryadok);%+ones(poryadok, poryadok);

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом обратного интегрирования

P = Solve_Riccati_Method_Revers_Integr(A_rassh,B_rassh,Q_rassh,R,Time,2*poryadok, P_nach)

% ------------------------------------------------------------------------%

% Нахождение переменных коэффициентов регулятора

load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str

% ------------------------------------------------------------------------%

% % Формирование матриц P11 и P12

PP = P;

for k = 1 : N_str

P = reshape(PP(k, :), 2*poryadok, 2*poryadok);

for i = 1 : poryadok

for j = 1 : poryadok

P11(i,j,k) = P(i,j);

end

for i = 1 : poryadok

for j = (poryadok+1) : (2*poryadok)

P12(i,j-poryadok,k) = P(i,j);

end

P11(:,:,k)

P12(:,:,k)

% ------------------------------------------------------------------------%

for k = 1 : N_str

K_o(k, :) = -inv(R) * B' * P11(:,:,k);

K_pr(k, :) = -inv(R) * B' * P12(:,:,k);

end

% Формирование вектора коэффициентов регулятора

% в прямом порядке

size(K_o)

size(K_pr)

i = 1;

len_K = length(K_o(:,1))

for j = len_K : -1 : 1

K_o_p(i,:) = K_o(j,:)

K_pr_p(i,:) = K_pr(j,:);

i = i + 1;

end

% ------------------------------------------------------------------------%

% Построение графика переменных коэффициентов регулятора обратной связи

% в прямом времени

figure(2)

plot(Time_R,K_o(:,1),'-',Time_R,K_o(:,2),'-',Time_R,K_o(:,3),'-',...

Time_R,K_o(:,4),'-',Time_R,K_o(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты обратной связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

% Построение графика переменных коэффициентов регулятора прямой связи

% в прямом времени

figure(3)

plot(Time_R,K_pr(:,1),'-',Time_R,K_pr(:,2),'-',Time_R,K_pr(:,3),'-',...

Time_R,K_pr(:,4),'-',Time_R,K_pr(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты прямой связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_п_с','k_2_п_с','k_3_п_с','k_4_п_с','k_5_п_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

% Нахождение отслеживаемого сигнала

X_o(:,1) = X_o_0;

h = 0.01;

for k = 1 : len_K

X_o(:, k+1) = X_o(:, k) + h * A_o * X_o(:, k);

end

X_o(:, k+1) = [];

% ------------------------------------------------------------------------%

for k = 1 : len_K

A_(:,:,k) = A + B * K_o_p(k,:);

end

size(A_)

% ------------------------------------------------------------------------%

% Нахождение фазовых координат

X(:,1) = X_0;

time_X(1) = 0;

for k = 1 : len_K

X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * X_o(:,k));

time_X(k+1) = time_X(k) + h;

end

X(:, k+1) = [];

time_X(k+1) = [];

% ------------------------------------------------------------------------%

% Нахождение управления

for k = 1 : len_K

u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * X_o(:,k);

end

% ------------------------------------------------------------------------%

% Построение u(t) и X(t)

figure(4);

plot(time_X, u, 'r-', 'LineWidth', 2)

title ('u(t)');

xlabel('t')

hl=legend('u(t) - управление',0);

set(hl,'FontName','Courier');

grid on

figure(5);

plot(time_X, X(1,:),'r-', time_X, X_o(1,:), 'LineWidth', 2)

hold on

title ('x_1(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(6);

plot(time_X, X(2,:),'r-', time_X, X_o(2,:), 'LineWidth', 2)

title ('x_2(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(7);

plot(time_X, X(3,:),'r-', time_X, X_o(3,:), 'LineWidth', 2)

title ('x_3(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(8);

plot(time_X, X(4,:),'r-', time_X, X_o(4,:), 'LineWidth', 2)

title ('x_4(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(9);

plot(time_X, X(5,:),'r-', time_X, X_o(5,:), 'LineWidth', 2)

title ('x_5(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

AKOR_slegenie_na_konech_interval_II_podxod.m

clc

clear all

close all

poryadok = 5;

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4];

B = [0; 0; 0; 0; 1];

C = [b0 b1 0 0 0];

% Начальные условия

X_0 = [10; 0; 6; 4; 8];

Time = 45;

h = 0.01;

H = 0.8;

% ------------------------------------------------------------------------%

tic

% ------------------------------------------------------------------------%

% Получение max значений из файла

load Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Нахождение элементов матриц Q и R

r(1) = 100;

q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;

for i = 2 : poryadok

q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;

end

Q = diag(q);

R = diag(r);

% Для изменения коэффициентов

% Q(1,1) = Q(1,1)*1e+12;

% Q(2,2) = Q(2,2)*1e+8;

% Q(3,3) = Q(3,3)*1e+7;

% Q(4,4) = Q(4,4)*1e+0;

% Q(5,5) = Q(5,5)*1e+2;

R(1,1) = R(1,1);

% ------------------------------------------------------------------------%

P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом обратного интегрирования

P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach);

load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str

PP = P;

for k = 1 : N_str

P1 = reshape(PP(k, :), poryadok, poryadok);

for i = 1 : poryadok

for j = 1 : poryadok

P2(i,j,k) = P1(i,j);

end

size_P = size(P2)

% ------------------------------------------------------------------------%

tic

% ------------------------------------------------------------------------%

% Получение дискретных значений задающего воздействия в обратном времени

% для нахождения вспомогательной функции q(t)

Zadayushee_Vozdeistvie_Discrete_Revers_Modern(h, 0, Time);

% ------------------------------------------------------------------------%

load Zadayushee_Vozdeistvie_Discrete_Revers X_o_discrete_rev

% ------------------------------------------------------------------------%

size(X_o_discrete_rev);

% Нахождение q(t)

for i = 1 : poryadok

qq = -P_nach(:,:,1) * X_o_discrete_rev(i,1);

q(i,1) = qq(i,1);

end

% Интегрирование q(t) в обратном времени

for k = 1 : N_str

q(:, k+1) = q(:, k) - h * ((P2(:,:,k)*B*inv(R)*B'-A') * q(:, k) + Q*X_o_discrete_rev(:,k));

end

q(:, k+1) = [];

size_q = size(q)

% ------------------------------------------------------------------------%

% Нахождение переменных коэффициентов регулятора

for k = 1 : N_str

K_o(k, :) = -inv(R) * B' * P2(:,:,k);

K_pr(k, :) = -inv(R) * B';

end

% Формирование вектора коэффициентов регулятора, значений задающего

% воздействия, значений вспомогательной функции в прямом порядке

size(K_o);

size(K_pr);

K_pr_p = K_pr;

i = 1;

len_K = length(K_o(:,1));

for j = len_K : -1 : 1

K_o_p(i,:) = K_o(j,:);

X_o_discrete(:,i) = X_o_discrete_rev(:,j);

q_pr(:, i) = q(:, j);

i = i + 1;

end

% ------------------------------------------------------------------------%

% Построение графика переменных коэффициентов регулятора обратной связи

% в прямом времени

toc

figure(3)

plot(Time_R,K_o(:,1),'-',Time_R,K_o(:,2),'-',Time_R,K_o(:,3),'-',...

Time_R,K_o(:,4),'-',Time_R,K_o(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты обратной связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

% Построение графика переменных коэффициентов регулятора прямой связи

% в прямом времени

figure(4)

plot(Time_R,K_pr(:,1),'-',Time_R,K_pr(:,2),'-',Time_R,K_pr(:,3),'-',...

Time_R,K_pr(:,4),'-',Time_R,K_pr(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты прямой связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_п_с','k_2_п_с','k_3_п_с','k_4_п_с','k_5_п_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

tic

% ------------------------------------------------------------------------%

for k = 1 : len_K

A_(:,:,k) = A + B * K_o_p(k,:);

end

size_A_ = size(A_)

% ------------------------------------------------------------------------%

% Нахождение фазовых координат

X(:,1) = X_0;

time_X(1) = 0;

for k = 1 : len_K

X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * q_pr(:,k));

time_X(k+1) = time_X(k) + h;

end

X(:, k+1) = [];

time_X(k+1) = [];

size_X = size(X)

% ------------------------------------------------------------------------%

% Нахождение управления

for k = 1 : len_K

u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * q_pr(:,k);

end

size_u = size(u)

% ------------------------------------------------------------------------%

toc

% Построение u(t) и X(t)

figure(5);

plot(time_X, u, 'r-', 'LineWidth', 2)

title ('u(t)');

xlabel('t')

hl=legend('u(t) - управление',0);

set(hl,'FontName','Courier');

grid on

figure(6);

plot(time_X, X(1,:),'r-', time_X, X_o_discrete(1,:), time_X, X_o_discrete(1,:)-0.8,'LineWidth', 2)

hold on

title ('x_1(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон', 'уровень',0);

set(hl,'FontName','Courier');

grid on

figure(7);

plot(time_X, X(2,:),'r-', time_X, X_o_discrete(2,:), 'LineWidth', 2)

title ('x_2(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(8);

plot(time_X, X(3,:),'r-', time_X, X_o_discrete(3,:), 'LineWidth', 2)

title ('x_3(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(9);

plot(time_X, X(4,:),'r-', time_X, X_o_discrete(4,:), 'LineWidth', 2)

title ('x_4(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(10);

plot(time_X, X(5,:),'r-', time_X, X_o_discrete(5,:), 'LineWidth', 2)

title ('x_5(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

AKOR_slegenie_so_skolz_intervalami_Modern.m

function AKOR_slegenie_so_skolz_intervalami_Modern

clc

clear all

close all

poryadok = 5;

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4];

B = [0; 0; 0; 0; 1];

C = [b0 b1 0 0 0];

% Начальные условия

X_0 = [10; 0; 6; 4; 8];

Time = 45;

Kolvo_intervalov = 3;

h = 0.01;

H = 0.8;

% ------------------------------------------------------------------------%

% Получение max значений из файла

load Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Нахождение элементов матриц Q и R

r(1) = 100;

q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;

for i = 2 : poryadok

q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;

end

Q = diag(q);

R = diag(r);

% Для изменения коэффициентов

% Q(1,1) = Q(1,1)*1e+13;

% Q(2,2) = Q(2,2)*1e+10;

% Q(3,3) = Q(3,3)*1e+8;

% Q(4,4) = Q(4,4)*1e+5;

% Q(5,5) = Q(5,5)*1e+2;

R(1,1) = R(1,1);

% ------------------------------------------------------------------------%

% ------------------Скользящие интервалы----------------------------------%

shag = Time/Kolvo_intervalov;

Time1 = shag

Time2 = 2*shag

Time3 = Time

% ------------------------------------------------------------------------%

P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом обратного интегрирования

P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time1,poryadok, P_nach);

load Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str

PP = P;

for k = 1 : N_str

P1 = reshape(PP(k, :), poryadok, poryadok);

for i = 1 : poryadok

for j = 1 : poryadok

P2(i,j,k) = P1(i,j);

end

size_P = size(P2)

% ------------------------------------------------------------------------%

% Нахождение переменных коэффициентов регулятора

for k = 1 : N_str

K_o(k, :) = -inv(R) * B' * P2(:,:,k);

K_pr(k, :) = -inv(R) * B';

end

% ------------------------------------------------------------------------%

tic

% 1 интервал

Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, 0, Time1, X_0, poryadok, K_o, K_pr);

load Solve_Interval time_X X u X_o_discrete

time_X1 = time_X;

X1 = X;

u1 = u;

X_o_discrete1 = X_o_discrete;

% 2 интервал

Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, Time1, Time2, X1(:,N_str), poryadok, K_o, K_pr);

load Solve_Interval time_X X u X_o_discrete

time_X2 = time_X;

X2 = X;

u2 = u;

X_o_discrete2 = X_o_discrete;

% 3 интервал

Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, Time2, Time3, X2(:,N_str), poryadok, K_o, K_pr);

load Solve_Interval time_X X u X_o_discrete

time_X3 = time_X;

X3 = X;

u3 = u;

X_o_discrete3 = X_o_discrete;

toc

% ------------------------------------------------------------------------%

% Объединение интервалов

time_X = [time_X1 time_X2 time_X3];

u = [u1 u2 u3];

X = [X1 X2 X3];

X_o_discrete = [X_o_discrete1 X_o_discrete2 X_o_discrete3];

% ------------------------------------------------------------------------%

% Построение u(t) и X(t)

figure(3);

plot(time_X, u, 'r-','LineWidth', 2);

title ('u(t)');

xlabel('t')

hl=legend('u(t) - управление',0);

set(hl,'FontName','Courier');

grid on

figure(4);

plot(time_X, X(1,:),'r-', time_X, X_o_discrete(1,:), time_X, X_o_discrete(1,:)-0.8,'LineWidth', 2)

hold on

title ('x_1(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон', 'уровень',0);

set(hl,'FontName','Courier');

grid on

figure(5);

plot(time_X, X(2,:),'r-', time_X, X_o_discrete(2,:), 'LineWidth', 2)

title ('x_2(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(6);

plot(time_X, X(3,:),'r-', time_X, X_o_discrete(3,:), 'LineWidth', 2)

title ('x_3(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(7);

plot(time_X, X(4,:),'r-', time_X, X_o_discrete(4,:), 'LineWidth', 2)

title ('x_4(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

figure(8);

plot(time_X, X(5,:),'r-', time_X, X_o_discrete(5,:), 'LineWidth', 2)

title ('x_5(t)');

xlabel('t');

hl=legend('X(t) - слежение','X_o(t) - эталон',0);

set(hl,'FontName','Courier');

grid on

function Solve_Interval(P_nach, N_str, h, P2, A,B,Q,R, T_nach, T_konech, X_0, poryadok, K_o, K_pr)

Zadayushee_Vozdeistvie_Discrete_Revers_Modern(h, T_nach, T_konech);

load Zadayushee_Vozdeistvie_Discrete_Revers X_o_discrete_rev

% ------------------------------------------------------------------------%

% Нахождение q(t)

for i = 1 : poryadok

qq = -P_nach(:,:,1) * X_o_discrete_rev(i,1);

q(i,1) = qq(i,1);

end

% Интегрирование q(t) в обратном времени

for k = 1 : N_str

q(:, k+1) = q(:, k) - h * ((P2(:,:,k)*B*inv(R)*B'-A') * q(:, k) + Q*X_o_discrete_rev(:,k));

end

q(:, k+1) = [];

size_q = size(q)

% ------------------------------------------------------------------------%

% Формирование вектора коэффициентов регулятора, значений задающего

% воздействия, значений вспомогательной функции в прямом порядке

K_pr_p = K_pr;

i = 1;

for j = N_str : -1 : 1

K_o_p(i,:) = K_o(j,:);

X_o_discrete(:,i) = X_o_discrete_rev(:,j);

q_pr(:, i) = q(:, j);

i = i + 1;

end

% ------------------------------------------------------------------------%

for k = 1 : N_str

A_(:,:,k) = A + B * K_o_p(k,:);

end

size_A_ = size(A_)

% ------------------------------------------------------------------------%

% Нахождение фазовых координат

X(:,1) = X_0;

time_X(1) = T_nach;

for k = 1 : N_str

X(:, k+1) = X(:, k) + h * (A_(:,:,k) * X(:, k) + B * K_pr_p(k,:) * q_pr(:,k));

time_X(k+1) = time_X(k) + h;

end

X(:, k+1) = [];

time_X(k+1) = [];

size_X = size(X)

% ------------------------------------------------------------------------%

% Нахождение управления

for k = 1 : N_str

u(k) = K_o_p(k,:) * X(:,k) + K_pr_p(k,:) * q_pr(:,k);

end

size_u = size(u)

save Solve_Interval time_X X u X_o_discrete

Sintez_nablyud_polnogo_poryadka.m

clc

clear all

close all

poryadok = 5;

% ------------------------------------------------------------------------%

b_0 = 5;

b_1 = 9;

% Укороченная система данного объекта

a_5 = 0.1153;

a_4 = 1.78;

a_3 = 3.92;

a_2 = 14.42;

a_1 = 8.583;

a_0 = 0;

% ------------------------------------------------------------------------%

% Приведение системы

b0 = b_0/a_5;

b1 = b_1/a_5;

a5 = a_5/a_5;

a4 = a_4/a_5;

a3 = a_3/a_5;

a2 = a_2/a_5;

a1 = a_1/a_5;

a0 = a_0/a_5;

% ------------------------------------------------------------------------%

% Представление системы в пространстве состояний

A = [0 1 0 0 0;

0 0 1 0 0;

0 0 0 1 0;

0 0 0 0 1;

-a0 -a1 -a2 -a3 -a4]

B = [0; 0; 0; 0; 1]

C = [b0 b1 0 0 0]

% Начальные условия

X_0 = [10; 0; 6; 4; 8]

Time = 10;

% ------------------------------------------------------------------------%

% Получение max значений из файла

load Sostoyaniya X_max U_max

% ------------------------------------------------------------------------%

% Нахождение элементов матриц Q и R

r(1) = 100;

q(1) = 1/poryadok * r(1) * (U_max)^2 / (X_max(1))^2;

for i = 2 : poryadok

q(i) = q(1) * (X_max(1))^2 / (X_max(i))^2;

end

Q = diag(q)

R = diag(r)

% Для изменения коэффициентов

Q(1,1) = Q(1,1);

Q(2,2) = Q(2,2);

Q(3,3) = Q(3,3);

Q(4,4) = Q(4,4);

Q(5,5) = Q(5,5);

% Q(1,1) = Q(1,1)*1e+12;

% Q(2,2) = Q(2,2)*1e+8;

% Q(3,3) = Q(3,3)*1e+7;

% Q(4,4) = Q(4,4)*1e+0;

% Q(5,5) = Q(5,5)*1e+2;

R(1,1) = R(1,1);

% ------------------------------------------------------------------------%

P_nach = zeros(poryadok, poryadok);%+ones(poryadok, poryadok);

% ------------------------------------------------------------------------%

% Решение уравнения Риккати методом обратного интегрирования

P1 = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P_nach)

% ------------------------------------------------------------------------%

% Построение графика коэффициентов регулятора

load Solve_Riccati_Method_Revers_Integr Time_R P N_str

PP = P;

for i = 1 : N_str

P = reshape(PP(i, :), poryadok, poryadok);

K(i, :) = -inv(R)*B'*P;

end

figure(2)

plot(Time_R,K(:,1),'-',Time_R,K(:,2),'-',Time_R,K(:,3),'-',Time_R,K(:,4),'-',Time_R,K(:,5),'-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Коэффициенты обратной связи в прямом времени');

set(tit1,'FontName','Courier');

hl=legend('k_1_о_с','k_2_о_с','k_3_о_с','k_4_о_с','k_5_о_с',0);

set(hl,'FontName','Courier');

grid on;

% ------------------------------------------------------------------------%

% Нахождение коэффициентов регулятора

disp('Коэффициенты регулятора:')

K = -inv(R) * B' * P1

% ------------------------------------------------------------------------%

A_ = A + B * K;

% ------------------------------------------------------------------------%

% Нахождение фазовых координат

X(:,1) = X_0;

h = 0.01;

time_X(1) = 0;

for k = 1 : N_str

X(:, k+1) = X(:, k) + h * A_ * X(:, k);

time_X(k+1) = time_X(k) + h;

end

X(:, k+1) = [];

time_X(k+1) = [];

% ------------------------------------------------------------------------%

% Нахождение управления

for k = 1 : N_str

u(k) = K * X(:,k);

end

% ------------------------------------------------------------------------%

% Нахождение коэффициентов наблюдателя

M_n = [C' A'*C' (A^2)'*C' (A^3)'*C' (A^4)'*C']

rank_M_n = rank(M_n)

A_r = A_

disp('Спектр матрицы регулятора:')

spektr_A_r = eig(A_r)

koeff = 1;

min_lyamda_A_r = min(real(spektr_A_r))

% lyamda = min_lyamda_A_r * koeff;

lyamda = -5;

disp('Спектр матрицы наблюдателя эталонный:')

lyamda_A_n = [lyamda - koeff * 4; lyamda - koeff * 3; lyamda - koeff * 2;...

lyamda - koeff; lyamda]'

syms k_n1 k_n2 k_n3 k_n4 k_n5 lyam

K_n = [k_n1; k_n2; k_n3; k_n4; k_n5];

Koeff_poly_n_etalon = poly(lyamda_A_n)

disp('Характеристический полином наблюдателя эталонный:')

poly_n_etalon = poly2sym(Koeff_poly_n_etalon, lyam)

disp('Характеристический полином наблюдателя реальный:')

poly_n_real = collect(expand(simplify(det(lyam*eye(poryadok) - (A - K_n*C)))),lyam)

raznost_poly = collect(poly_n_etalon-poly_n_real,lyam)

for i = 1 : poryadok

Koeff_raznost_poly(i) = subs(diff(raznost_poly,poryadok-i,lyam)/factorial(poryadok-i),lyam,0);

end

Koeff_raznost_poly

[Kn1 Kn2 Kn3 Kn4 Kn5]= solve(Koeff_raznost_poly(5), Koeff_raznost_poly(4),...

Koeff_raznost_poly(3), Koeff_raznost_poly(2), Koeff_raznost_poly(1), ...

k_n1, k_n2, k_n3, k_n4, k_n5)

Kn = [Kn1; Kn2; Kn3; Kn4; Kn5];

Kn = vpa(Kn,50)

% Проверка

Proverka = solve(det(lyam*eye(poryadok)-(A-Kn*C)))

% ------------------------------------------------------------------------%

% Нахождение x и x_оценочного

X_ocen_0 = [0 0 0 0 0]';

A_rash = [A B*K;

Kn*C A-Kn*C+B*K]

X_rash_0 = [X_0;X_ocen_0]

X_rash(:,1) = X_rash_0;

for k = 1 : N_str

X_rash(:,k+1) = X_rash(:,k) + h * A_rash * X_rash(:,k);

end

X_rash(:,k+1) = [];

% ------------------------------------------------------------------------%

% Разделение x и x_оценочного

for i = 1 : poryadok

X_n(i,:) = X_rash(i,:);

end

for i = poryadok + 1 : 2*poryadok

X_n_ocen(i - poryadok,:) = X_rash(i,:);

end

% ------------------------------------------------------------------------%

% Нахождение управления

for i = 1 : N_str

u_n(i) = K * X_n_ocen(:,i);

end

% Построение u(t) и X(t)

figure(3);

plot(time_X, u, 'r-', time_X, u_n, 'b-', 'LineWidth', 2)

title ('u(t)');

xlabel('t')

hl=legend('управление без наблюдателя','управление c наблюдателем');

set(hl,'FontName','Courier');

grid on

figure(4);

plot(time_X, X(1,:), time_X, X_n(1,:), time_X, X_n_ocen(1,:),'LineWidth', 2)

hold on

title ('x_1(t)');

xlabel('t')

hl=legend('x_1(t) без наблюдателя','x_1(t) c наблюдателем', 'x_о_ц_е_н_1(t)');

set(hl,'FontName','Courier');

grid on

figure(5);

plot(time_X, X(2,:), time_X, X_n(2,:), time_X, X_n_ocen(2,:),'LineWidth', 2)

title ('x_2(t)');

xlabel('t')

hl=legend('x_2(t) без наблюдателя','x_2(t) c наблюдателем', 'x_о_ц_е_н_2(t)');

set(hl,'FontName','Courier');

grid on

figure(6);

plot(time_X, X(3,:), time_X, X_n(3,:), time_X, X_n_ocen(3,:),'LineWidth', 2)

title ('x_3(t)');

xlabel('t')

hl=legend('x_3(t) без наблюдателя','x_3(t) c наблюдателем', 'x_о_ц_е_н_3(t)');

set(hl,'FontName','Courier');

grid on

figure(7);

plot(time_X, X(4,:), time_X, X_n(4,:), time_X, X_n_ocen(4,:),'LineWidth', 2)

title ('x_4(t)');

xlabel('t')

hl=legend('x_4(t) без наблюдателя','x_4(t) c наблюдателем', 'x_о_ц_е_н_4(t)');

set(hl,'FontName','Courier');

grid on

figure(8);

plot(time_X, X(5,:), time_X, X_n(5,:), time_X, X_n_ocen(5,:),'LineWidth', 2)

title ('x_5(t)');

xlabel('t')

hl=legend('x_5(t) без наблюдателя','x_5(t) c наблюдателем', 'x_о_ц_е_н_5(t)');

set(hl,'FontName','Courier');

grid on

Solve_Riccati_Method_Diag.m

% ------------------------------------------------------------------------%

% Метод диагонализации для решения алгебраического уравнения Риккати

function P = Solve_Riccati_Method_Diag(A,B,Q,R)

% Расширенная матрица системы

Z = [A B*inv(R)*B';

Q -A']

% Нахождение собственных векторов и собственных чисел матрицы Z

[V,D] = eig(Z)

% ------------------------------------------------------------------------%

% Построение матрицы S

% Индексы столбцов собственных значений Re(lyamda) > 0

Ind_Re_plus = find(sum(real(D)) > 0);

% Индексы столбцов собственных значений Re(lyamda) < 0

Ind_Re_minus = find(sum(real(D)) < 0);

% Формирование матрицы D в виде Re(lyamda) > 0 -> Re(lyamda) < 0

D1 = sum(D(:, Ind_Re_plus));

D2 = sum(D(:, Ind_Re_minus));

D = [D1 D2];

% Формирование матрицы S в виде Re(lyamda) > 0 -> Re(lyamda) < 0

S1 = V(:, Ind_Re_plus);

S2 = V(:, Ind_Re_minus);

S = [S1 S2];

% Поиск столбцов с комплексными корнями в матрице D

Ind_Complex_D = find(imag(D) ~= 0);

% Формирование конечной матрицы S

for i = 1 : 2 : length(Ind_Complex_D)

S (:, Ind_Complex_D(i) + 1) = imag(S(:, Ind_Complex_D(i)));

S (:, Ind_Complex_D(i)) = real(S(:, Ind_Complex_D(i)));

end

S = S

% ------------------------------------------------------------------------%

poryadok = length(A(1,:));

S12 = S(1 : poryadok, poryadok+1 : 2*poryadok);

S22 = S(poryadok+1 : 2*poryadok, poryadok+1 : 2*poryadok);

% ------------------------------------------------------------------------%

% Вычисление матрицы P

P = -S22 * inv(S12);

Solve_Riccati_Method_Revers_Integr.m

% ------------------------------------------------------------------------%

% Решение уравнения Риккати интегрированием в обратном времени

function P = Solve_Riccati_Method_Revers_Integr(A,B,Q,R,Time,poryadok, P1)

save For_Riccati A B Q R poryadok

% Решение дифференциального уравнения Риккати

P1 = reshape(P1, poryadok^2, 1);

[Time_R, P] = ode45(@Riccati, [Time : -0.01 : 0], P1);

[N_str, N_stolb] = size(P);

% Построение полученного решения

figure(1)

for i = 1 : poryadok^2

plot(Time_R, P(:,i),'-')

hold on

end

% plot(Time_R,P(:,1),'-',Time_R,P(:,2),'-',Time_R,P(:,3),'-',Time_R,P(:,4),'-',Time_R,P(:,5),'-',Time_R,P(:,6),'-',...

% Time_R,P(:,7),'-',Time_R,P(:,8),'-',Time_R,P(:,9),'-',Time_R,P(:,10),'-',Time_R,P(:,11),'-',Time_R,P(:,12),'-',...

% Time_R,P(:,13),'-',Time_R,P(:,14),'-',Time_R,P(:,15),'-',Time_R,P(:,16),'-',Time_R,P(:,17),'-',Time_R,P(:,18),'-',...

% Time_R,P(:,19),'-',Time_R,P(:,20),'-',Time_R,P(:,21),'-',Time_R,P(:,22),'-',Time_R,P(:,23),'-',Time_R,P(:,24),'-',...

% Time_R,P(:,25),'-', 'lineWidth', 2);

grid on;

tit1 = title('Решения уравнения Риккати');

set(tit1,'FontName','Courier');

xlabel('t');

% legend('p_1','p_2','p_3','p_4','p_5','p_6','p_7','p_8','p_9','p_1_0','p_1_1','p_1_2','p_1_3','p_1_4','p_1_5','p_1_6',...

% 'p_1_7','p_1_8','p_1_9','p_2_0','p_2_1','p_2_2','p_2_3','p_2_4','p_2_5');

save Solve_Riccati_Method_Revers_Integr Time_R P N_str

save Solve_Riccati_Method_Revers_Integr_for_slegenie Time_R P N_str

P = reshape(P(N_str,:), poryadok, poryadok);

function dP = Riccati(Time,P)

load For_Riccati A B Q R poryadok

P = reshape(P, poryadok, poryadok);

% Дифференциальное уравнение Риккати

dP = -P*A - A'*P + P*B*inv(R)*B'*P - Q;

dP = reshape(dP, poryadok^2, 1);

Vozmyshyayushee_Vozdeistvie_Discrete_Revers.m

% Получение дискретных значений возмущающего воздействия в обратном времени

% для нахождения вспомогательной функции q(t)

function Vozmyshyayushee_Vozdeistvie_Discrete_Revers(h, T_nach, T_konech)

% ------------------------------------------------------------------------%

% Возмущающее воздействие

A = 1;

w = 4*pi;

k = 1;

RETURN = 1;

while RETURN == 1

disp('Возмущающее воздействие - const: 1')

disp('Возмущающее воздействие - A*sin(w*t): 2')

reply = input('Выберете возмущающее воздействие [1 или 2]: ', 's');

switch reply

case '1'

disp('Возмущающее воздействие - const')

for t = T_konech: -h : T_nach

w_discrete_rev(:, k) = [A + 0 * t; 0; 0; 0; 0];

k = k + 1;

end

RETURN = 2;

case '2'

disp('Возмущающее воздействие - A*sin(w*t)')

for t = T_konech: -h : T_nach

w_discrete_rev(:, k) = [A * sin(w * t); 0; 0; 0; 0];

k = k + 1;

end

RETURN = 2;

otherwise

disp('Неизвестное воздействие.')

RETURN = 1;

end

figure(2)

t = T_konech : -h : T_nach;

plot(t, w_discrete_rev(1,:), 'r-', 'LineWidth', 2);

xlabel('t')

tit1 = title('Возмущающее воздействие');

set(tit1,'FontName','Courier');

hl=legend('Возмущающее воздействие',0);

set(hl,'FontName','Courier');

grid on;

save Vozmyshyayushee_Vozdeistvie_Discrete_Revers w_discrete_rev

% ------------------------------------------------------------------------%

Zadayushee_Vozdeistvie_Discrete_Revers_Modern.m

% Получение дискретных значений задающего воздействия в обратном времени

% для нахождения вспомогательной функции q(t)

function Zadayushee_Vozdeistvie_Discrete_Revers_Modern(h, T_nach, T_konech)

% ------------------------------------------------------------------------%

% Задающее воздействие

alfa = 0.2;

beta = 10;

H = 0.8;

k = 1;

for t = T_konech: -h : T_nach

X_o_1 = 10*exp(-1/5*t)*t+4/5;

X_o_2 = -2*exp(-1/5*t)*t+10*exp(-1/5*t);

X_o_3 = 2/5*exp(-1/5*t)*t-4*exp(-1/5*t);

X_o_4 = -2/25*exp(-1/5*t)*t+6/5*exp(-1/5*t);

X_o_5 = 2/125*exp(-1/5*t)*t-8/25*exp(-1/5*t);

X_o_discrete_rev(:, k) = [X_o_1; X_o_2; X_o_3; X_o_4; X_o_5];

k = k + 1;

end

figure(2)

t = T_konech : -h : T_nach;

plot(t, X_o_discrete_rev(1,:), 'r-', t, X_o_discrete_rev(1,:)-H, 'LineWidth', 2);

xlabel('t')

tit1 = title('Задающее воздействие');

set(tit1,'FontName','Courier');

hl=legend('Отслеживание зад. возд. на H ','Задающее воздействие',0);

set(hl,'FontName','Courier');

grid on;

save Zadayushee_Vozdeistvie_Discrete_Revers X_o_discrete_rev

% ------------------------------------------------------------------------%

Решение алгебраического уравнения Риккати методом диагонализации

Раздел: Экономико-математическое моделирование
Количество знаков с пробелами: 99279
Количество таблиц: 0
Количество изображений: 156

Скачать

... степеней свободы. Величину критерия Фишера (F-критерий) определяют по формуле: (должно быть). Значимость коэффициентов bi уравнения регрессии определяют по t-критерию (критерии Стьюдента): , . Идентификация объектов управления методом корреляционного анализа Метод корреляционного анализа используется для идентификации объектов управления в том случае, если входные и выходные ...

Скачать

... : - по маслу 20кПа - по воде 20,1кПа Максимальное рабочее давление: - масла 0,5Мпа - воды 0,5МПа Функциональная схема системы регулирования температуры смазочного масла приведена на рис. 9. Она содержит два маслоохладителя параллельно ...

Скачать

... проектирования. Целью проекта является создание программного продукта (ПП), основанного на математическом пакете MatLab, реализующего математическую модель системы управления, построенной на основе оптимального закона, для системы слежения РЛС. Данный проект можно отнести к научно-исследовательской работе, которая принадлежит к типу прикладных, направленных на решение научных проблем с целью ...

Скачать

... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

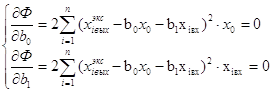
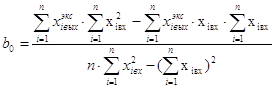
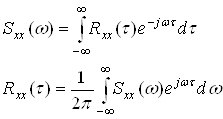
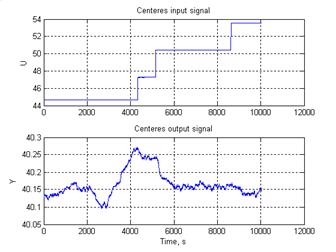
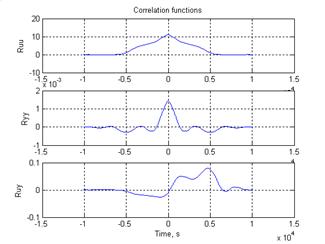
0 комментариев

Разделы

Инфо

Следите за новостями