Навигация
Длина дуги кривой в прямоугольных координатах
11241
знак
0
таблиц
4
изображения
Контрольная работа
По дисциплине:
«Высшая математика»
Тема:
«Длина дуги кривой в прямоугольных координатах»
1. Производная определенного интеграла по переменному верхнему пределу
Сформулируем следующее свойство определенных интегралов:
Пусть функция 
непрерывна на 
. Составим для нее определенный интеграл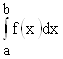 
. Пусть для определенности 
на всем отрезке. Тогда с геометрической точки зрения составленный интеграл не что иное, как площадь криволинейной трапеции с основанием , которая ограничена линией .
Если в рассматриваемом интеграле заменить переменную интегрирования 
на 
, то величина его, очевидно, не изменится. Поэтому в дальнейшем для удобства будем считать, что площадь трапеции определяется интегралом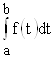 
.
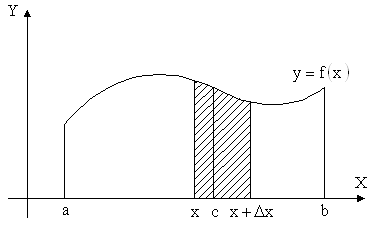
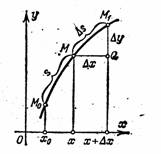
Величина определенного интеграла зависит от значений верхнего и нижнего пределов интегрирования, то есть от длины основания криволинейной трапеции. Рассмотрим поэтому теперь случай, когда нижний предел интеграла фиксирован и равен 
, а верхний может меняться, принимая значения , где 
. В этом случае определенный интеграл будет соответствовать площади криволинейной трапеции, величина которой меняется. Зависеть эта площадь будет от значения , то есть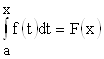 
. Если будет меняться непрерывно, то и площадь трапеции будет меняться непрерывно, то есть 
– непрерывная функция, которую можно дифференцировать.
Теорема. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, у которой переменная интегрирования заменена этим верхним пределом, то есть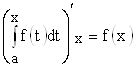 
или 
.
Для вычисления производной проделаем все стандартные операции. Зададим приращение аргументу: 
, что, в свою очередь, приведет к приращению функции: 
. Так как 
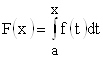, а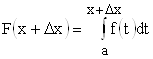 
, то приращение функции определяется выражением:
.
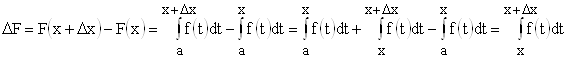Применим к полученному выражению теорему о среднем в определенном интеграле:
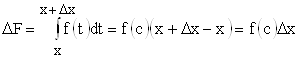, где 
.
Составим отношение 
. Чтобы получить производную 
, перейдем в составленном отношении к пределу: 
. Так как , то при стремлении 
точка 
будет стремиться к . Следовательно, вычисление предела приведет к выражению: .
Из доказанной теоремы следует, что – это первообразная от 
, следовательно, определенный интеграл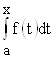 
также является первообразной от , и вычислять его, очевидно, необходимо с помощью тех же приемов, что и неопределенный интеграл.
Похожие работы
... можно показать, что формулы будут справедливы и в случае y!!<0. Параметрическое задание кривой Если кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр: . Тогда (2) Эволюта и эвольвента Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , [si (t) и ci ...
... , повысить интерес к учению; 3) углубить знания, полученные на уроках математики. Ход занятия I. Организационный момент II. Основная часть 1) Лекция об истории изучения плоских кривых [см. гл. I § 1] 2) Задание Ребята, разгадаем с вами кроссворд: ПАСКАЛЬ ПАПИРУС АПОЛЛОНИЙ РОБЕРВАЛЬ АРХИМЕД ГЕОМЕТРИЯ По горизонтали 1. Учёный, считавший, что дуга спирали ...
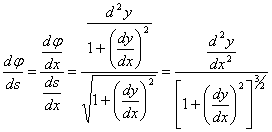
0 комментариев