Навигация
Длина дуги кривой при ее параметрическом задании
11241
знак
0
таблиц
4
изображения
6. Длина дуги кривой при ее параметрическом задании
Рассмотрим теперь случай, когда кривая, длину которой необходимо вычислить, задана параметрически, то есть 
при этом изменение 
от 
до 
приводит к изменению 
от 
до 
. Пусть функции 
и 
непрерывны вместе со своими производными на отрезке 
и при этом 
. Тогда 
, а 
. Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5):
.
В случае пространственной кривой ее параметрическое задание будет выглядеть следующим образом:
Если указанные функции непрерывны вместе со своими производными на отрезке , то можно доказать, что длина данной кривой вычисляется по формуле
.
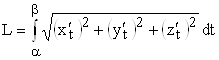7. Длина дуги в полярной системе координат
Если кривая задана в полярной системе координат, то она описывается функцией 
, где 
. Пусть 
непрерывна вместе со своей производной на отрезке .
Перейдем от полярной к прямоугольной системе координат: 
. Но так как , то получаем, что 
. Иначе говоря, и 
выражены через параметр 
, поэтому можно воспользоваться формулой для длины дуги при ее параметрическом задании (п. 6.):
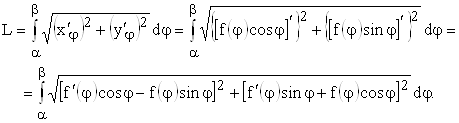
Возведя в квадрат выражения в скобках и выполнив элементарные преобразования, получаем:
.
Обычно данную формулу записывают следующим образом:
.
8. Вычисление объемов тел по известным площадям поперечных сечений
Определенный интеграл в некоторых случаях может быть использован и для вычисления объемов тел. Это можно сделать, когда известны площади всех их поперечных сечений.
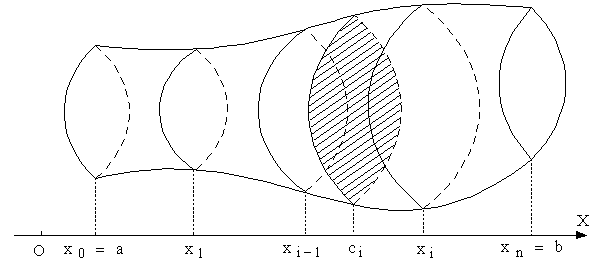
Пусть некоторое тело, объем которого необходимо определить, расположено вдоль оси 
между точками 
и 
. Пусть это тело обладает тем свойством, что известна площадь 
его любого поперечного сечения плоскостью 
, то есть плоскостью, перпендикулярной оси . Так как в общем случае величина этого сечения будет меняться, то 
. В случае, если поверхность тела является гладкой, а тело сплошным, то 
будет непрерывной функцией.
Разобьем отрезок 
точками 
на частичные отрезки и в каждой полученной точке проведем плоскость, перпендикулярную оси . Все тело при этом разобьется на слои, а его объем будет равен сумме объемов всех полученных слоев: 
.
Найдем приближенно величину объема 
-ого слоя 
. Для этого рассмотрим отрезок 
, длина которого равна 
. Возьмем некоторую точку 
и проведем в ней секущую плоскость, перпендикулярную оси . Если достаточно мало, то слой, соответствующий объему , можно практически считать прямым цилиндром с поперечным сечением равным 
. Но в этом случае, как и у кругового цилиндра, 
. Отсюда следует, что
.
Полученное выражение является интегральной суммой. Так как функция по условию непрерывна, то предел этой суммы при 
и 
существует и равен определенному интегралу:
.
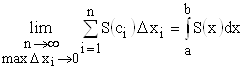Итак, объем тела с известными поперечными сечениями равен:
.
9. Объем тела вращения
Рассмотрим теперь тело, полученное в результате вращения криволинейной трапеции вокруг оси . Пусть основанием этой трапеции является отрезок , расположенный на оси , и она ограничена непрерывной кривой 
. В этом случае в любом сечении полученного тела плоскостью, перпендикулярной оси , будет круг, радиус которого совпадает со значением функции 
в данной конкретной точке. Поэтому площадь сечения будет равна 
.
Подставив данное выражение в формулу для объема тела с известными площадями поперечных сечений, приведенную в предыдущем параграфе, получим:
.
Если трапеция вращается вокруг оси 
, то должна быть задана функция 
на отрезке 
. В этом случае объем тела вращения равен:
.
Литература
1. Крищенко Александр, Канатников Анатолий Аналитическая геометрия: Учебное пособие для студентов высших учебных заведений. Изд-во «Академия», 2009. – 208c.
2. Макарычев Юрий Тригонометрия. Издательство: ПРОСВЕЩЕНИЕ, 2004. – 360 с.
3. Потапов Михаил Задачи по алгебре, тригонометрии и элементарными функциями. Издательство: ЭКЗАМЕН XXI, 2008. – 160 с.
4. Тоом А., Гельфанд И., Львовский С. Тригонометрия. МЦМНО, 2003. – 200 с.
Похожие работы
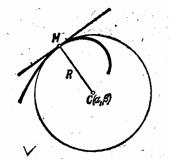
... можно показать, что формулы будут справедливы и в случае y!!<0. Параметрическое задание кривой Если кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр: . Тогда (2) Эволюта и эвольвента Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности. Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например: · параболическая спираль (а - r)2 = bj, · гиперболическая спираль: r = а/j. · Жезл: r2 = a/j · si-ci-cпираль, параметрические уравнения которой имеют вид: , [si (t) и ci ...
... , повысить интерес к учению; 3) углубить знания, полученные на уроках математики. Ход занятия I. Организационный момент II. Основная часть 1) Лекция об истории изучения плоских кривых [см. гл. I § 1] 2) Задание Ребята, разгадаем с вами кроссворд: ПАСКАЛЬ ПАПИРУС АПОЛЛОНИЙ РОБЕРВАЛЬ АРХИМЕД ГЕОМЕТРИЯ По горизонтали 1. Учёный, считавший, что дуга спирали ...
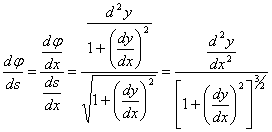
0 комментариев