Навигация
Проверить выполнение предпосылок МНК
3. Проверить выполнение предпосылок МНК.
Предпосылками построения классической линейной регрессионной модели являются четыре условия, известные как условия Гаусса-Маркова.
· В уравнении линейной модели Y=a+b*X+ε слагаемое ε - случайная величина, которая выражает случайный характер результирующей переменной Y.
· Математическое ожидание случайного члена в любом наблюдении равно нулю, а дисперсия постоянна.
· Случайные члены для любых двух разных наблюдений независимы (некоррелированы).
· Распределение случайного члена является нормальными.
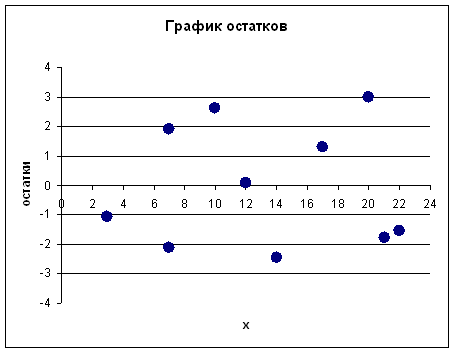
1) Проведем проверку случайности остаточной компоненты по критерию повторных точек.
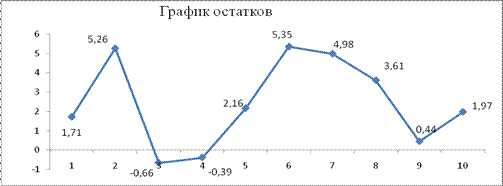
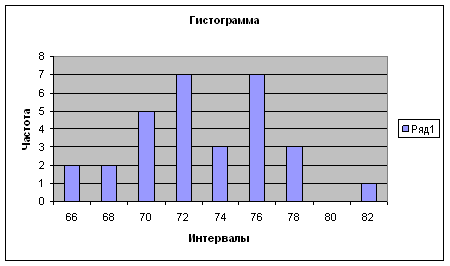
Количество повторных точек определим по графику остатков: p=5
Вычислим критическое значение по формуле:
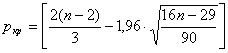 .
.
При ![]() найдем
найдем ![]()
Схема критерия:

Сравним ![]() , следовательно, свойство случайности для ряда остатков выполняется.
, следовательно, свойство случайности для ряда остатков выполняется.
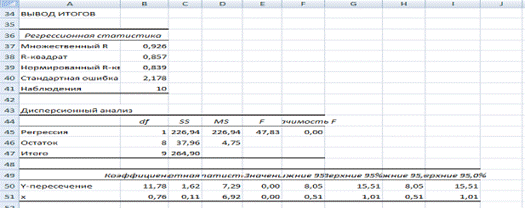
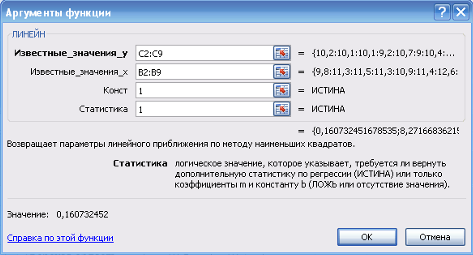
1. Равенство нулю математического ожидания остаточной компоненты для линейной модели, коэффициенты которой определены по МНК, выполняется автоматически. С помощью функции СРЗНАЧ для ряда остатков можно проверить: ![]() .
.
Свойство постоянства дисперсии остаточной компоненты проверим по критерию Гольдфельда–Квандта.
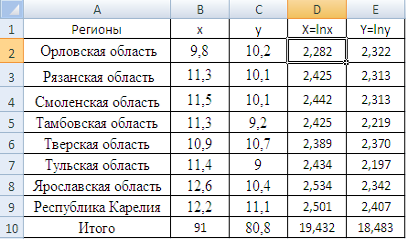
В упорядоченных по возрастанию переменной X исходных данных (![]() ) выделим первые 4 и последние 4 уровня, средние 2 уровня не рассматриваем.
) выделим первые 4 и последние 4 уровня, средние 2 уровня не рассматриваем.
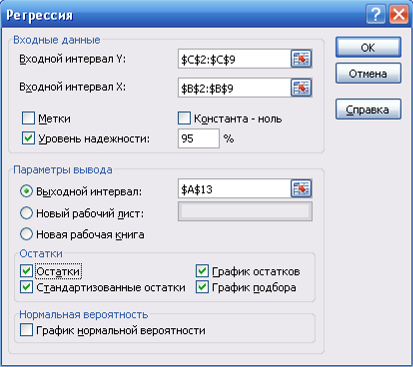
С помощью программы РЕГРЕССИЯ построим модель по первым четырем наблюдениям (регрессия-1), для этой модели остаточная сумма квадратов ![]() .
.
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 107,7894737 | 107,7894737 | 15,67347 | 0,15751 | |
| Остаток | 1 | 6,877192982 | 6,877192982 | |||
| Итого | 2 | 114,6666667 |
С помощью программы РЕГРЕССИЯ построим модель по последним четырем наблюдениям (регрессия-2), для этой модели остаточная сумма квадратов ![]() .
.
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 4,166666667 | 4,166666667 | 0,186916 | 0,707647 | |
| Остаток | 2 | 44,58333333 | 22,29166667 | |||
| Итого | 3 | 48,75 |
Рассчитаем статистику критерия:
![]() .
.
Критическое значение при уровне значимости ![]() и числах степеней свободы
и числах степеней свободы ![]() составляет
составляет ![]() .
.
Схема критерия:
![]()
Сравним ![]() , следовательно, свойство постоянства дисперсии остатков выполняется, модель гомоскедастичная.
, следовательно, свойство постоянства дисперсии остатков выполняется, модель гомоскедастичная.
Похожие работы
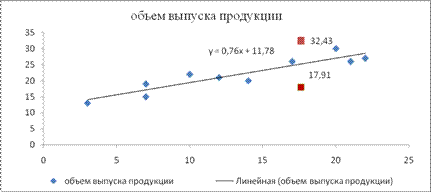
... 106,09 14,97 1,97 3,88 1,53 2,34 сумма 133 219 3211 2161 264,90 392,1 24,43 106,37 0,26 78,80 ср. знач. 13,3 21,9 321,1 216,1 ; Уравнение линейной регрессии имеет вид: у=11,78+0,76х С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб ...
Сумма 133 219 2161 3211 Ср. значение 13,3 21,9 216,1 321,1 Найдем b: Тогда Уравнение линейной регрессии имеет вид: ŷx=11,779+0,761x. Коэффициент регрессии показывает среднее изменение результата с изменением фактора на одну единицу. С увеличением объема капиталовложений на 1 млн. рублей объем выпускаемой продукции увеличится в ...
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... если нужно проверить различается ли разброс данных (дисперсии) у двух выборов. Это может использоваться при сравнении точностей обработки деталей на двух станках, равномерности продаж товара в течении некоторого периода в двух городах и т.д. Для проверки статистической гипотезы, о равенстве дисперсий служит F – критерий Фишера. Основной характеристикой критерия является уровень значимости α, ...
0 комментариев