Проверить выполнение предпосылок МНК
Для проверки независимости уровней ряда остатков используем критерий Дарбина–Уотсона
Представить графически фактические и модальные значения Y точки прогноза
Сравнение моделей по характеристикам: коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Вывод
Навигация
Сравнение моделей по характеристикам: коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Вывод
Методы решения уравнений линейной регрессии
14759
знаков
4
таблицы
6
изображений
9. Сравнение моделей по характеристикам: коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Вывод.
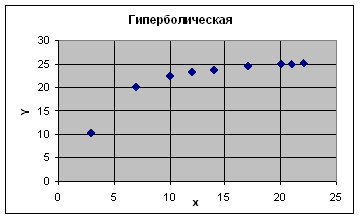
9.1 Гиперболическая модель
Коэффициент детерминации:
=
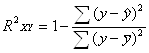Вариация результата Y на 70,9% объясняется вариацией фактора Х.
Коэффициент эластичности:
=
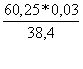= 0,05.
Это означает, что при увеличении фактора Х на 1 % результирующий показатель изменится на 0,05 %.
Бета-коэффициент:
Sx=
=0,01 Sy=
=8,5 
60,25*0,01/8,5=0,07.
Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,07 среднеквадратического отклонения этого показателя.
Средняя относительная ошибка аппроксимации:
отн = 109,7/ 10= 10,97 %.
В среднем расчетные значения 
для гиперболической модели отличаются от фактических значений на 10,97%.
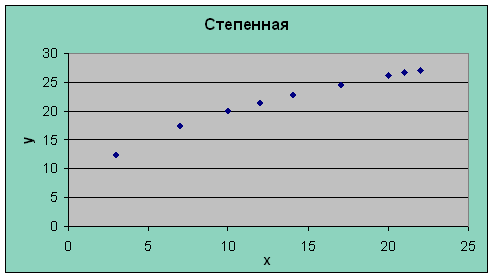
9.2 Степенная модель
Коэффициент детерминации:
=
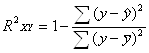Вариация результата Y на 73,6% объясняется вариацией фактора Х. Коэффициент эластичности:
=
= 0,57.
Это означает, что при увеличении факторного признака на 1 % результирующий показатель увеличится на 0,57%.
Бета-коэффициент:
, Sy=
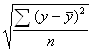и Sx=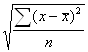
.
Sx=
=0,14 Sy=
=0,10 0,59*0,14/0,1=0,78.
Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,78 среднеквадратического отклонения этого показателя.
отн= 
= 93,77/10 = 9,34%.
В среднем расчетные значения для степенной модели отличаются от фактических значений на 9,34%.
9.3 Показательная модель
Коэффициент детерминации:
=
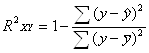Вариация результата Y на 75,7% объясняется вариацией фактора Х. Коэффициент эластичности:
= 28,71.
Это означает, что при росте фактора Х на 1 % результирующий показатель Y изменится на 28,71 %.
Бета-коэффициент:
Sx=
=10,5 Sy==0,10 1,27*10,5/0,10=129,10.
Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 129,1 среднеквадратического отклонения этого показателя.
отн= 91,9/ 10 = 9,19%.
В среднем расчетные значения для показательной модели отличаются от фактических значений на 9,19%.
Вывод
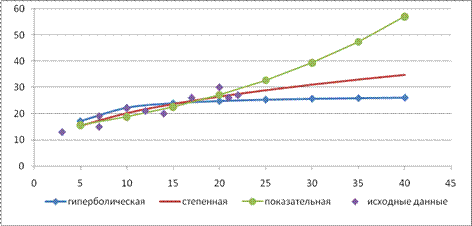
Лучшей из уравнений нелинейной регрессии является показательная: выше коэффициент детерминации, наименьшая относительная ошибка. Модель можно использовать для прогнозирования.
Похожие работы
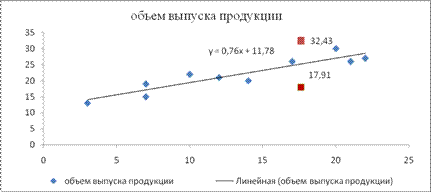
... 106,09 14,97 1,97 3,88 1,53 2,34 сумма 133 219 3211 2161 264,90 392,1 24,43 106,37 0,26 78,80 ср. знач. 13,3 21,9 321,1 216,1 ; Уравнение линейной регрессии имеет вид: у=11,78+0,76х С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб ...
Сумма 133 219 2161 3211 Ср. значение 13,3 21,9 216,1 321,1 Найдем b: Тогда Уравнение линейной регрессии имеет вид: ŷx=11,779+0,761x. Коэффициент регрессии показывает среднее изменение результата с изменением фактора на одну единицу. С увеличением объема капиталовложений на 1 млн. рублей объем выпускаемой продукции увеличится в ...
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... если нужно проверить различается ли разброс данных (дисперсии) у двух выборов. Это может использоваться при сравнении точностей обработки деталей на двух станках, равномерности продаж товара в течении некоторого периода в двух городах и т.д. Для проверки статистической гипотезы, о равенстве дисперсий служит F – критерий Фишера. Основной характеристикой критерия является уровень значимости α, ...
0 комментариев