Навигация
Для проверки независимости уровней ряда остатков используем критерий Дарбина–Уотсона
2. Для проверки независимости уровней ряда остатков используем критерий Дарбина–Уотсона
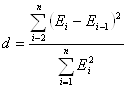 .
.
Предварительно по столбцу остатков с помощью функции СУММКВРАЗН определим ![]() ; используем найденную программой РЕГРЕССИЯ сумму квадратов остаточной компоненты
; используем найденную программой РЕГРЕССИЯ сумму квадратов остаточной компоненты ![]() .
.
Таким образом,
![]()
Схема критерия:

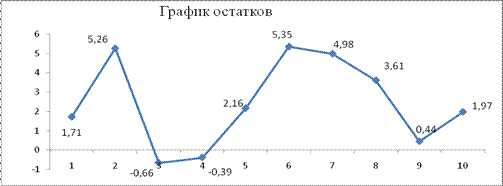
Полученное значение d=2,375, что свидетельствует об отрицательной корреляции. Перейдем к d’=4-d=1,62 и сравним ее с двумя критическими уровнями d1=0,88 и d2=1,32.
D’=1,62 лежит в интервале от d2=1,32 до 2, следовательно, свойство независимости остаточной компоненты выполняются.
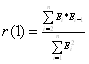
С помощью функции СУММПРОИЗВ найдем для остатков ![]() , следовательно r(1)=2,4869Е-14/148,217=1,67788Е-16.
, следовательно r(1)=2,4869Е-14/148,217=1,67788Е-16.
Критическое значение для коэффициента автокорреляции определяется как отношение ![]() Ön и составляет для данной задачи
Ön и составляет для данной задачи ![]()
Сравнения показывает, что çr(1)= 1,67788Е-16<0,62, следовательно, ряд остатков некоррелирован.
4) Соответствие ряда остатков нормальному закону распределения проверим с помощью ![]() критерия:
критерия:
![]() .
.
С помощью функций МАКС и МИН для ряда остатков определим ![]() ,
, ![]() . Стандартная ошибка модели найдена программой РЕГРЕССИЯ и составляет
. Стандартная ошибка модели найдена программой РЕГРЕССИЯ и составляет ![]() . Тогда:
. Тогда:
![]()
Критический интервал определяется по таблице критических границ отношения ![]() и при
и при ![]() составляет (2,67; 3,57).
составляет (2,67; 3,57).
Схема критерия:
![]()
2,995 ![]() (2,67; 3,57), значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.
(2,67; 3,57), значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.
Проведенная проверка предпосылок регрессионного анализа показала, что для модели выполняются все условия Гаусса–Маркова.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t–критерия Стьюдента (![]() ).
).
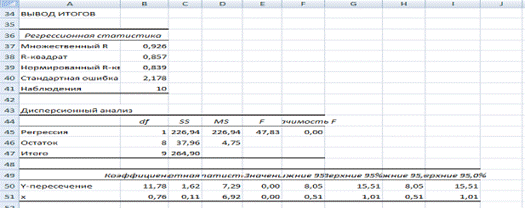
t–статистика для коэффициентов уравнения приведены в таблице 4.
Для свободного коэффициента ![]() определена статистика
определена статистика ![]() .
.
Для коэффициента регрессии ![]() определена статистика
определена статистика ![]() .
.
Критическое значение ![]() найдено для уравнения значимости
найдено для уравнения значимости ![]() и числа степеней свободы
и числа степеней свободы ![]() с помощью функции СТЬЮДРАСПОБР.
с помощью функции СТЬЮДРАСПОБР.
Схема критерия:
![]()
Сравнение показывает:
![]() , следовательно, свободный коэффициент a является значимым.
, следовательно, свободный коэффициент a является значимым.
![]() , значит, коэффициент регрессии b является значимым.
, значит, коэффициент регрессии b является значимым.
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F–критерия Фишера (![]() ), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Коэффициент детерминации R–квадрат определен программой РЕГРЕССИЯ и составляет ![]() .
.
Таким образом, вариация объема выпуска продукции Y на 79,5% объясняется по полученному уравнению вариацией объема капиталовложений X.
Проверим значимость полученного уравнения с помощью F–критерия Фишера.
F–статистика определена программой РЕГРЕССИЯ (таблица 2) и составляет ![]() .
.
Критическое значение ![]() найдено для уровня значимости
найдено для уровня значимости ![]() и чисел степеней свободы
и чисел степеней свободы ![]() ,
, ![]() .
.
Схема критерия:
![]()
Сравнение показывает: ![]() ; следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенной в модель факторной переменной Х.
; следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенной в модель факторной переменной Х.
Для вычисления средней относительной ошибки аппроксимации рассчитаем дополнительный столбец относительных погрешностей, которые вычислим по формуле
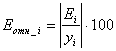
с помощью функции ABS (таблица 5).
ВЫВОД ОСТАТКА | |||
| Наблюдение | Предсказанное Y | Остатки | Отн. Погр-ти |
| 1 | 27,14150943 | 6,858490566 | 20,17% |
| 2 | 29,30660377 | -3,306603774 | 12,72% |
| 3 | 30,02830189 | -6,028301887 | 25,12% |
| 4 | 35,08018868 | 2,919811321 | 7,68% |
| 5 | 35,80188679 | -0,801886792 | 2,29% |
| 6 | 40,13207547 | -0,132075472 | 0,33% |
| 7 | 45,90566038 | -3,905660377 | 9,30% |
| 8 | 45,90566038 | 5,094339623 | 9,99% |
| 9 | 46,62735849 | -1,627358491 | 3,62% |
| 10 | 48,07075472 | 0,929245283 | 1,90% |
По столбцу относительных погрешностей найдем среднее значение ![]() (функция СРЗНАЧ).
(функция СРЗНАЧ).
Схема проверки:
![]()
Сравним: 9,31% < 15%, следовательно, модель является точной.
Вывод: на основании проверки предпосылок МНК, критериев Стьюдента и Фишера и величины коэффициента детерминации модель можно считать полностью адекватной. Дальнейшее использование такой модели для прогнозирования в реальных условиях целесообразно.
6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости ![]() , если прогнозное значение фактора X составит 80% от его максимального значения.
, если прогнозное значение фактора X составит 80% от его максимального значения.
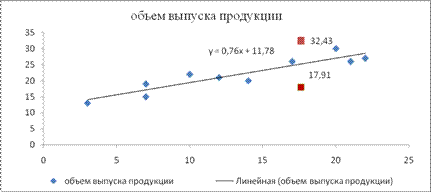
Согласно условию задачи прогнозное значение факторной переменной Х составит 80% от 49, следовательно, ![]() . Рассчитаем по уравнению модели прогнозное значение показателя У:
. Рассчитаем по уравнению модели прогнозное значение показателя У:
![]() .
.
Таким образом, если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции составит около 48 млн. руб.
Зададим доверительную вероятность ![]() и построим доверительный прогнозный интервал для среднего значения Y.
и построим доверительный прогнозный интервал для среднего значения Y.
Для этого нужно рассчитать стандартную ошибку прогнозирования:
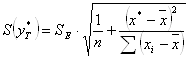
Предварительно подготовим:
- стандартную ошибку модели ![]() (Таблица 2);
(Таблица 2);
- по столбцу исходных данных Х найдем среднее значение ![]() (функция СРЗНАЧ) и определим
(функция СРЗНАЧ) и определим ![]() (функция КВАДРОТКЛ).
(функция КВАДРОТКЛ).
Следовательно, стандартная ошибка прогнозирования для среднего значения составляет:
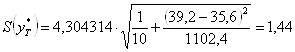
При ![]() размах доверительного интервала для среднего значения
размах доверительного интервала для среднего значения
![]()
Границами прогнозного интервала будут
![]()
![]()
Таким образом, с надежностью 90% можно утверждать, что если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции будет от 45,3 млн. руб. до 50,67 млн. руб.
Похожие работы
... 106,09 14,97 1,97 3,88 1,53 2,34 сумма 133 219 3211 2161 264,90 392,1 24,43 106,37 0,26 78,80 ср. знач. 13,3 21,9 321,1 216,1 ; Уравнение линейной регрессии имеет вид: у=11,78+0,76х С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб ...
Сумма 133 219 2161 3211 Ср. значение 13,3 21,9 216,1 321,1 Найдем b: Тогда Уравнение линейной регрессии имеет вид: ŷx=11,779+0,761x. Коэффициент регрессии показывает среднее изменение результата с изменением фактора на одну единицу. С увеличением объема капиталовложений на 1 млн. рублей объем выпускаемой продукции увеличится в ...
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... если нужно проверить различается ли разброс данных (дисперсии) у двух выборов. Это может использоваться при сравнении точностей обработки деталей на двух станках, равномерности продаж товара в течении некоторого периода в двух городах и т.д. Для проверки статистической гипотезы, о равенстве дисперсий служит F – критерий Фишера. Основной характеристикой критерия является уровень значимости α, ...
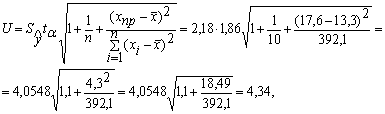
0 комментариев