Навигация
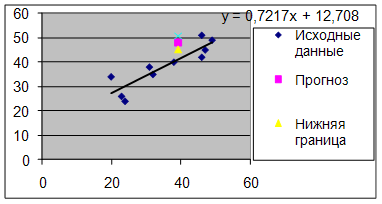
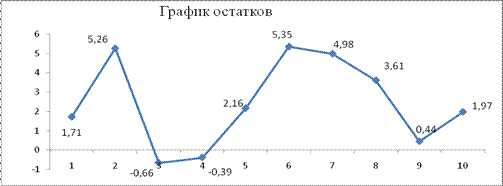
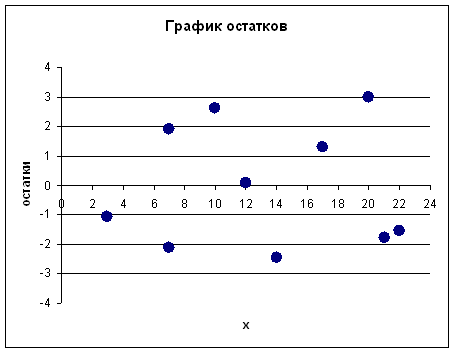
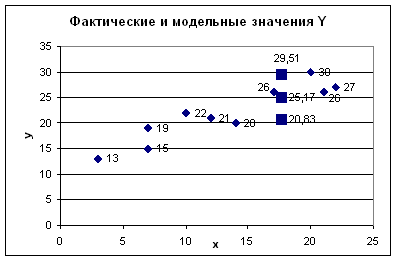
Представить графически фактические и модальные значения Y точки прогноза
7. Представить графически фактические и модальные значения Y точки прогноза.
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции).
Затем с помощью опции Добавить линию тренда… построим линию модели:
тип → линейная; параметры → показывать уравнение на диаграмме.
Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:
Имя → прогноз; значения ![]() ; значения
; значения ![]() ;
;
Имя → нижняя граница; значения ![]() ; значения
; значения ![]() ;
;
Имя → верхняя граница; значения ![]() ; значения
; значения ![]()
8. Составить уравнения нелинейной регрессии: гиперболической; степенной; показательной.
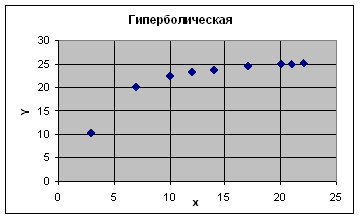
8.1 Гиперболическая модель
Уравнение гиперболической функции:
![]() = a + b/x.
= a + b/x.
Произведем линеаризацию модели путем замены X = 1/x. В результате получим линейное уравнение
![]() = a + bX.
= a + bX.
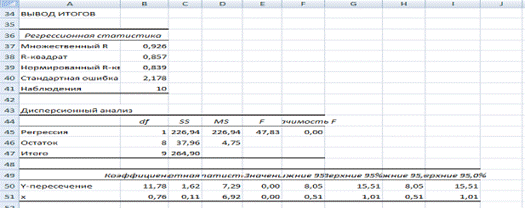
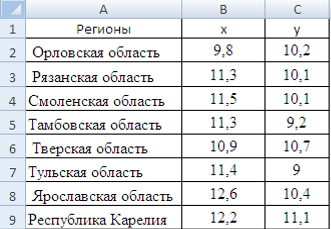
Рассчитаем параметры уравнения по данным таблицы 2.
b =![]() =
=![]()
а = ![]() =38,4+704,48*0,03=60,25.
=38,4+704,48*0,03=60,25.
Получим следующее уравнение гиперболической модели:
![]() = 60,25-704,48/х.
= 60,25-704,48/х.
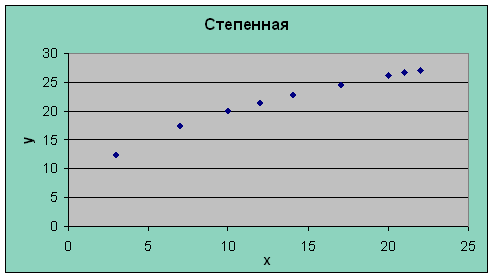
8.2 Степенная модель
Уравнение степенной модели имеет вид: ![]() =аxb
=аxb
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
lg ![]() = lg a + b lg x.
= lg a + b lg x.
Обозначим через
Y=lg ![]() , X=lg x, A=lg a.
, X=lg x, A=lg a.
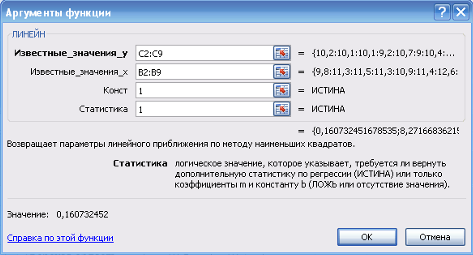
Тогда уравнение примет вид: Y = A + bX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.
b = ![]() =
=![]()
A = ![]() = 1,57-0,64*1,53=0,59
= 1,57-0,64*1,53=0,59
Уравнение регрессии будет иметь вид: Y = 0,59+0,64* Х.
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.
![]() = 100,59* х0,64.
= 100,59* х0,64.
Получим уравнение степенной модели регрессии:
![]() = 3,87* х0,64.
= 3,87* х0,64.
8.3 Показательная модель
Уравнение показательной кривой: ![]() =abx.
=abx.
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
lg ![]() = lg a + x lg b.
= lg a + x lg b.
Обозначим: Y = lg ![]() , B = lg b, A = lg a. Получим линейное уравнение регрессии: Y = A + B x. Рассчитаем его параметры, используя данные таблицы 4.
, B = lg b, A = lg a. Получим линейное уравнение регрессии: Y = A + B x. Рассчитаем его параметры, используя данные таблицы 4.
В =![]() =
=![]()
А =![]() = 1,57-0,01*35,6=1,27
= 1,57-0,01*35,6=1,27
Уравнение будет иметь вид: Y = 1,27+0,01х.
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
![]() =101,27* ( 100,01)х = 18,55*1,02х.
=101,27* ( 100,01)х = 18,55*1,02х.
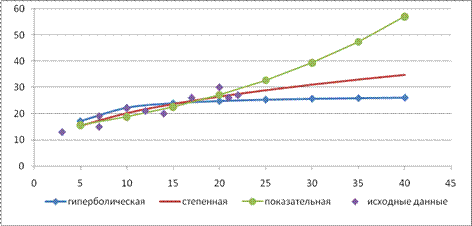
Графики построенных моделей:
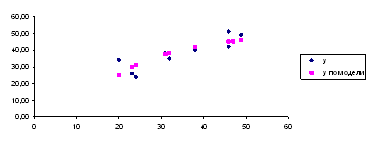
Рис.3. Гиперболическая
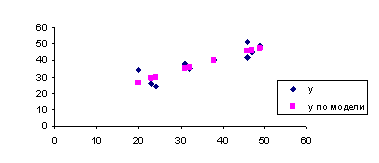
Рис.4. Степенная
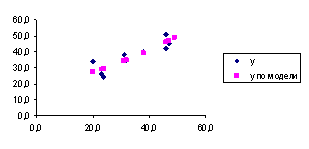
Рис.5. Показательная
Похожие работы
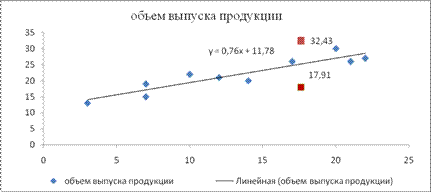
... 106,09 14,97 1,97 3,88 1,53 2,34 сумма 133 219 3211 2161 264,90 392,1 24,43 106,37 0,26 78,80 ср. знач. 13,3 21,9 321,1 216,1 ; Уравнение линейной регрессии имеет вид: у=11,78+0,76х С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб ...
Сумма 133 219 2161 3211 Ср. значение 13,3 21,9 216,1 321,1 Найдем b: Тогда Уравнение линейной регрессии имеет вид: ŷx=11,779+0,761x. Коэффициент регрессии показывает среднее изменение результата с изменением фактора на одну единицу. С увеличением объема капиталовложений на 1 млн. рублей объем выпускаемой продукции увеличится в ...
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... если нужно проверить различается ли разброс данных (дисперсии) у двух выборов. Это может использоваться при сравнении точностей обработки деталей на двух станках, равномерности продаж товара в течении некоторого периода в двух городах и т.д. Для проверки статистической гипотезы, о равенстве дисперсий служит F – критерий Фишера. Основной характеристикой критерия является уровень значимости α, ...
0 комментариев