Математическая модель задачи линейного программирования
Метод допустимого базиса
Решение двойственной задачи
Метод Гомори
Метод ветвей и границ
Метод Баллаша
Метод поиска по координатной сетке с постоянным шагом и метод случайного поиска. Сравнение результатов вычислений
Метод кубической аппроксимации
Лященко И.Н. Линейное и нелинейное программирования / И.Н.Лященко, Е.А.Карагодова, Н.В.Черникова, Н.З.Шор. – К.: «Высшая школа», 1975, 372 с
Навигация
Математическая модель задачи линейного программирования
Линейное и нелинейное программирование
23672
знака
25
таблиц
23
изображения
2.1.2 Математическая модель задачи линейного программирования
AB: 
; 
; 
BC: 
; 
; 
CD: 
; 
; 
DE: 
; 
; 
F: 
; 
; 
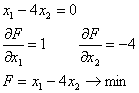
Математическая модель:
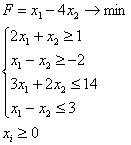
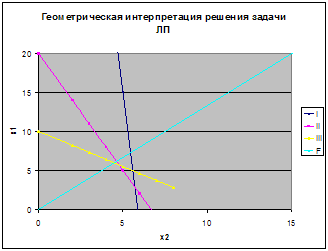
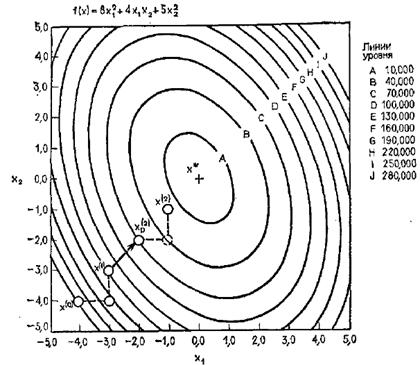
2.1.3 Графический метод
Вычисляем значение целевой функции во всех вершинах симплекса и выбираем из них наименьшее. Это и будет оптимальное решение.
FA = 1
FB = -8
FC = -14
FD = 0
FE = 3
C(2, 4)
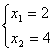
F = -14
2.1.4 Алгебраический метод
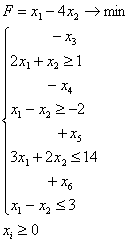
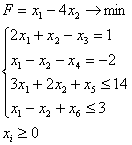
x2, x4, x5, x6 – базисные переменные, x1, x3 – свободные переменные
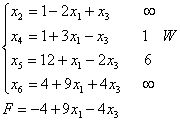
x1↑F↑ x3↑F↓ Выбираем x3 ↔ x4
x2, x3, x5, x6 – базисные переменные, x1, x4 – свободные переменные
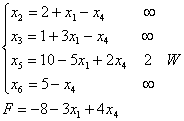
x1↑F↓ x4↑F↑ Выбираем x1 ↔ x5
x1, x2, x3, x6 - базисные переменные, x4, x5 – свободные переменные
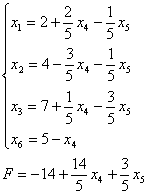
x1↑F↑ x4↑F↑
X=(2, 4, 7, 0, 0, 5)
F = -14
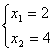
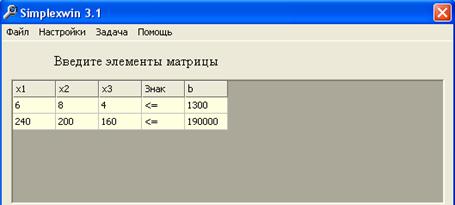
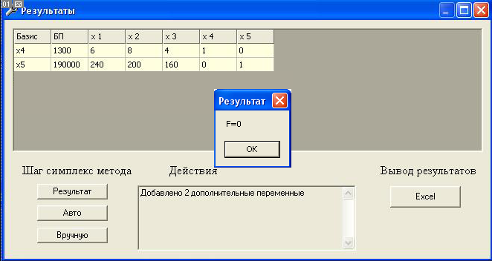
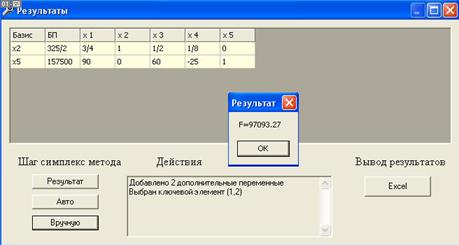
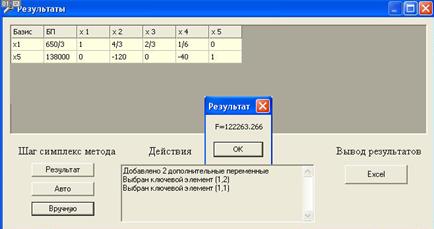
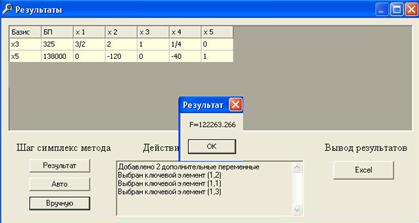
2.1.5 Метод симплекс-таблицы
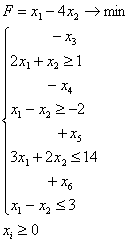
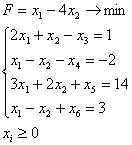
Приведем к каноническому виду:
x2, x4, x5, x6 – базисные переменные, x1, x3 – свободные переменные
| ↑ | ||||||||
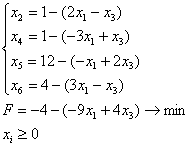
| b | x1 | x3 | ||||||
| x2 | 1 | 2 | -1 | |||||
| 1 | -3 | 1 | ||||||
| ← | x4 | 1 | -3 | 1 | 1 | |||
| 1 | -3 | 1 | ||||||
| x5 | 12 | -1 | 2 | 6 | ||||
| -2 | 6 | -2 | ||||||
| x6 | 4 | 3 | -1 | |||||
| 1 | -3 | 1 | ||||||
| F | -4 | -9 | 4 | |||||
| -4 | 12 | -4 | ||||||
| ↑ | ||||||||
| b | x1 | x4 | ||||||
| x2 | 2 | -1 | 1 | |||||
| 2 | 1/5 | -2/5 | ||||||
| x3 | 1 | -3 | 1 | |||||
| 6 | 3/5 | -6/5 | ||||||
| ← | x5 | 10 | 5 | -2 | 2 | |||
| 2 | 1/5 | -2/5 | ||||||
| x6 | 5 | 0 | 1 | |||||
| 0 | 0 | 0 | ||||||
| F | -8 | 3 | -4 | |||||
| -6 | -3/5 | 6/5 | ||||||
| b | x5 | x4 | ||||||
| x2 | 4 | 1/5 | 3/5 | |||||
| x3 | 7 | 3/5 | -1/5 | |||||
| x1 | 2 | 1/5 | -2/5 | |||||
| x6 | 5 | 0 | 1 | |||||
| F | -14 | -3/5 | -14/5 | |||||
X = (2, 4, 7, 0, 0, 5)
F = -14 
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
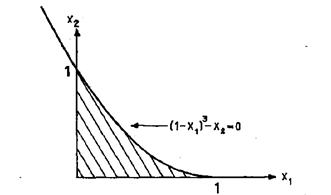
... гиперповерхность наивысшего (наименьшего) уровня: f (x1, x2, …, xn) = h. Указанная точка может находиться как на границе области допустимых решений, так и внутри неё. Процесс нахождения решения задачи нелинейного программирования с использованием ее геометрической интерпретации включает следующие этапы: 1. Находят область допустимых решений задачи, определяемую соотношениями (если она пуста, ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
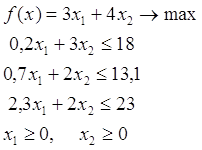
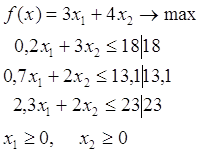
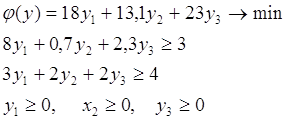
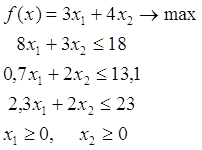
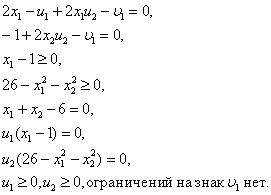
0 комментариев