Навигация
Метод кубической аппроксимации
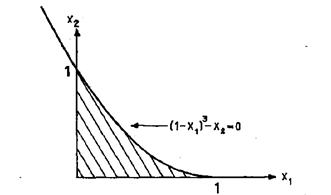
3.2.4 Метод кубической аппроксимации
![]()
![]()
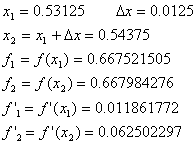
![]()
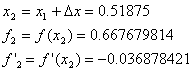
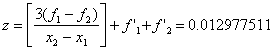
![]()
![]()
![]()
![]()
![]()
3.3 Задача многомерной оптимизации функции
3.3.1 Постановка задачи многомерной оптимизации функции
Минимизировать функцию, применяя следующие методы: нулевого порядка – Хука-Дживса, первого порядка – наискорейшего спуска (Коши), второго порядка – Ньютона, и провести сравнительный анализ методов оптимизации по количеству итераций, необходимых для поиска экстремума при фиксированной точности и начальных координатах поиска X(0)=[-1,-1]T.
![]()
3.3.2 Метод Хука – Дживса
![]()
Итерация 1
1 Исследующий поиск
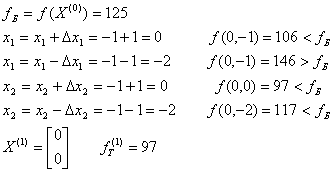
2 Поиск по образцу

Итерация 2
1 Исследующий поиск
![]()
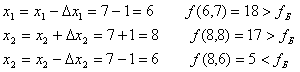
![]()
2 Поиск по образцу
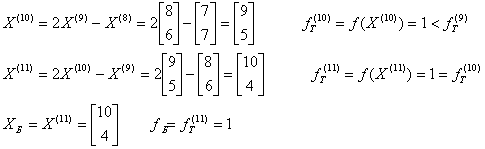
Итерация 3
1 Исследующий поиск
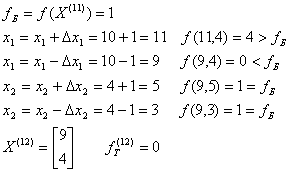
2 Поиск по образцу
![]()
Поиск завершен
![]()
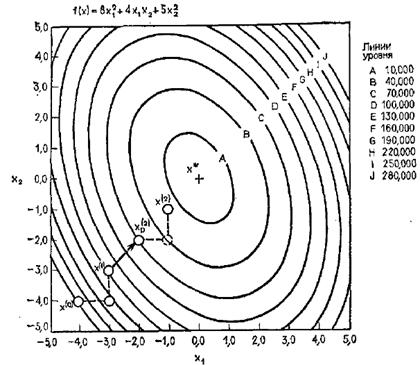
3.3.3 Метод наискорейшего спуска (метод Коши)

![]()
![]()
![]()
Итерация 1. Счет итераций k = 0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
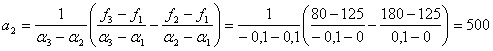
![]()
![]()
Итерация 2. Счет итераций k = 1
![]()
Поиск завершен
![]()
3.3.4 Метод Ньютона

![]()
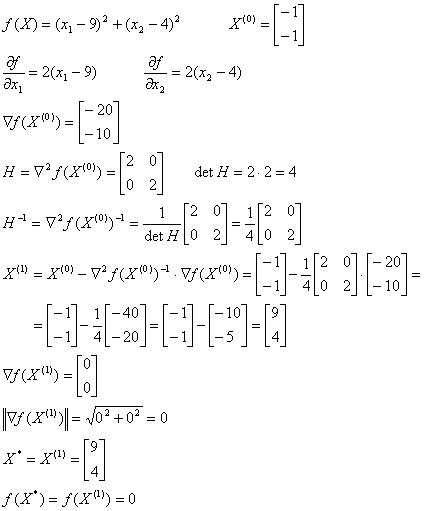
3.3.5 Сравнение результатов вычислений
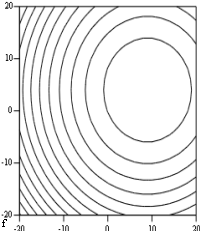
Метод Хука-Дживса сходится за три итерации, при этом происходит вычисление значения функции в 13 точках, всего 38 вычислений. Метод наискорейшего спуска (метод Коши) сходится за одну итерацию, 9 вычислений. Метод Ньютона сходится за одну итерация, 9 вычислений. Методы Коши и Ньютона в данном случае сходятся за одну итерацию, поскольку функция представляет собой функцию для сферы (линии уровня – концентрические окружности) и направление, противоположное градиенту функции, направлено на точку минимума. Из этого можно сделать вывод, что в случае функций такого вида использование метода Хука-Дживса нерационально.
Заключение
Процесс проектирования информационных систем, реализующих новую информационную технологию, непрерывно совершенствуется. В центре внимания инженеров-системотехников оказываются все более сложные системы, что затрудняет использование физических моделей и повышает значимость математических моделей и машинного моделирования систем. Машинное моделирование стало эффективным инструментом исследования и проектирования сложных систем. Актуальность математических моделей непрерывно возрастает из-за их гибкости, адекватности реальным процессам, невысокой стоимости реализации на базе современных ПЭВМ. Все большие возможности предоставляются пользователю, т. е. специалисту по моделированию систем средствами вычислительной техники. Особенно эффективно применение моделирования на ранних этапах проектирования автоматизированных систем, когда цена ошибочных решений наиболее значительна.
Современные вычислительные средства позволили существенно увеличить сложность используемых моделей при изучении систем, появилась возможность построения комбинированных, аналитико-имитационных моделей, учитывающих все многообразие факторов, имеющих место в реальных системах, т. е. использованию моделей, более адекватных исследуемым явлениям.
Библиографический список
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
... гиперповерхность наивысшего (наименьшего) уровня: f (x1, x2, …, xn) = h. Указанная точка может находиться как на границе области допустимых решений, так и внутри неё. Процесс нахождения решения задачи нелинейного программирования с использованием ее геометрической интерпретации включает следующие этапы: 1. Находят область допустимых решений задачи, определяемую соотношениями (если она пуста, ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
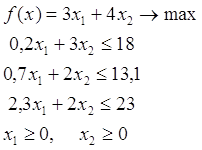
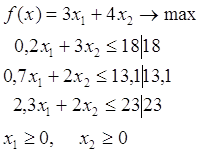





0 комментариев