Навигация
Лященко И.Н. Линейное и нелинейное программирования / И.Н.Лященко, Е.А.Карагодова, Н.В.Черникова, Н.З.Шор. – К.: «Высшая школа», 1975, 372 с
1 Лященко И.Н. Линейное и нелинейное программирования / И.Н.Лященко, Е.А.Карагодова, Н.В.Черникова, Н.З.Шор. – К.: «Высшая школа», 1975, 372 с.
2 Методические указания для выполнения курсового проекта по дисциплине «Прикладная математика» для студентов специальности «Компьютерные системы и сети» дневной и заочной форм обучения / Сост.: И.А.Балакирева, А.В.Скатков– Севастополь: Изд-во СевНТУ, 2003. – 15 с.
3 Методические указания по изучению дисциплины «Прикладная математика», раздел «Методы глобального поиска и одномерной минимизации» / Сост. А.В.Скатков, И.А.Балакирева, Л.А.Литвинова – Севастополь: Изд-во СевГТУ, 2000. – 31с.
4 Методические указания для изучения дисциплины «Прикладная математика» для студентов специальности «Компьютерные системы и сети» Раздел «Решение задач целочисленного линейного программирования» дневной и заочной форм обучения / Сост.: И.А.Балакирева, А.В.Скатков – Севастополь: Изд-во СевНТУ, 2000. – 13 с.
ПРИЛОЖЕНИЕ
А Текст программы глобальной многомерной оптимизации
{$APPTYPE CONSOLE}
program GlobalMinimize;
const
large = 10e99;
var
a1, a2, b1, b2 : real;
a1n, a2n, b1n, b2n : real;
fmin, x1, x2 : real;
alpha, dV, eps : real;
Rho, P : real;
fT, fS : real;
d1, d2, dx1, dx2 : real;
x1min, x2min : real;
i, N : integer;
t : boolean;
function f(x1, x2 : real) : real;
begin
f := 2*sqr(x1) + 2*x1*x2 + sqr(x2) - 2*x1 - 3*x2
end;
function ceil(x : real) : integer;
var a : integer;
begin
a := trunc(x);
if frac(x) > 0 then
a := a + 1;
ceil := a
end;
function max(a, b : real) : real;
begin
if a > b then
max := a
else
max := b
end;
function min(a, b : real) : real;
begin
if a < b then
min := a
else
min := b
end;
begin
randomize;
writeln('Поиск глобального многомерного минимума функции');
writeln('(для курсового проекта по прикладной математике)');
writeln('Автор: Ткаченко К.С. М-21д');
writeln;
writeln('Введите интервал изменения x1');
write(' Введите a1 : '); readln(a1);
write(' Введите b1 : '); readln(b1);
writeln('Введите интервал изменения x2');
write(' Введите a2 : '); readln(a2);
write(' Введите b2 : '); readln(b2);
write('Введите погрешность eps : '); readln(eps);
write('Введите вероятность поиска P : '); readln(P);
write('Введите коэффициент alpha : '); readln(alpha);
write('Введите коэффициент dV : '); readln(dV);
writeln;
writeln('Алгоритм поиска глобального минимума по координатной '+
'сетке с равномерным шагом');
writeln;
t := false; N := 0;
fS := large; fmin := large;
a1n := a1; a2n := a2; b1n := b1; b2n := b2;
repeat
d1 := b1n - a1n; d2 := b2n - a2n;
dx1 := d1 / alpha; dx2 := d2 / alpha;
x1 := a1n; x2 := a2n;
fT := f(x1, x2);
N := N + 1;
if fT < fmin then
begin
fmin := fT;
x1min := x1; x2min := x2;
end;
repeat
repeat
x1 := x1 + dx1; (* Шаг 1 *)
fT := f(x1, x2);
N := N + 1;
if fT < fmin then (* Шаг 2 *)
begin
fmin := fT;
x1min := x1; x2min := x2;
end;
until x1 > b1n; (* Шаг 3 *)
x1 := a1n; x2 := x2 + dx2; (* Шаг 4 *)
fT := f(x1, x2); (* Шаг 5 *)
N := N + 1;
if fT < fmin then (* Шаг 6 *)
begin
fmin := fT;
x1min := x1; x2min := x2;
end;
until x2 > b2n; (* Шаг 7 *)
if abs(fS - fmin) > eps then (* Шаг 8 *)
begin (* Шаг 9 *)
fS := fmin;
a1n := max(x1min-dx1,a1n); b1n := min(x1min+dx1,b1n);
a2n := max(x2min-dx2,a2n); b2n := min(x2min+dx2,b2n);
end
else t := true; (* Шаг 10 *)
until t;
writeln('Число испытаний N = ', N);
writeln('fmin = ', fmin : 6 : 3);
writeln('x1min = ', x1min : 6 : 3);
writeln('x2min = ', x2min : 6 : 3);
writeln;
writeln('Алгоритм поиска глобального минимума функции '+
'методом случайного поиска');
writeln;
fmin := large;
x1min := fmin; x2min := fmin;
d1 := b1 - a1; d2 := b2 - a2;
Rho := dV/(d1 * d2);
N := ceil(ln(1 - P)/ln(1 - Rho));
writeln('Число испытаний N = ', N);
for i := 1 to N do (* Шаги 1, 2 *)
begin
x1 := a1 + random * d1; (* Шаги 3, 4 *)
x2 := a2 + random * d2;
fT := f(x1, x2); (* Шаг 5 *)
if fT < fmin then (* Шаг 6 *)
begin
fmin := fT;
x1min := x1;
x2min := x2
end;
end; (* Шаг 7 *)
writeln('fmin = ', fmin : 6 : 3);
writeln('x1min = ', x1min : 6 : 3);
writeln('x2min = ', x2min : 6 : 3);
end.
Б. Результаты работы программы
Поиск глобального многомерного минимума функции
(для курсового проекта по прикладной математике)
Автор: Ткаченко К.С. М-21д
Введите интервал изменения x1
Введите a1 : -5
Введите b1 : 5
Введите интервал изменения x2
Введите a2 : -5
Введите b2 : 5
Введите погрешность eps : 0.0001
Введите вероятность поиска P : 0.95
Введите коэффициент alpha : 20
Введите коэффициент dV : 1
Алгоритм поиска глобального минимума по координатной сетке с равномерным шагом
Число испытаний N = 905
fmin = -2.500
x1min = -0.500
x2min = 2.000
Алгоритм поиска глобального минимума функции методом случайного поиска
Число испытаний N = 299
fmin = -2.469
x1min = -0.677
x2min = 2.173
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
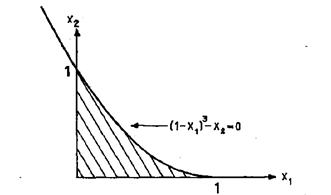
... гиперповерхность наивысшего (наименьшего) уровня: f (x1, x2, …, xn) = h. Указанная точка может находиться как на границе области допустимых решений, так и внутри неё. Процесс нахождения решения задачи нелинейного программирования с использованием ее геометрической интерпретации включает следующие этапы: 1. Находят область допустимых решений задачи, определяемую соотношениями (если она пуста, ...
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
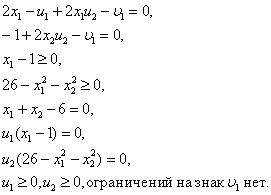





0 комментариев