Навигация
Плотность распределения вероятности
25495
знаков
9
таблиц
1
изображение
1. Плотность распределения вероятности.
2. Параметры 
и 
.
3. Математическое ожидание, дисперсию, среднее квадратическое отклонение спроса.
4. Вероятность того, что в наудачу выбранном микрорайоне спрос находится в пределах от значения 
до 
.
5. Размер спроса, который для случайного выбранного микрорайона может быть превзойден с вероятностью 
.
Параметры 
(в млн. руб), приводятся в таблице 5.
Таблица 5
| Значения параметров | ||||
|
|
|
|
|
|
| 1 | 2 | 2 | 3 | 0,5 |
Решение.
1. Плотность распределения вероятностей является производной функции распределения вероятностей, поэтому:
2.Найдем параметр . Функция распределения 
обладает следующим свойством:
=1. Вычислим предел
=
.
Отсюда 
=1.
Далее определим параметр 
. Интеграл от плотности вероятности по области реализации случайной величины равен единице. В соответствии с условиями задачи спрос как случайная величина изменяется в пределах от 
до 
. Поэтому, находя несобственный интеграл, имеем
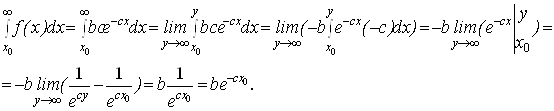
Таким образом, =
.
3.Вычислим математическое ожидание спроса через плотность распределения (с учетом того, что =) как несобственный интеграл:
.
Найдем интеграл методом интегрирования по частям. Пусть 
.
Тогда
.
Применяя формулу интегрирования по частям, получим
.
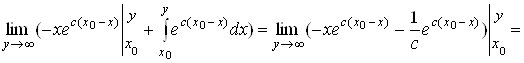
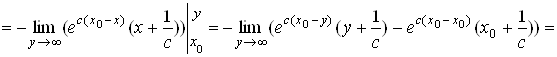
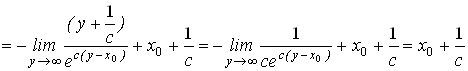Подставив в полученное выражение численные значения параметров, найдем:
По формуле
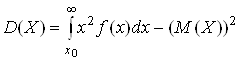
определим дисперсию спроса. Вначале вычислим несобственный интеграл
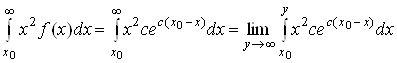
также методом интегрирования по частям. Пусть 
. Тогда
,
.
Последний интеграл уже найден при вычислении 
, поэтому можно записать:
.
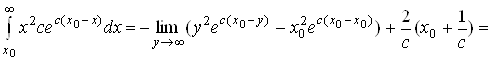
Отсюда окончательно получаем:
.
После подстановки численных значений параметров, находим
Среднеквадратическое отклонение вычисляется как квадратный корень из дисперсии:
Похожие работы
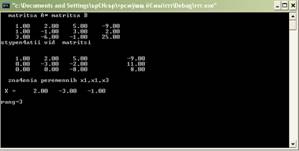
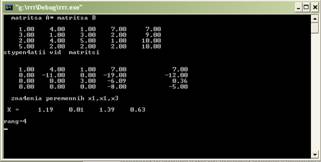
... , с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее. Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, ...
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...
... в пути 1 ч (7 ч 35 мин. – 6 ч 35 мин.= 1ч). Получаем уравнение: 2,5V1 +V2 =180. Таким образом, имеем систему двух уравнений с двумя неизвестными: , откуда V1=40 км/ч, V2=80 км/ч. Ответ: 40 км/ч, 80 км/ч. 4. Линейные неравенства с одной переменной. Если переменной х придать какое-либо числовое значение, то мы получим числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, ...
... , придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д. Если работа в поисках более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки будет успешна, то практическая значимость будет очевидна. Список использованной литературы 1. Алгебра 8 класс. Н.Я. Виленкин. Москва, ...
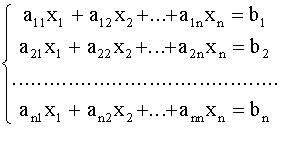
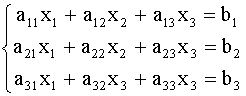
0 комментариев