Навигация
Вероятность нахождения случайной величины в заданном интервале можно найти, используя функцию распределения
4. Вероятность нахождения случайной величины в заданном интервале можно найти, используя функцию распределения
![]()
При ![]() получаем
получаем
![]()
Подставляя численные значения параметров, имеем:
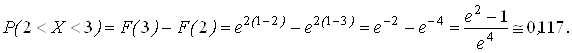
Величина ![]() , определяемая равенством
, определяемая равенством ![]() , называется квантилем порядка
, называется квантилем порядка ![]() . В задаче требуется найти
. В задаче требуется найти ![]() . Запишем необходимое равенство:
. Запишем необходимое равенство: ![]() или
или ![]() . Логарифмируя последнее равенство
. Логарифмируя последнее равенство ![]() , найдем
, найдем
![]() .
.
При ![]() =0,5 получаем:
=0,5 получаем:
![]()
Таким образом, с вероятностью 0,5 спрос в случайно выбранном микрорайоне будет больше 1,35 (млн. руб).
Задача для контрольной работы
Функция распределения годовых доходов лиц, облагаемых налогом, описывается выражением:

Требуется найти:
1. Плотность распределения вероятности.
2. Параметры ![]() и
и ![]() .
.
3. Математическое ожидание, дисперсию, среднее квадратическое отклонение годового дохода.
4. Вероятность того, что у наудачу выбранного налогоплательщика годовой доход находится в пределах от значения ![]() до
до ![]() .
.
5. Размер годового дохода, который для случайного выбранного налогоплательщика может быть превзойден с вероятностью ![]() .
.
Параметры ![]() для различных вариантов заданий приводятся в таблице 6.
для различных вариантов заданий приводятся в таблице 6.
Таблица 6
| Параметры | Номер варианта | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|
| 200 | 250 | 300 | 350 | 360 | 370 | 380 | 390 | 400 | 410 |
|
| 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 |
|
| 210 | 280 | 350 | 400 | 380 | 390 | 410 | 420 | 425 | 440 |
|
| 230 | 300 | 400 | 480 | 400 | 420 | 430 | 450 | 460 | 500 |
|
| 0,3 | 0,35 | 0,4 | 0,45 | 0,5 | 0,55 | 0,6 | 0,55 | 0,65 | 0,7 |
Тема 5. Математическая статистика
Задача. При оценке свойств картофеля было обследовано 10 проб и получены следующие значения содержания крахмала ![]() :
:
Таблица 7
| Содержание крахмала, % | |||||||||
|
|
|
|
|
|
|
|
|
|
|
| 5,2 | 5,8 | 5,7 | 6,0 | 5,9 | 5,3 | 4,9 | 5,1 | 5,3 | 5,8 |
Требуется:
1. Определить выборочное среднее ![]() , выборочную дисперсию
, выборочную дисперсию ![]() , среднее квадратическое отклонение
, среднее квадратическое отклонение ![]() , исправленные дисперсию
, исправленные дисперсию ![]() и среднее квадратическое отклонение
и среднее квадратическое отклонение ![]() для величины
для величины ![]() .
.
2. Полагая, что изменчивость величины ![]() описывается законом нормального распределения, найти доверительные интервалы для ожидаемого среднего значения
описывается законом нормального распределения, найти доверительные интервалы для ожидаемого среднего значения ![]() и ожидаемого среднего квадратического отклонения
и ожидаемого среднего квадратического отклонения ![]() содержания крахмала с заданной надежностью
содержания крахмала с заданной надежностью ![]() , а также вероятность того, что величина содержания крахмала
, а также вероятность того, что величина содержания крахмала ![]() в выбранной наудачу пробе окажется в пределе от
в выбранной наудачу пробе окажется в пределе от ![]() до
до ![]() .
.
3. Проверить на уровне значимости ![]() нулевую гипотезу
нулевую гипотезу ![]() :
:![]() при конкурирующей гипотезе
при конкурирующей гипотезе ![]() :
: ![]() .
.
Задачу решить для следующих значений параметров ![]() ,
, ![]() ,
, ![]() .
.
Решение.1.Выборочное среднее при объеме выборки n=10 находится по формуле
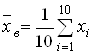 .
.
Подставляя в формулу значения ![]() из таблицы 7, получим
из таблицы 7, получим
![]() =5,5 (%).
=5,5 (%).
Для вычисления выборочной дисперсии используется формула
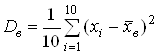 .
.
Составим следующую вспомогательную таблицу, куда внесем отклонения ![]() и их квадраты
и их квадраты ![]() .
.
Таблица 8
| Содержание крахмала в пробе, % |
|
|
| 5,2 | -0,3 | 0,09 |
| 5,8 | 0,3 | 0,09 |
| 5,7 | 0,2 | 0,04 |
| 6,0 | 0,5 | 0,25 |
| 5,9 | 0,4 | 0,16 |
| 5,3 | -0,2 | 0,04 |
| 4,9 | -0,6 | 0,36 |
| 5,1 | -0,4 | 0,16 |
| 5,3 | -0,2 | 0,04 |
| 5,8 | 0,3 | 0,09 |
|
| - | 1,32 |
По данным таблицы 8 определим выборочное среднее
![]()
Выборочное среднее квадратическое отклонение находится:
![]()
Исправленную дисперсию ![]() находят для малых значений n (n<30) по значению
находят для малых значений n (n<30) по значению ![]() :
:
![]()
Исправленное стандартное отклонение ![]() вычисляют путем извлечения квадратного корня из
вычисляют путем извлечения квадратного корня из
![]() :
: ![]()
Для оценки математического ожидания ![]() нормально распределенного признака
нормально распределенного признака ![]() по выборочной средней
по выборочной средней ![]() при неизвестном среднем квадратическом отклонении
при неизвестном среднем квадратическом отклонении ![]() генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал
![]()
где ![]() =2,26 находим по таблице ([2], приложение 3) по заданным n=10 и
=2,26 находим по таблице ([2], приложение 3) по заданным n=10 и ![]() =0,95.
=0,95.
Вычислим
![]() Тогда
Тогда
![]() или
или ![]()
Оценкой среднего квадратического отклонения ![]() нормально распределенного количественного признака
нормально распределенного количественного признака ![]() по исправленному выборочному среднему квадратическому отклонению
по исправленному выборочному среднему квадратическому отклонению ![]() служат доверительные интервалы
служат доверительные интервалы
![]() при
при ![]()
![]() при
при ![]()
где ![]() находят по таблице ([2], приложение 4) по заданным значениям n=10 и
находят по таблице ([2], приложение 4) по заданным значениям n=10 и ![]() =0,95. В данном случае
=0,95. В данном случае ![]() и используется первая формула:
и используется первая формула:
![]() или
или ![]()
Чтобы найти вероятность того, что величина содержания крахмала ![]() в выбранной наудачу пробе окажется в пределе от
в выбранной наудачу пробе окажется в пределе от ![]() до
до ![]() воспользуемся точечными оценками параметров нормального распределения
воспользуемся точечными оценками параметров нормального распределения ![]() и
и ![]() в формуле:
в формуле:
![]() .
.
Учитывая нечетность функции Лапласа ![]() , имеем ([2], приложение 2)
, имеем ([2], приложение 2)
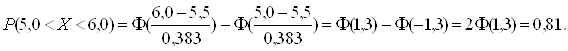
3. Для того, чтобы при заданном уровне значимости ![]() , проверить нулевую гипотезу
, проверить нулевую гипотезу ![]() :
:![]() о равенстве неизвестной генеральной средней
о равенстве неизвестной генеральной средней ![]() гипотетическому значению
гипотетическому значению ![]() при конкурирующей гипотезе
при конкурирующей гипотезе ![]() :
: ![]() , надо вычислить наблюдаемое значение статистического критерия
, надо вычислить наблюдаемое значение статистического критерия
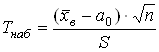
и по таблице критических точек распределения Стьюдента по заданному значению![]() и числу степеней свободы k=n-1 найти критическую точку
и числу степеней свободы k=n-1 найти критическую точку ![]() . Если справедливо неравенство
. Если справедливо неравенство ![]() , то оснований отвергнуть нулевую гипотезу не имеется. В противном случае нулевую гипотезу отвергают.
, то оснований отвергнуть нулевую гипотезу не имеется. В противном случае нулевую гипотезу отвергают.
Найдем наблюдаемое значение критерия
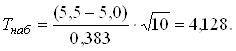
В таблице критических точек распределения Стьюдента ([2], приложение 6) по значению ![]() =0,05 и числу степеней свободы k = n-1 =9 находим
=0,05 и числу степеней свободы k = n-1 =9 находим ![]() =2,26. Так как выполняется неравенство
=2,26. Так как выполняется неравенство ![]() , то нулевая гипотеза отвергается и выборочная средняя
, то нулевая гипотеза отвергается и выборочная средняя ![]() =5,5 значимо отличается от генеральной средней
=5,5 значимо отличается от генеральной средней ![]() =5,0. Заметим, что если бы проверялась нулевая гипотеза для
=5,0. Заметим, что если бы проверялась нулевая гипотеза для ![]() =5,3, то наблюдаемое значение критерия было бы
=5,3, то наблюдаемое значение критерия было бы ![]() =1,65 и нулевую гипотезу не было бы оснований отвергать и
=1,65 и нулевую гипотезу не было бы оснований отвергать и ![]() незначимо отличалась бы от
незначимо отличалась бы от ![]() .
.
Задача для контрольной работы
При анализе производительности труда ![]() (тыс. руб) на одного работника за отчетный период было обследовано десять магазинов торга.
(тыс. руб) на одного работника за отчетный период было обследовано десять магазинов торга.
Требуется:
1. Определить выборочное среднее ![]() , выборочную дисперсию
, выборочную дисперсию ![]() , среднее квадратическое отклонение
, среднее квадратическое отклонение ![]() , исправленные дисперсию
, исправленные дисперсию ![]() и среднее квадратическое отклонение
и среднее квадратическое отклонение ![]() .
.
2. Полагая, что изменчивость величины ![]() описывается законом нормального распределения, найти доверительные интервалы для ожидаемого среднего значения
описывается законом нормального распределения, найти доверительные интервалы для ожидаемого среднего значения ![]() и ожидаемого среднего квадратического отклонения
и ожидаемого среднего квадратического отклонения ![]() производительности труда с заданной надежностью
производительности труда с заданной надежностью ![]() , а также вероятность того, что величина производительности труда
, а также вероятность того, что величина производительности труда ![]() в выбранном наудачу магазине окажется в пределе от
в выбранном наудачу магазине окажется в пределе от ![]() до
до ![]() .
.
3. Проверить на уровне значимости ![]() нулевую гипотезу
нулевую гипотезу ![]() :
:![]() при конкурирующей гипотезе
при конкурирующей гипотезе ![]() :
: ![]() .
.
Выработка на одного работника ![]() (тыс. руб) и параметры
(тыс. руб) и параметры ![]() для различных вариантов заданий приводятся в таблице 9.
для различных вариантов заданий приводятся в таблице 9.
Таблица 9
| Номер варианта | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Выработка на одного работника |
| 3,9 | 4,6 | 5,6 | 4,7 | 4,2 | 5,1 | 4,4 | 4,7 | 4,5 | 4,1 |
|
| 4,0 | 6,2 | 4,5 | 3,8 | 5,9 | 4,8 | 4,2 | 4,8 | 3,6 | 3,3 | |
|
| 3,8 | 5,6 | 3,8 | 4,8 | 6,4 | 5,6 | 3,7 | 5,3 | 4,7 | 3,2 | |
|
| 4,2 | 4,6 | 4,9 | 4,5 | 5,4 | 6,7 | 3,5 | 4,9 | 3,8 | 3,1 | |
|
| 4,6 | 6,3 | 4,8 | 5,3 | 6,2 | 5,8 | 4,0 | 5,7 | 4,2 | 2,9 | |
|
| 4,5 | 5,0 | 5,8 | 5,2 | 6,3 | 4,9 | 4,6 | 5,0 | 5,1 | 4,2 | |
|
| 4,8 | 4,3 | 5,1 | 6,1 | 5,3 | 5,0 | 4,5 | 6,1 | 4,6 | 4,8 | |
|
| 4,1 | 5,2 | 6,7 | 5,8 | 5,5 | 5,5 | 4,8 | 6,0 | 4,3 | 3,5 | |
|
| 5,0 | 4,4 | 6,4 | 3,8 | 6,4 | 6,1 | 3,8 | 4,9 | 4,4 | 4,4 | |
|
| 4,9 | 6,3 | 3,9 | 4,7 | 5,7 | 5,8 | 4,1 | 5,2 | 5,0 | 5,0 | |
| Параметр |
| 3,5 | 4,0 | 4,5 | 5,5 | 4,5 | 5,5 | 4,0 | 5,0 | 4,0 | 4,0 |
|
| 4,0 | 5,5 | 5,0 | 6,0 | 5,5 | 6,5 | 4,5 | 5,5 | 5,0 | 5,0 | |
|
| 5,2 | 6,0 | 6,2 | 5,8 | 6,5 | 6,6 | 5,2 | 6,0 | 5,0 | 5,0 | |
Правила выполнения и оформления контрольной работы
1. Выбор вариантов осуществляется в соответствии с последней цифрой учебного шифра студента (например, если последняя цифра «3», то выполняется вариант номер 3, если - «0», то - вариант номер 10).
2. Контрольная работа пишется чернилами любого цвета (кроме красного) в тонкой тетради, для замечаний рецензента оставляются поля. На обложке тетради указывают фамилию, имя, отчество студента, номер студенческой группы, учебный шифр (серия и номер зачетной книжки), название кафедры, наименование дисциплины и номер контрольной работы, а также домашний адрес.
3. Решение задач следует располагать в порядке следования номеров, указанных в задании, сохраняя номера задач. Условия задач выписывать обязательно. Если несколько задач имеют общую формулировку, то при переписывании общие условия заменяют конкретными данными.
4. Решения задач требуется оформлять аккуратно, подробно объясняя все действия и используемые формулы. В конце работы приводится список использованной литературы, указывается дата выполнения работы и ставится подпись исполнителя.
Литература
Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа,1977.
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1975.
Высшая математика для экономистов. Под ред. Н. Ш. Кремера. М.: Банки и биржи, 1997.
Талызин В.А. Контрольная работа по высшей математике. Казань: КИ МГУК, 1998.
Похожие работы
... , с помощью которых в последующем решение систем линейных уравнений станет намного проще, понятнее и быстрее. Цель моей работы заключается в том, чтобы изучить различные способы решения систем линейных уравнений для применения их на практике. Для достижения любой цели необходимо выполнить какие-то определенные задачи. Мне нужно выполнить следующие задачи: исследовать литературу по темам матриц, ...
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...
... в пути 1 ч (7 ч 35 мин. – 6 ч 35 мин.= 1ч). Получаем уравнение: 2,5V1 +V2 =180. Таким образом, имеем систему двух уравнений с двумя неизвестными: , откуда V1=40 км/ч, V2=80 км/ч. Ответ: 40 км/ч, 80 км/ч. 4. Линейные неравенства с одной переменной. Если переменной х придать какое-либо числовое значение, то мы получим числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, ...
... , придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д. Если работа в поисках более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки будет успешна, то практическая значимость будет очевидна. Список использованной литературы 1. Алгебра 8 класс. Н.Я. Виленкин. Москва, ...
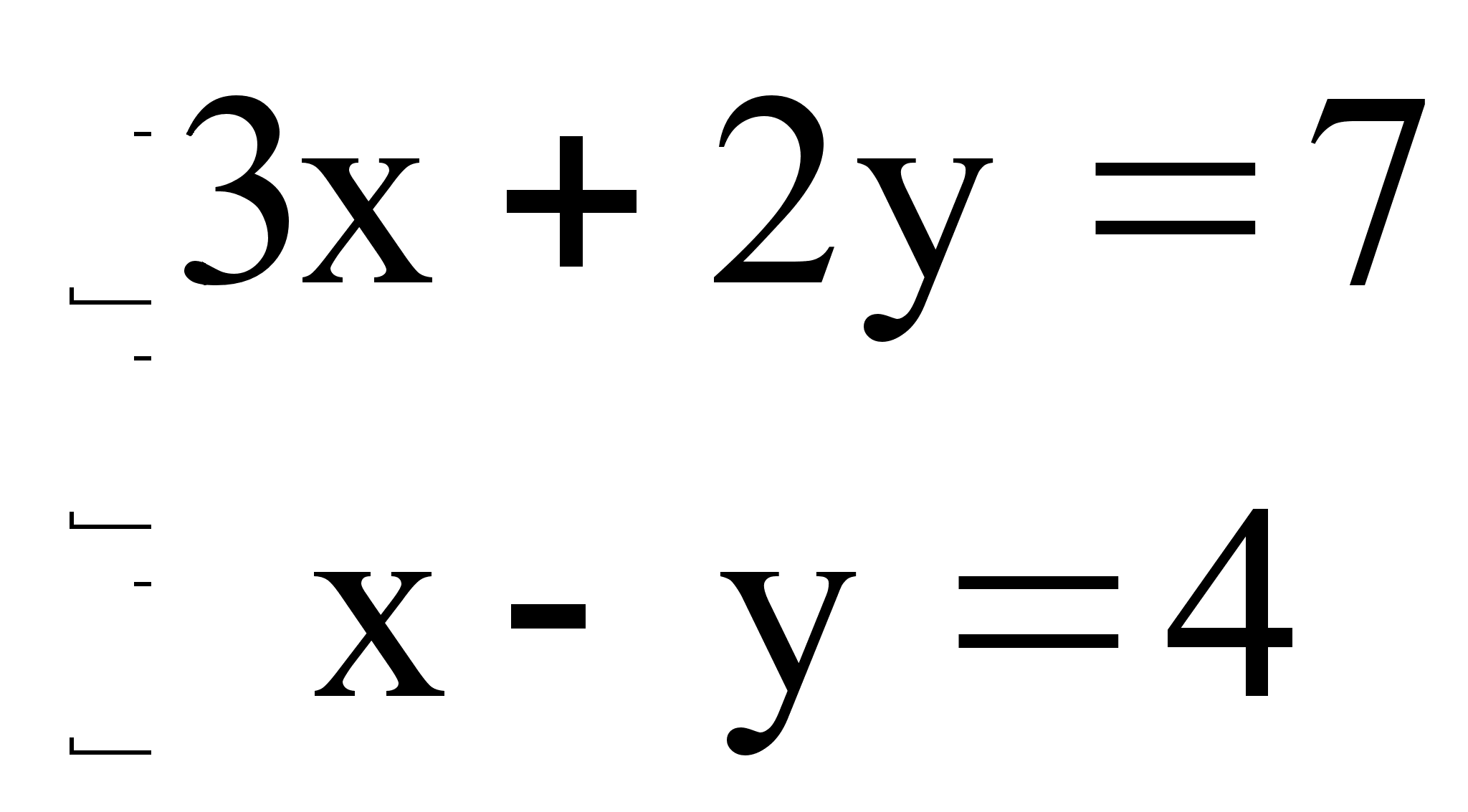
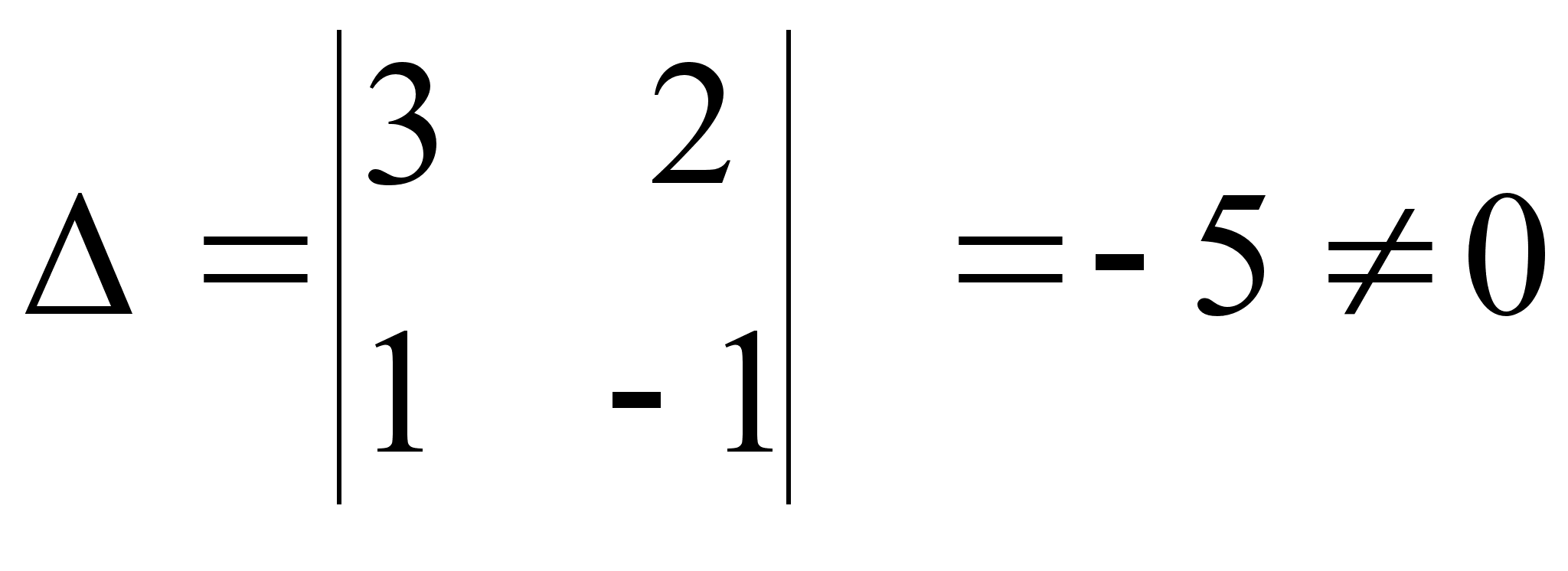
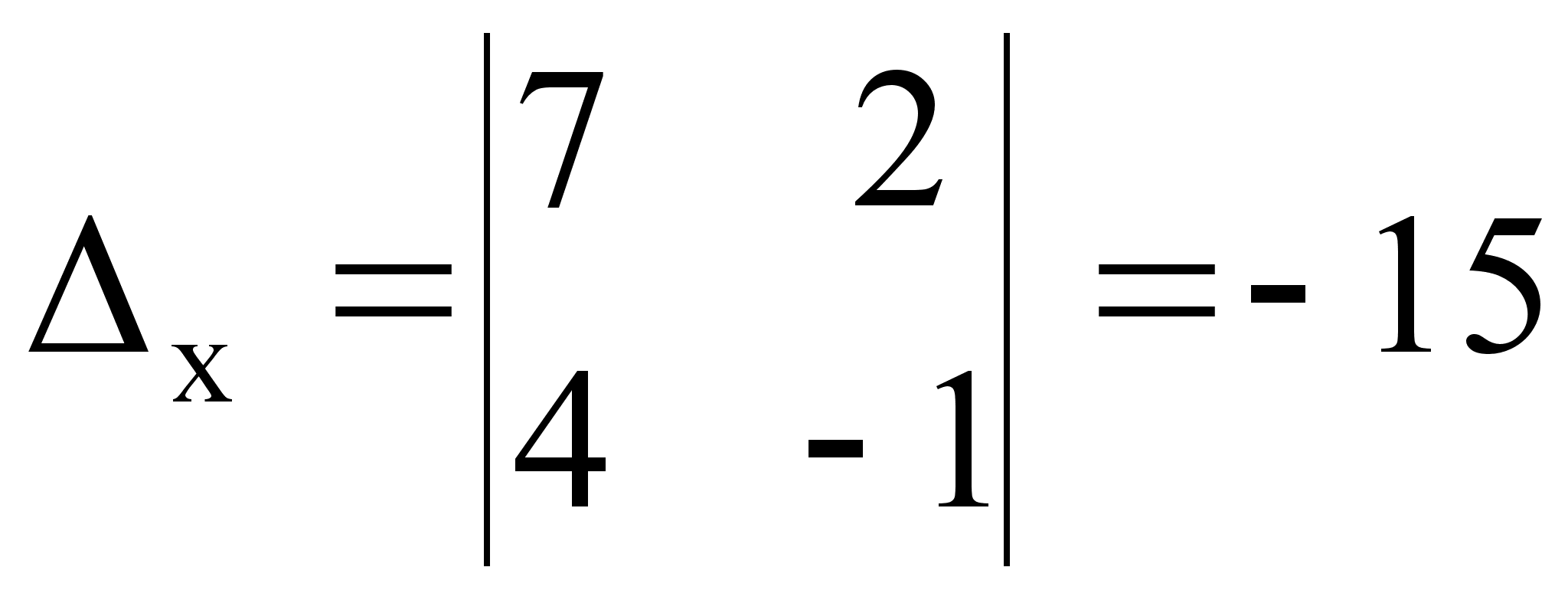
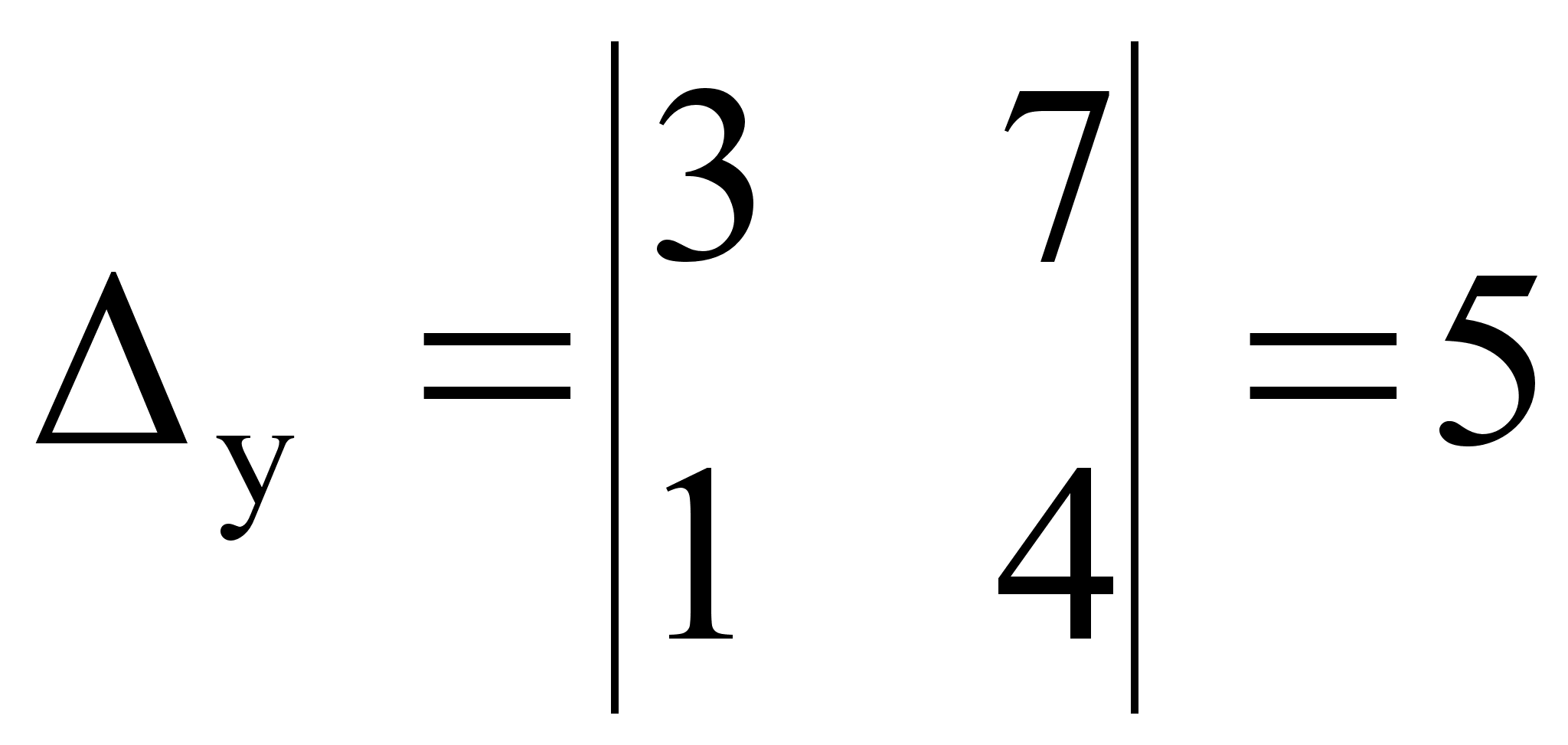
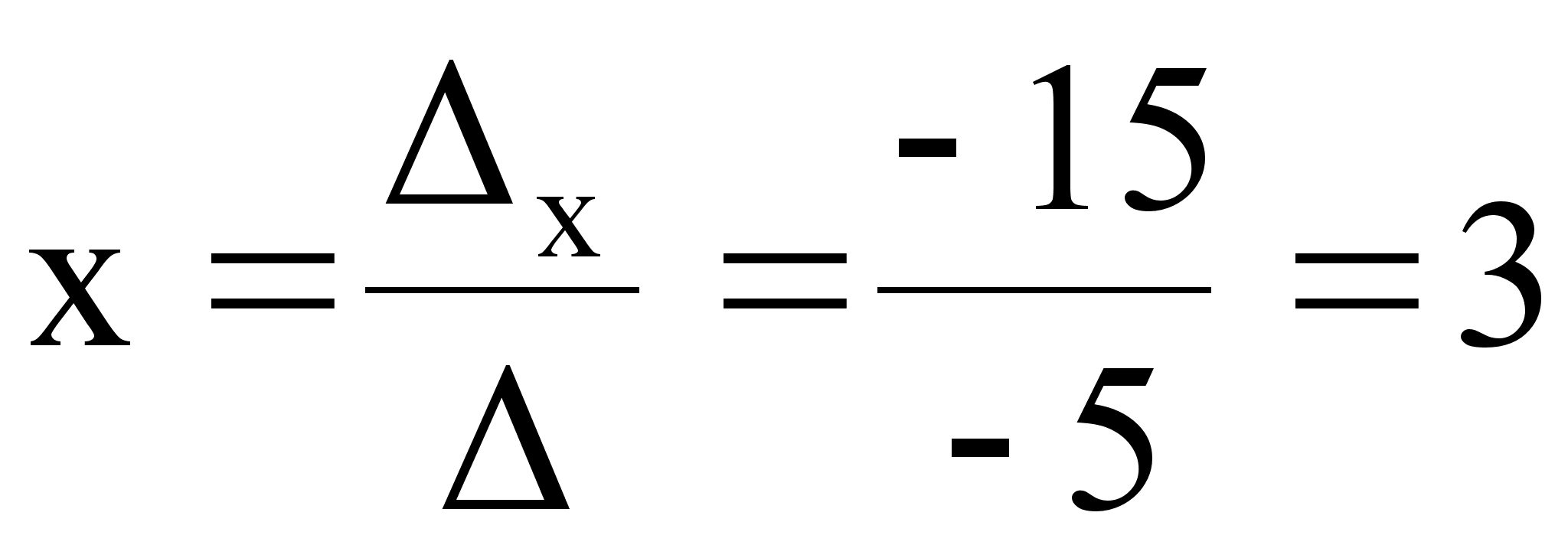



0 комментариев