Определите «на глаз» вид каждого из треугольников, изображенных на слайдах (рис. 7)

8. Определите «на глаз» вид каждого из треугольников, изображенных на слайдах (рис. 7).

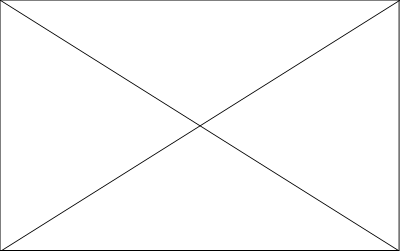
Рис. 7

III. Ученики, работающие по карточкам, сдают выполненное задание. Те, кто работал у доски, рассказывают, как выполняли задание. Дополнительные вопросы им задают ученики.

IV. Итак, на предыдущем уроке мы познакомились с треугольником и изучили их виды.

·  Как же построить равнобедренный треугольник с помощью циркуля и линейки?

·  Ученики предлагают провести произвольный отрезок, затем из концов отрезка как из центров, не меняя раствора циркуля, провести дуги до пересечения. Точку пересечения соединить с концами отрезка.

·  Почему вы уверены, что получился равнобедренный треугольник?

(Взяли раствор циркуля, не равный построенному отрезку и провели дуги равных окружностей. Точка их пересечения находится на равном расстоянии от концов отрезка.)

Вводится название сторон: основание, боковые стороны (рис. 8).

D ABC: AB = BC, ÐA = ÐC.

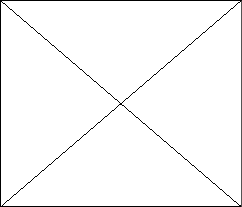
Рис. 8

Измерьте углы при вершинах A и C.

Большинство учеников получают равные градусные меры, и учитель сообщает, что именно таким образом в Древней Греции практическим путем установили, что «углы при основании» равны. И лишь много лет спустя это было доказано.

V. Физкультурная пауза

(Ученики повторяют за учителем все движения.)

VI. Продолжаем работу.

Соедините вершину B с серединой противоположной стороны. Измерьте углы BMC и BMA. Что вы получили?

Ученики делают вывод: ÐBMC = ÐBMA = 90° и дополняют рисунок. Используя модель равнобедренного треугольника, учитель перегибает модель по отрезку BM. Ученики замечают, что треугольники ABM и BMC при наложении совпали, и делают вывод: D ABM = D BMC.

VII. Задание на дом

1. Постройте равнобедренный треугольник.
2. Измерьте все его углы. Сделайте вывод.
3. Проведите отрезки, соединяющие вершины с серединами противоположных сторон. Что вы заметили?

УРОК 3

Тема урока: «Построение треугольников. Равенство треугольников»

Цели урока:

научить учеников строить треугольник, равный данному, используя циркуль и линейку; из опыта практической деятельности учащиеся должны понять, что треугольники равны по трем элементам; каждая сторона треугольника меньше суммы двух других.

Оборудование: у каждого ученика набор чертежных инструментов, цветная бумага, ножницы.

Ход урока

I. Работа с классом

На доске изображены фигуры.

Задания

1. На рисунке 9 проведите прямую так, чтобы она разбила четырехугольник на два треугольника. Определите «на глаз» вид получившихся треугольников.

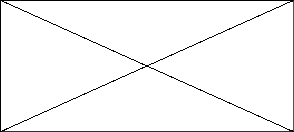
Рис. 9

2. Проведите прямую так, чтобы она разбила четырехугольник (рис. 10) на треугольник и четырехугольник, а на рисунке 11 – на треугольник и пятиугольник.

Рис. 10

Рис. 11

3. Проволоку длиной 15 см согнули так, что получился разносторонний треугольник. Чему равен периметр этого треугольника?

4. Основание равнобедренного треугольника равно 4 см, а боковые стороны вдвое больше основания. Найдите периметр треугольника.

5. В равнобедренном треугольнике один из углов равен 64°. Найдите два других угла этого треугольника.

II. Работа в группах из четырех человек

(Задание для каждой группы с разными данными.)

Постройте треугольник ABC, если:

1) AB = 5 см, AC = 8 см, Р BAC = 50°;
2) CA = 4 см, CB = 6 см, Р ABC = 120°;
3) AB = 7 см, Р CAB = 60°, Р CBA = 30°;
4) OP = 4 см, Р KOP = 20°, Р OPK = 70°;
5) KL = 4 см, LM = 3 см, MK = 2,5 см;
6) AB = 3 см, BC = 4 см, AC = 5 см.

Три группы из шести групп рассказывают, как проводили построение.

Вырежьте получившийся треугольник. Сравните его с треугольниками, построенными учениками из своей группы.

В каждой группе получили равные треугольники. Казалось бы, ничего удивительного нет, данные были одинаковы, но ...

III. Общее задание

·  Постройте треугольник, в котором РA = 30°, РB = 60°, РC = 90°.

·  Что вы замечаете? Какой вывод можно сделать? (У всех разные треугольники.)

IV. Работа в группах

(Задание одинаково для пар групп.)

Постройте треугольники, у которых стороны равны:

1) 6 см, 2 см, 3 см;
2) 6 см, 2 см, 4 см;
3) 6 см, 2 см, 7 см.

В ходе построений и рассуждений ученики приходят к выводу, что у треугольника каждая сторона меньше суммы двух других сторон, в противном случае треугольник построить невозможно.

V. Минутка отдыха

Передайте свое настроение с помощью изображения треугольника.

Кто-то раскрашивает треугольник в разные цвета, кто-то составляет фигурки из треугольников, кто-то изображает рожицы, проявляя выдумку и фантазию (рис. 12, 13).

Рис. 12

Рис. 13

VI. Проверочная работа

Вариант 1

1. Постройте равнобедренный тупоугольный треугольник.
2. В треугольнике DCE ÐD = 24°, ÐC = 58°. Найдите ÐE.
3. Основание равнобедренного треугольника равно 6 см, а боковые стороны в три раза больше. Найдите периметр треугольника.