Навигация
Циркуляция вектора вдоль линии
5. Циркуляция вектора вдоль линии
Роток векторного поля
Элементарная циркуляция вектора ![]() вдоль линии dl равна (рис. 8а)
вдоль линии dl равна (рис. 8а)
![]() (16)
(16)
Циркуляция вектора ![]() вдоль замкнутой линии L (рис. 8б)
вдоль замкнутой линии L (рис. 8б)
![]() (17)
(17)
Пусть контур L ограничивает некоторую поверхность S (рис. 8в). Используем теорему Стокса и преобразуем интеграл по кривой L в интеграл по поверхности S:
![]() (18)
(18)
Роток (вихрь) вектора ![]() определяется как
определяется как
 (19)
(19)
Определение
Циркуляция вектора ![]() вдоль замкнутого контура равна потоку его ротора через поверхность, ограниченную этим контуром (рис. 9)
вдоль замкнутого контура равна потоку его ротора через поверхность, ограниченную этим контуром (рис. 9)
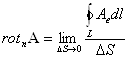 (20)
(20)
Потенциальное векторное поле
Определение:
Векторное поле ![]() называется потенциальным, если существует скалярная величина
называется потенциальным, если существует скалярная величина ![]() , такая, что
, такая, что
![]()
![]() – называется скалярным потенциалом поля.
– называется скалярным потенциалом поля.
Свойства потенциального поля
1. В потенциальном поле отсутствуют вихри (отсутствует ротация), т.е.
![]()
Доказательство:
![]()
2. Циркуляция по любому замкнутому контуру равна нулю (это следствие п.1)
![]()
3. Работа потенциального поля при перемещении точки из одного положения в другое не зависит от пути соединяющего эти положения и равна разности потенциалов в конечных точках.
Циркуляция потенциального поля не зависит от вида кривой, соединяющей две различные точки, и равна разности значений потенциала в данных точках.
![]()
отсюда получаем
![]()
![]()
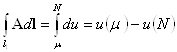
4. Векторные линии потенциального поля не могут быть замкнутыми.
Доказательство от противоположного:
Допустим, что есть замкнутая векторная линия L. Тогда по определению векторной линии вдоль соответствующего контура ![]() и, следовательно, и циркуляция по нему больше нуля
и, следовательно, и циркуляция по нему больше нуля ![]() , что противоречит свойству 2.
, что противоречит свойству 2.
5. Сумма потенциальных векторных полей является потенциальным полем, и потенциал суммы полей равен сумме потенциалов.
Соленоидальное векторное полеОпределение:
Векторное поле![]() называется соленоидальным (вихревым), если существует векторная величина
называется соленоидальным (вихревым), если существует векторная величина ![]() такая, что
такая, что
![]() = rot
= rot ![]()
![]() – называется векторным потенциалом поля
– называется векторным потенциалом поля ![]() .
.
1. Для того чтобы поле ![]() было соленоидальным, необходимо и достаточно, чтобы во всей рассматриваемой области выполнялось равенство div
было соленоидальным, необходимо и достаточно, чтобы во всей рассматриваемой области выполнялось равенство div ![]() = 0, т.е. его поток через всякую замкнутую поверхность, погруженную в поле, = 0. Следовательно, соленоидальные поля лишены источников и стоков.
= 0, т.е. его поток через всякую замкнутую поверхность, погруженную в поле, = 0. Следовательно, соленоидальные поля лишены источников и стоков.
Замечание: Это свойство можно положить в определение.
Доказательство основывается на том, что
![]() =
=
Следствие ![]() = 0
= 0
![]()
как следствие этого свойства получаем, что поток вектора ![]() соленоидального поля через две одинаково ориентированные поверхности S1 и S2, опирающиеся на один и тот же контур L, одинаков.
соленоидального поля через две одинаково ориентированные поверхности S1 и S2, опирающиеся на один и тот же контур L, одинаков.
Похожие работы
... W(x,t+) U X UЕ=Ux/cos т.е. т.к. cos<1,. то фазовая скорость может превышать скорости света Элементы векторного анализа Необходимо уметь анализировать не только скалярные, но и векторные функции точки.Скалярные функции: температура неравномерно нагретого тела, плотность неоднородного тела и т. д.Векторные функции: ...
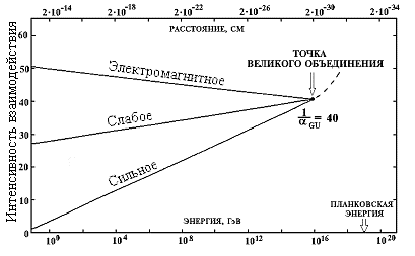
... представляют собой проявление одного и того же фундаментального принципа. Эйнштейн опередил свое время. В то время, когда он жил, еще не было известно сильное и слабое взаимодействие, поэтому он так и не смог выстроить Единую Теорию Поля. Больше того, его поиски в то время были мало понятны большинству физиков - почти все из них были озабочены разработкой новой дисциплины - квантовой механикой. ...
... обстоит несколько сложней, по вполне разрешимо технически и теоретически, что и будет представленно в общих чертах. Теория гравитации (популярное изложение) Известно, миниральное тело – многосложно, а савокупность всевозможных циркуляций и волн среды является его собственным потенциальным полем, что обеспечивает неразрывную, неотемлемую всегда существующую взаимосвязь всего и Универсума в ...
... гештальтпсихологов в связи с решением проблемы целостности психики и анализа психических феноменов с позиции распределения сил, динамики, направления движения. Несмотря на некоторые общие идеи с гештальтпсихологами, теорию поля Курта Левина следует отличать от этого направления. Главной категорией гештальпсихологов был образ, а для Левина таким понятием стал мотив. Теория К. Левина так же как ...

0 комментариев