Навигация
Поток соленоидального поля через два любых сечения векторной трубки одинаков
2. Поток соленоидального поля через два любых сечения векторной трубки одинаков.
Доказательство:
Отрезок векторной трубки, ограниченный сечениями S1, S2 и Sd, можно рассматривать как замкнутую поверхность, помещенную в соленоидальное поле. Поэтому ![]()
![]() , но
, но ![]() , т.к.
, т.к. ![]() .
.
Учитывая, что ![]() и
и ![]() направлены в противоположные стороны, и вводя (–
направлены в противоположные стороны, и вводя (–![]() ), получим
), получим
![]() отсюда следует
отсюда следует ![]()
3. В соленоидальном поле векторные линии либо замкнуты, либо уходят к границе поля. Так как ![]() , то векторные линии поля
, то векторные линии поля ![]() не могут начинаться или кончаться в области поля, иначе в…? будет существовать сток или исток, что противоречит свойству 1.
не могут начинаться или кончаться в области поля, иначе в…? будет существовать сток или исток, что противоречит свойству 1.
4. Сумма соленоидальных векторных полей есть соленоидальное поле.
Потенциальное несжимаемое поле. Гармоническое поле![]() ,
, ![]() отсюда следует
отсюда следует ![]() =
=![]()
![]()
![]()
Это поле часто называют гармоническим или полем Лапласа.
Резюме
По заданному полю ![]() мы всегда можем найти поля u и
мы всегда можем найти поля u и ![]() . Справедливо и обратное утверждение: по известным u и
. Справедливо и обратное утверждение: по известным u и ![]() всегда можно найти искомое поле
всегда можно найти искомое поле ![]() .
.
Пусть поле ![]() известно, тогда потенциалы u и
известно, тогда потенциалы u и ![]() находятся из уравнений:
находятся из уравнений:
![]()
![]()
Если u и ![]() известны, тогда векторное поле
известны, тогда векторное поле ![]() определяется из уравнений:
определяется из уравнений:
![]()
Эти уравнения всегда разрешимы.
Теорема о разложимости произвольного векторного поляПроизвольное векторное поле ![]() всегда может быть представлено в виде суммы потенциального
всегда может быть представлено в виде суммы потенциального ![]() и соленоидального
и соленоидального ![]() полей.
полей.
Задано
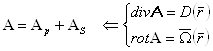
где ![]() ;
; ![]()

и, следовательно ![]()
Потенциалы ![]() и u должны удовлетворять следующему соотношению:
и u должны удовлетворять следующему соотношению:
1. ![]()
но дивергенция соленоидального поля должна быть равна 0.
![]()
отсюда
![]()
![]()
2. ![]()
![]() (**)
(**)
Для определения ![]() и u получили два дифференциальных уравнения, которые всегда имеют решения и, следовательно, произвольное поле
и u получили два дифференциальных уравнения, которые всегда имеют решения и, следовательно, произвольное поле ![]() всегда можно представить в виде суммы потенциального и соленоидального полей.
всегда можно представить в виде суммы потенциального и соленоидального полей.
Для нахождения ![]() и u нужно решить систему четырех уравнений
и u нужно решить систему четырех уравнений
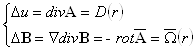
Пусть известны характеристики векторного поля ![]()
![]() (1)
(1)
или в интегральной форме:

Будем искать распределение поля ![]() . Для этого разложим его на потенциальное
. Для этого разложим его на потенциальное ![]() и вихревое
и вихревое ![]() .
.
![]() =
= ![]() +
+ ![]() (2)
(2)
Подставляя (2) в уравнение (1), получим систему уравнений для отыскания ![]() :
:
 (3)
(3)
Потенциальное поле удобно представить через градиент
![]() (4)
(4)
т.к. в этом случае приходится находить всего лишь одну скалярную величину вместо трех. Подставляем (4) в первое уравнение (3), получаем уравнение
![]() – уравнение Пуассона (5)
– уравнение Пуассона (5)
Его решение известно и имеет следующий вид:
![]() . (6)
. (6)
Соленоидальное (вихревое) поле будем искать через векторный потенциал
![]() (7)
(7)
Тогда для ![]() получаем следующее уравнение:
получаем следующее уравнение:
![]() (8)
(8)
Т.к. поле ![]() тоже векторное, то для его нахождения кроме rot необходимо задать еще одно условие на div
тоже векторное, то для его нахождения кроме rot необходимо задать еще одно условие на div ![]() . В качестве такого условия (которое заранее ниоткуда не вытекает) удобно выбрать div
. В качестве такого условия (которое заранее ниоткуда не вытекает) удобно выбрать div![]() = 0 (это называется калибровкой Кирхгофа). В этом случае уравнение (8) упрощается
= 0 (это называется калибровкой Кирхгофа). В этом случае уравнение (8) упрощается
![]() (8а)
(8а)
и его решение имеет вид:
![]() (9)
(9)
Следовательно, искомое поле ![]() равно:
равно:

Интегральные соотношения теории векторного поля
1. Теорема Остроградского-Гаусса
![]()
2. Теорема Стокса
![]()
3. Теорема Грина
(первая форма)
![]()
(вторая форма)
![]()
Похожие работы
... W(x,t+) U X UЕ=Ux/cos т.е. т.к. cos<1,. то фазовая скорость может превышать скорости света Элементы векторного анализа Необходимо уметь анализировать не только скалярные, но и векторные функции точки.Скалярные функции: температура неравномерно нагретого тела, плотность неоднородного тела и т. д.Векторные функции: ...
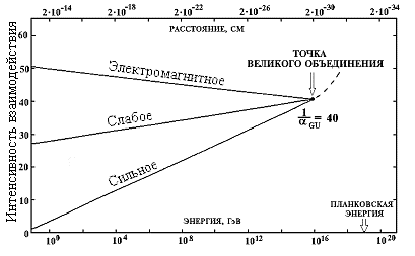
... представляют собой проявление одного и того же фундаментального принципа. Эйнштейн опередил свое время. В то время, когда он жил, еще не было известно сильное и слабое взаимодействие, поэтому он так и не смог выстроить Единую Теорию Поля. Больше того, его поиски в то время были мало понятны большинству физиков - почти все из них были озабочены разработкой новой дисциплины - квантовой механикой. ...
... обстоит несколько сложней, по вполне разрешимо технически и теоретически, что и будет представленно в общих чертах. Теория гравитации (популярное изложение) Известно, миниральное тело – многосложно, а савокупность всевозможных циркуляций и волн среды является его собственным потенциальным полем, что обеспечивает неразрывную, неотемлемую всегда существующую взаимосвязь всего и Универсума в ...
... гештальтпсихологов в связи с решением проблемы целостности психики и анализа психических феноменов с позиции распределения сил, динамики, направления движения. Несмотря на некоторые общие идеи с гештальтпсихологами, теорию поля Курта Левина следует отличать от этого направления. Главной категорией гештальпсихологов был образ, а для Левина таким понятием стал мотив. Теория К. Левина так же как ...

0 комментариев