Навигация
1.2 Уравнения равновесия
Первая группа уравнений выражает условия равновесия элемента среды во взаимодействии с соседними элементами, их называют статическими уравнениями.
Вторая группа уравнений связывает деформации элемента тела с функциями, выражающими перемещение его точек. Они называются геометрическими уравнениями.
Последняя группа уравнений – это уравнения, которые выражают зависимость между напряжениями и деформациями элемента. Именно в этих уравнениях учитываются механические свойства материала, их называют физическими.
Рассмотрим указанные уравнения подробно.
Уравнения равновесия (статические уравнения)
Эти уравнения выражают равенство нулю сумм проекций всех элементарных сил, действующих на элемент ![]() ,
, ![]() , 1 (рис. 1.2). Приняв напряжения, указанные на этом рисунке, за положительные, получим уравнения равновесия в виде
, 1 (рис. 1.2). Приняв напряжения, указанные на этом рисунке, за положительные, получим уравнения равновесия в виде

В этих равенствах учтены проекции сил, действующих на гранях ![]() , которые они дают вследствие наклона на малые углы
, которые они дают вследствие наклона на малые углы ![]() . Косинусы этих малых углов приняты равными единице. Заменив в приведенных равенствах
. Косинусы этих малых углов приняты равными единице. Заменив в приведенных равенствах
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
учтя выражение для частных дифференциалов напряжений (нижние индексы у обозначения частных дифференциалов здесь опущены в целях упрощения записи)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
а также сохранив и отбросив слагаемые высшего порядка малости, получим уравнение равновесия в полярных координатах:

Приравняв нулю сумму моментов сил, действующих на момент ![]() ,
, ![]() , 1, относительно оси, проходящей через его центр перпендикулярно плоскости площадки
, 1, относительно оси, проходящей через его центр перпендикулярно плоскости площадки ![]() ,
, ![]() , и, отбросив слагаемые высшего порядка малости, получим закон парности касательных напряжений
, и, отбросив слагаемые высшего порядка малости, получим закон парности касательных напряжений ![]() .
.
1.3 Формулы Коши (геометрические уравнения)
Эти уравнения устанавливают зависимость между перемещениями и деформациями. Для их вывода будем считать функции ![]() ,
, ![]() заданными, а через них выразим деформации.
заданными, а через них выразим деформации.
Геометрически деформация тела может быть представлена двумя группами простейших деформаций: деформацией растяжения - ![]() ,
, ![]() и деформацией сдвига
и деформацией сдвига ![]() , которые соответственно выражают относительные удлинения отрезков
, которые соответственно выражают относительные удлинения отрезков ![]() и
и ![]() :
:
![]() ,
, ![]() (рис. 1.3)
(рис. 1.3)
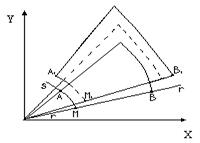
и изменение прямого угла между ними на угол сдвига ![]() :
:
![]() (рис. 1.4)
(рис. 1.4)
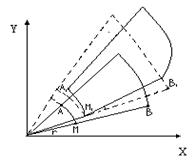
Будем считать, что элемент тела сначала получил перемещение из точки ![]() в точку
в точку ![]() , как жесткое целое, а затем произошел сдвиг за счет поворота его граней на малые углы
, как жесткое целое, а затем произошел сдвиг за счет поворота его граней на малые углы ![]() ,
, ![]() , т.е. угол сдвига равен
, т.е. угол сдвига равен ![]() .
.
Для определения деформации ![]() рассмотрим отрезок
рассмотрим отрезок ![]() длиной
длиной ![]() . Для малых перемещений и деформаций примем, что на изменение длины отрезка влияет лишь перемещение
. Для малых перемещений и деформаций примем, что на изменение длины отрезка влияет лишь перемещение ![]() , а его малый наклон, в общем случае вызываемый перемещением
, а его малый наклон, в общем случае вызываемый перемещением ![]() , не изменяет его длины.
, не изменяет его длины.
Обозначим: ![]() - частный дифференциал (линейная часть приращения) функции и при изменении координаты
- частный дифференциал (линейная часть приращения) функции и при изменении координаты ![]() на
на ![]() .
.
![]() , т.е.
, т.е. ![]()
Тогда
![]() .
.
Аналогично
![]() ,
,
где производная по s заменена на производную по ![]() по соотношению
по соотношению ![]()
![]() , так как
, так как ![]() .
.
Для определения деформации ![]() рассмотрим рис. 1.4. Так как частные дифференциалы
рассмотрим рис. 1.4. Так как частные дифференциалы 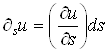 и
и 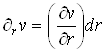 , то
, то
![]() ,
, ![]() .
.
Имеем угол сдвига
![]() , где
, где ![]() .
.
Деформации ![]() ,
, ![]() составляют только часть полных деформаций и поэтому отмечены звездочкой. Другую часть этих деформаций получим, давая точкам элемента перемещения
составляют только часть полных деформаций и поэтому отмечены звездочкой. Другую часть этих деформаций получим, давая точкам элемента перемещения ![]() (рис. 1.5) и
(рис. 1.5) и ![]() (рис. 1.6).
(рис. 1.6).

Соответственно получим деформации, обусловленные кривизной элемента
![]()
![]() ,
,
где знак минус соответствует возрастанию первоначально прямого угла элемента.
Окончательные суммарные деформации
![]() ,
, ![]() ,
, ![]()
будут

Эти равенства представляют геометрические уравнения в полярных координатах, являющиеся аналогом уравнений Коши.
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
... ; 14 – взрывная камера; 15 – затвор; 16 – штамповая оснастка; 17 – штоки; 18 – букса; А – коническое гнездо; В – гидравлическая полость. РАЗРАБОТКА ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ВЗРЫВНОГО ФОРМООБРАЗОВАНИЯ ТРУБЧАТЫХ ДЕТАЛЕЙ Предлагаемые техпроцессы предусматривают возможность проведения операции калибровки, зиговки, конусной и сферической развальцовки трубопроводов диаметрами 8÷60 мм на ...
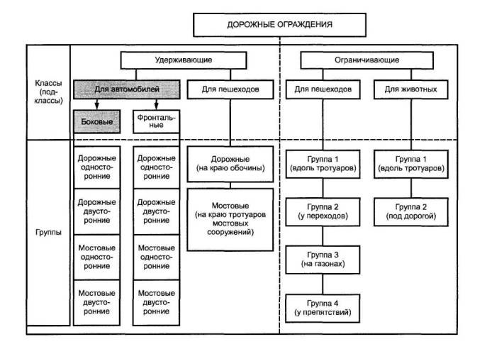
... по техническому регулированию и метрологии от 11 декабря 2006 г. № 296-ст. ГОСТ Р52606-2006 устанавливает классификационные признаки для разделения конструкций дорожных ограждений на классы, группы, типы и виды и предназначается для использования при разработке нормативных и методических документов в области безопасности дорожного движения с целью обеспечения единого понимания определений, ...
... длине и сечению деталей, выдержки и охлаждения. Экспериментальные данные показывают, что при температуре отпуска 650-680 °С пластичность стали полностью восстанавливается через 2-3 часа. После сварки цилиндра гидропресса, он подвергается высокому отпуску в нем при температуре 650±20 °С, для снятия остаточных напряжений. Перед посадкой в печь на отпуск не допускается ее охлаждение ниже 300 °С. ...




0 комментариев