Навигация
2.3 Решение задачи
Осесимметричное (невозмущенное) состояние
Пластичность
Определим компоненты напряжений в пластичной области ![]() .
.
Так как материал трубы считается несжимаемым, то имеет место условие несжимаемости:
![]() . (2.3.1)
. (2.3.1)
Труба осесимметрическая, следовательно компоненты и напряжения, и перемещения от ![]() не зависят:
не зависят:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Условие пластичности (2.2.19) в начальном состоянии имеет вид:
![]() . (2.3.2)
. (2.3.2)
Из условий равновесий (2.2.17) вытекает:
 .
.
Получили дифференциальное уравнение:
 .
.
Решим:

Из граничных условий (2.2.21) имеем
![]() .
.
Тогда
 (2.3.3)
(2.3.3)
Определим компоненты перемещений.
Из формул Коши (2.2.18) следует:
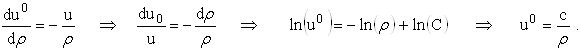
При ![]() из граничных условий (2.2.21) следует
из граничных условий (2.2.21) следует
![]()
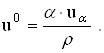
Упругость
Найдем компоненты деформации в упругой области ![]() .
.
Из закона Гука (2.2.20) вытекает
![]() (2.3.4)
(2.3.4)
Формулы Коши (2.2.18) примут вид:

Из уравнений равновесий (2.2.17):
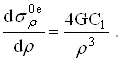
Решим:
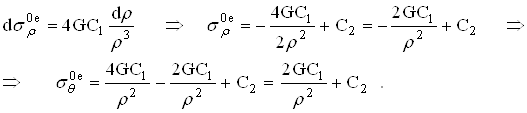
Из граничных условий (2.2.21) ![]() при
при
![]()

Тогда
 (2.3.5)
(2.3.5)
При ![]() и
и ![]()
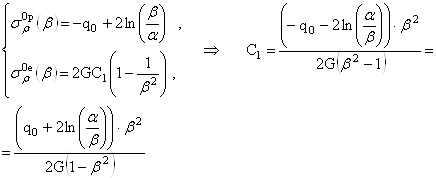
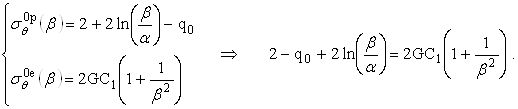 (2.3.6)
(2.3.6)
Получили неявное уравнение для нахождения радиуса пластической зоны ![]() .
.
![]() Возмущенное состояние
Возмущенное состояние
Пластичность
Решение будем искать в виде:
 где
где ![]() (2.3.7)
(2.3.7)
Из условия пластичности (2.3.7) следует:
![]() .
.
![]() .
.
![]()
![]()
![]()
![]() .
.
Формулы (2.2.23) примут вид:
 (2.3.8)
(2.3.8)
Из условия пластичности (2.2.19) и формул (2.3.8) получим:
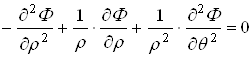 .
.![]()
Функцию ![]() будем искать в виде:
будем искать в виде:
![]() .
.
Подставим
![]()

Пусть

Тогда

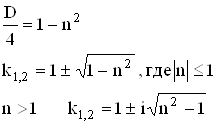
Следовательно
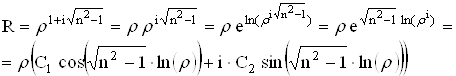
Или
![]() .
.
Тогда функция ![]() примет вид:
примет вид:
![]() . (2.3.9)
. (2.3.9)
Найдем частные производные по ![]() и по
и по ![]() .
.
![]()
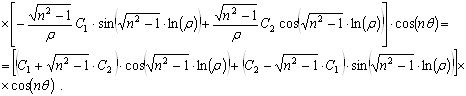
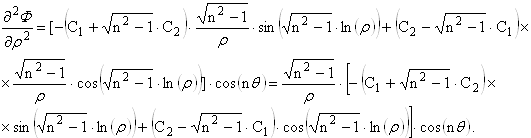

По формулам (2.3.8) при подстановке имеем:
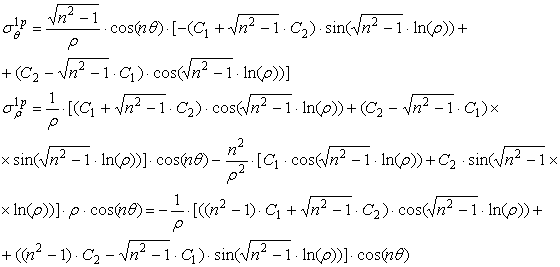
![]()

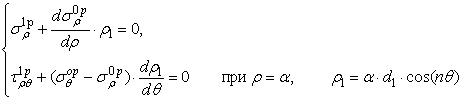
Из этих соотношений найдём ![]()

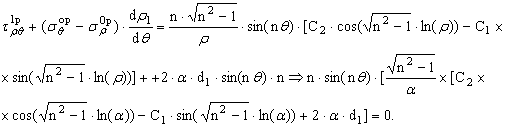
Составим систему уравнений и решим её.
Введём обозначения: ![]()
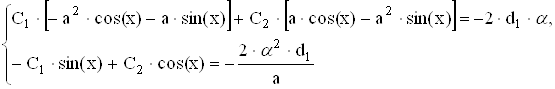
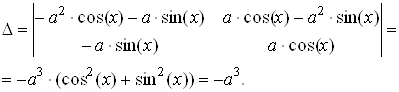

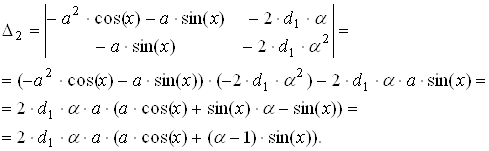
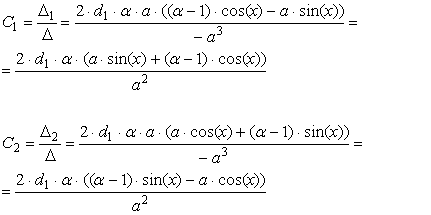 (2.3.11)
(2.3.11)
Упругость
Закон Гука:
 (2.3.12)
(2.3.12)
Формулы Коши:
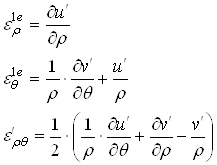 (2.3.13)
(2.3.13)
Уравнения равновесия:
 (2.3.14)
(2.3.14)
Условие несжимаемости:
![]() (2.3.15)
(2.3.15)
Закон Гука можно переписать в виде:

![]()
Сложим уравнения системы:
 (2.3.12)
(2.3.12)
можно записать так:
 (2.3.16)
(2.3.16)
Условие несжимаемости (2.3.15) в силу (2.3.13) примет вид:

Положим
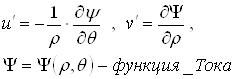
Тогда (2.3.16) запишется в виде:
 (2.3.17)
(2.3.17)
Подставим (2.3.17) в (2.3.14):
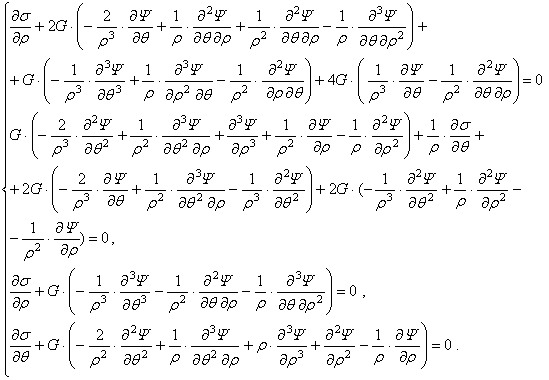
Первое выражение продифференцируем по![]() , второе - по
, второе - по ![]() , вычтем из первого выражения второе и разделим на
, вычтем из первого выражения второе и разделим на ![]() . Тогда
. Тогда
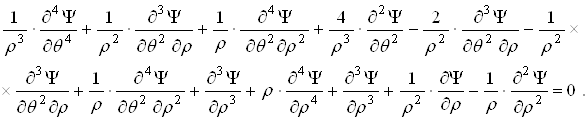
![]() Умножим на
Умножим на ![]() .
.
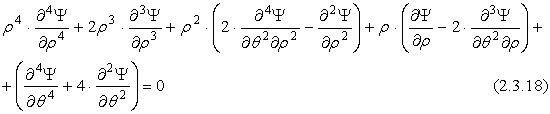
Функцию ![]() будем искать в виде:
будем искать в виде:
![]()
Подставим в (2.3.18) и разделим на ![]() .
.

Решение будем искать в виде ![]() .
.
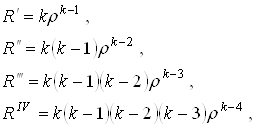
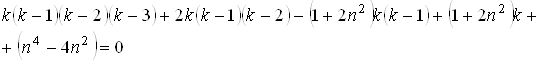
Или

Тогда
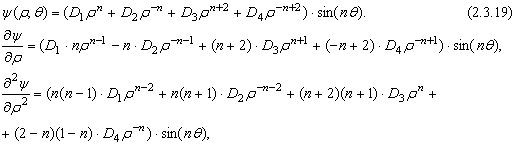
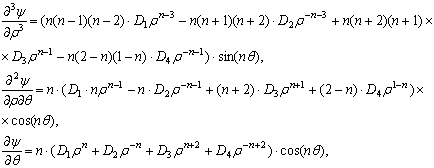

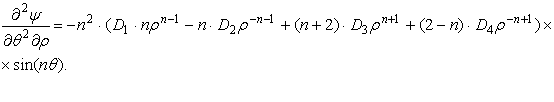

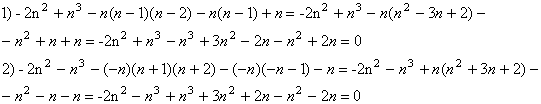

Тогда компоненты напряжений имеют вид:
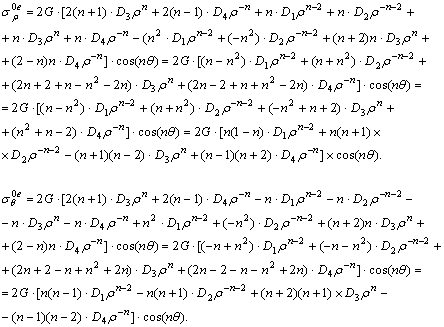

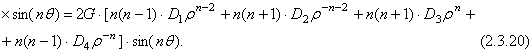
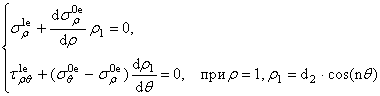
![]()
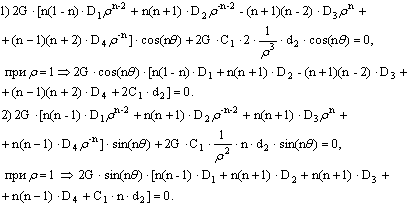
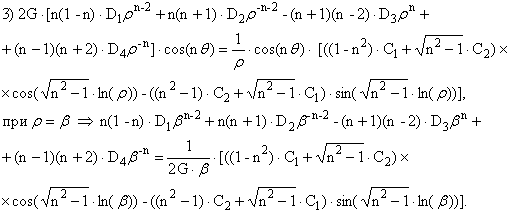
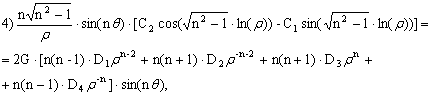

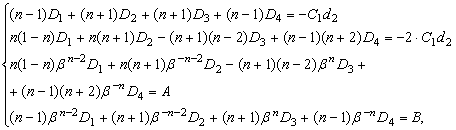
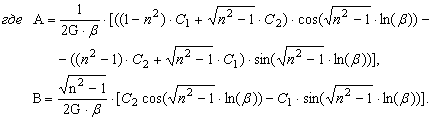
Получили систему уравнений для нахождения коэффициентов ![]() Решим её методом Крамера.
Решим её методом Крамера.
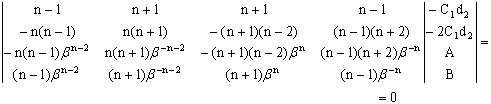


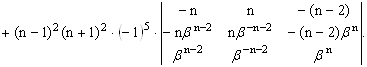

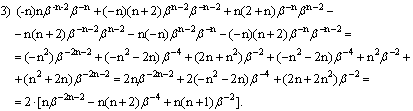
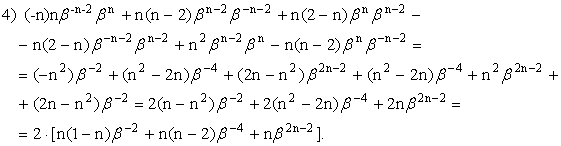
Тогда

![]()
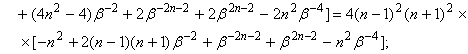


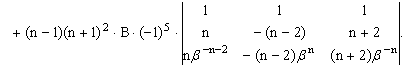

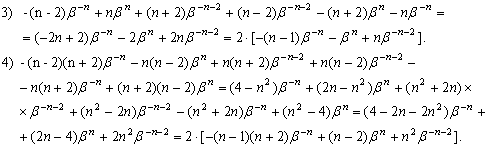
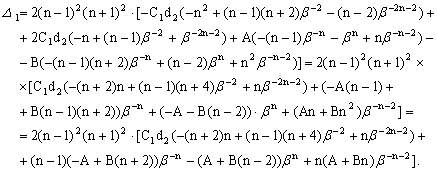
Тогда




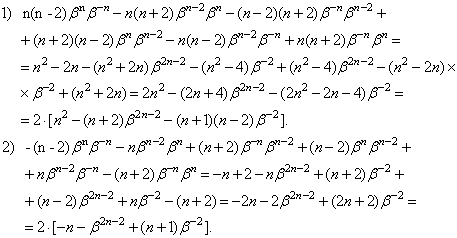

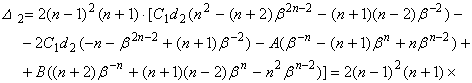
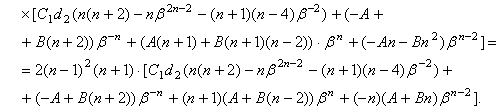
Тогда
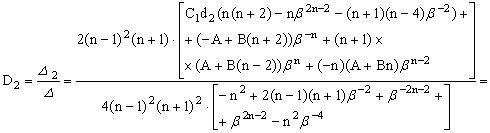
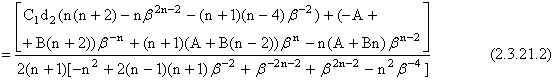




Тогда
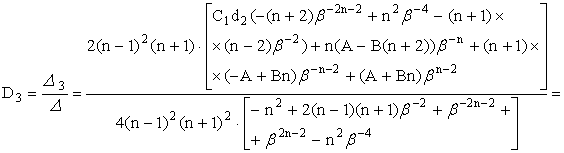

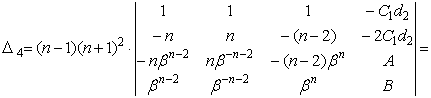

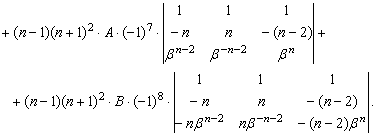
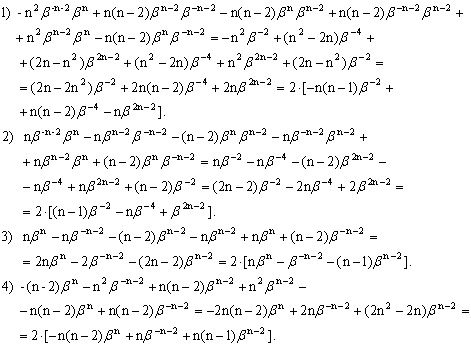
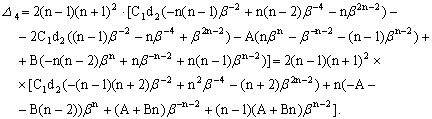
Тогда

Найдём выражения для компонент деформации.
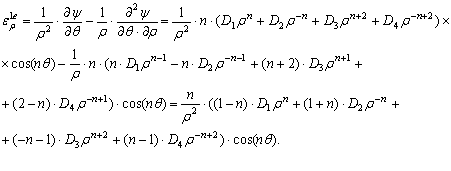

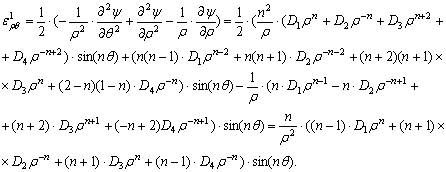
ВЫВОДЫ
Задача решена путём приведения к линеаризованному виду. На первом этапе получено решение осесимметричного (невозмущенного) состояния трубы в напряжениях, деформациях и перемещениях – формулы(2.3.3), (2.3.5), а также неоднородное нелинейное уравнение для нахождения радиуса пластической зоны (2.3.6).
Исследуя осесимметричную деформацию трубы, получено решение задачи в общем случае (n>1). Решение записано в виде (2.3.10), где коэффициенты имеют вид (2.3.11) – это в пластической зоне. В упругой зоне – это формулы (2.3.20), а коэффициенты – (2.3.21).
ЛИТЕРАТУРА
1. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. – М.: Высшая школа, 1990.– 400 с.
2. Бородин Н.А. Сопротивление материалов. – М.: Машиностроение, 1992. – 224 с.
3. Вульман С.А. О решении осесимметричных упругопластических задач методом малого параметра. – Изв. АН СССР, Механика твердого тела, 1969, №3.
4. Ершов Л.В., Ивлев Д.Д. Упругопластическое состояние конической трубы, находящейся под действием внутреннего давления. – Вестник МГУ, 1957, №2.
5. Ершов Л.В., Ивлев Д.Д. Упругопластическое состояние эллиптической трубы, находящейся под действием внутреннего давления. – Изв. АН СССР, 1957, №9.
6. Ивлев Д.Д. Метод возмущений в теории упругопластического тела. – М.:Наука, 1978. – 208 с.
7. Ивлев Д.Д. Приближенное решение упругопластических задач теории идеальной пластичности. – Докл. АН СССР, 1957, т.113, №2.
8. Ивлев Д.Д. Приближенное решение плоских упругопластических задач теории идеальной пластичности. – Вестник МГУ, 1957, №5.
9. Самуль В.И. Основы теории упругости и пластичности. – М.: Высшее образование, 1982. – 264 с.
10. Тимошенко С.П. , Гудгер Дж. Теория упругости. – М.: Наука, 1979. – 560 с.
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
... ; 14 – взрывная камера; 15 – затвор; 16 – штамповая оснастка; 17 – штоки; 18 – букса; А – коническое гнездо; В – гидравлическая полость. РАЗРАБОТКА ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ВЗРЫВНОГО ФОРМООБРАЗОВАНИЯ ТРУБЧАТЫХ ДЕТАЛЕЙ Предлагаемые техпроцессы предусматривают возможность проведения операции калибровки, зиговки, конусной и сферической развальцовки трубопроводов диаметрами 8÷60 мм на ...
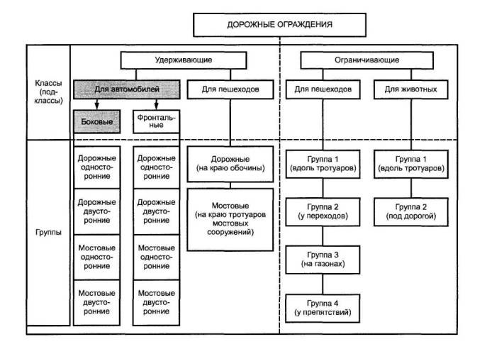
... по техническому регулированию и метрологии от 11 декабря 2006 г. № 296-ст. ГОСТ Р52606-2006 устанавливает классификационные признаки для разделения конструкций дорожных ограждений на классы, группы, типы и виды и предназначается для использования при разработке нормативных и методических документов в области безопасности дорожного движения с целью обеспечения единого понимания определений, ...
... длине и сечению деталей, выдержки и охлаждения. Экспериментальные данные показывают, что при температуре отпуска 650-680 °С пластичность стали полностью восстанавливается через 2-3 часа. После сварки цилиндра гидропресса, он подвергается высокому отпуску в нем при температуре 650±20 °С, для снятия остаточных напряжений. Перед посадкой в печь на отпуск не допускается ее охлаждение ниже 300 °С. ...




0 комментариев