Навигация
Механическая постановка задачи
2.1 Механическая постановка задачи
Рассмотрим упругопластическое состояние трубы радиусов
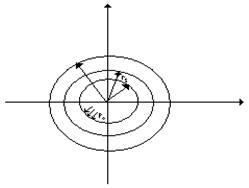
Цель данной задачи – определить выражения для компонент напряжений, скоростей перемещений и скоростей деформации.
Методом решения задачи является метод малого параметра, в качестве которого выбирается величина ![]() , характеризующая возмущения границ трубы.
, характеризующая возмущения границ трубы.
Приведем основные обозначения:
![]() - компоненты напряжений,
- компоненты напряжений,
![]() - компоненты деформаций,
- компоненты деформаций,
![]() - радиальное и тангенциальное перемещения,
- радиальное и тангенциальное перемещения,
![]() - внутренний и внешний радиусы осесимметричной трубы,
- внутренний и внешний радиусы осесимметричной трубы,
![]() - полярный радиус,
- полярный радиус,
![]() - полярный угол,
- полярный угол,
![]() - полярный радиус границы пластической зоны,
- полярный радиус границы пластической зоны,
![]() - модуль сдвига.
- модуль сдвига.
Индекс ![]() указывает на принадлежность компонента к пластической зоне, индекс
указывает на принадлежность компонента к пластической зоне, индекс ![]() - к упругой.
- к упругой.
Все величины, имеющие размерность напряжения, отнесём к величине предела текучести ![]() , величины, имеющие размерность длины, - к внешнему радиусу
, величины, имеющие размерность длины, - к внешнему радиусу ![]() .
.
Обозначим:
![]()
![]() - внешний радиус;
- внешний радиус;
![]()
2.2 Математическая постановка задачи
Предположим, что искомое решение зависит от некоторого параметра ![]() . Будем искать решение в виде рядов по степеням этого параметра
. Будем искать решение в виде рядов по степеням этого параметра
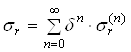 ,
, 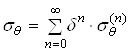 ,
, 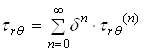 ,
,
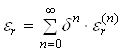 ,
, 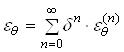 ,
,  ,
,
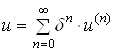 ,
, 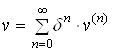 . (2.2.1)
. (2.2.1)
Линеаризация по параметру ![]() заключается в разложении всех исходных соотношений: уравнений равновесия, граничных условий и т.п. в ряды по этому параметру. Далее выделяются члены разложения при одинаковых степенях этого параметра, которые определяют систему уравнений, позволяющую развить метод последовательных приближений, если решение при
заключается в разложении всех исходных соотношений: уравнений равновесия, граничных условий и т.п. в ряды по этому параметру. Далее выделяются члены разложения при одинаковых степенях этого параметра, которые определяют систему уравнений, позволяющую развить метод последовательных приближений, если решение при ![]() является известным.
является известным.
Уравнения равновесия линейны относительно компонент напряжений, поэтому они имеют место для любого приближения. Соотношения связи между компонентами перемещений и деформаций также линейны относительно компонент деформаций и перемещений, поэтому они сохраняют свой вид для любого приближения.
Рассмотрим граничные условия в напряжениях. Ограничимся случаем, когда граничные условия заданы на контуре ![]() в плоскости двух переменных
в плоскости двух переменных ![]() ,
, ![]() . Пусть на границе заданы нормальные и касательные усилия
. Пусть на границе заданы нормальные и касательные усилия
![]() ,
, ![]() на
на ![]() . (2.2.2)
. (2.2.2)
Уравнение границы ![]() представим в виде
представим в виде
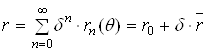 ,
, 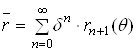 . (2.2.3)
. (2.2.3)
Подставляя в (2.2.2) разложение и учитывая, что для компонент ![]() ,
, ![]() справедливы разложения, аналогичные (2.2.1), получим при
справедливы разложения, аналогичные (2.2.1), получим при ![]() разложение
разложение
 (2.2.4)
(2.2.4)
Ограничиваясь четвертым приближением, из (2.2.4) получим, что при ![]() имеет место
имеет место
 (2.2.5)
(2.2.5)
Совершенно аналогично записываются выражения линеаризованных граничных условий для ![]() : чтобы получить линеаризованные граничные условия для
: чтобы получить линеаризованные граничные условия для ![]() , надо в (2.2.5) заменить
, надо в (2.2.5) заменить ![]() на
на ![]() .
.
В линеаризованных задачах теории пластичности необходимо уметь записывать граничные условия (2.2.2) через компоненты основной системы координат. Для этого следует учесть угол поворота напряжений при переносе их на исходную окружность (![]() ).
).

Рассмотрим рис 1.8. Угол ![]() , образован нормалью к контуру
, образован нормалью к контуру ![]() ;
;
![]() - угол поворота напряжений при переносе их на исходный контур. Из известных формул теории упругости будем иметь
- угол поворота напряжений при переносе их на исходный контур. Из известных формул теории упругости будем иметь
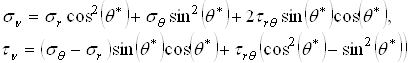 (2.2.6)
(2.2.6)
Если уравнение границы тела ![]() записать в виде
записать в виде ![]() , то
, то
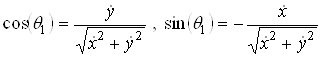 (2.2.7)
(2.2.7)
Согласно (2.2.3) можно записать
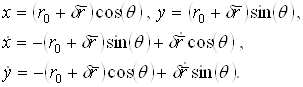 (2.2.8)
(2.2.8)
Учитывая, что
 (2.2.9)
(2.2.9)
Из (2.2.9), (2.2.7), (2.2.8) получим
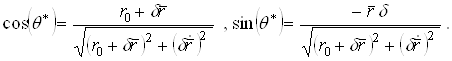 (2.2.10)
(2.2.10)
Обозначая  , найдем
, найдем
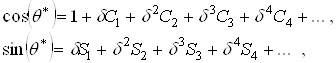 (2.2.11)
(2.2.11)
 (2.2.12)
(2.2.12)
Используя (2.2.1), (2.2.5), (2.2.6), (2.2.11), (2.2.12), получим искомые линеаризованные граничные условия: при ![]() должно иметь место
должно иметь место
 (2.2.13)
(2.2.13)
Перейдем к условиям сопряжения решений. На ![]() - границе упругой и пластической областей, должно иметь место
- границе упругой и пластической областей, должно иметь место
![]() (2.2.14)
(2.2.14)
Уравнение контура ![]() запишется в виде
запишется в виде
![]() (2.2.15)
(2.2.15)
Учитывая разложение (2.2.1), подставляя в (2.2.14) выражение (2.2.15), получим исходное линеаризованное условие сопряжения. Очевидно, что условия сопряжения могут быть получены из (2.2.5), если заключить левые части в квадратные скобки, поменять в них ![]() на
на ![]() , …, а
, …, а ![]() на
на ![]() .
.
Выпишем условия сопряжения для компоненты ![]() :
:
 (2.2.16)
(2.2.16)
Условие сопряжения для компонент ![]() имеют вид, вполне аналогичный (2.2.16).
имеют вид, вполне аналогичный (2.2.16).
Рассмотрим граничные условия в перемещениях:
![]() на
на ![]() .
.
Уравнение границы ![]() представим в виде (2.2.3). Учитывая, что для компонент
представим в виде (2.2.3). Учитывая, что для компонент ![]() справедливы разложения, аналогичные (2.2.3), получим при
справедливы разложения, аналогичные (2.2.3), получим при ![]() разложения, аналогичные (2.2.4), (2.2.5).
разложения, аналогичные (2.2.4), (2.2.5).
Распишем основные соотношения, используемые для решения задачи:
Уравнения равновесия
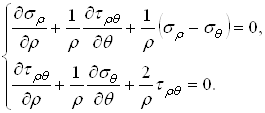 (2.2.17)
(2.2.17)
Формулы Коши
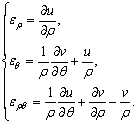 (2.2.18)
(2.2.18)
Условие пластичности
![]() (2.2.19)
(2.2.19)
Закон Гука
 (2.2.20)
(2.2.20)
Граничные условия:
![]() ,
, ![]() ,
,
![]() при
при ![]() ; (2.2.21)
; (2.2.21)
![]() при
при ![]() ;
;
![]() при
при ![]() .
.
Решение будем искать в виде:
 (2.2.22)
(2.2.22)
Уравнения равновесия (2.2.17) удовлетворяются, если ввести некоторую функцию ![]() , называемую функцией напряжений. Это функция
, называемую функцией напряжений. Это функция ![]() связана с компонентами напряжения следующими зависимостями:
связана с компонентами напряжения следующими зависимостями:
 (2.2.23)
(2.2.23)
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
... ; 14 – взрывная камера; 15 – затвор; 16 – штамповая оснастка; 17 – штоки; 18 – букса; А – коническое гнездо; В – гидравлическая полость. РАЗРАБОТКА ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ВЗРЫВНОГО ФОРМООБРАЗОВАНИЯ ТРУБЧАТЫХ ДЕТАЛЕЙ Предлагаемые техпроцессы предусматривают возможность проведения операции калибровки, зиговки, конусной и сферической развальцовки трубопроводов диаметрами 8÷60 мм на ...
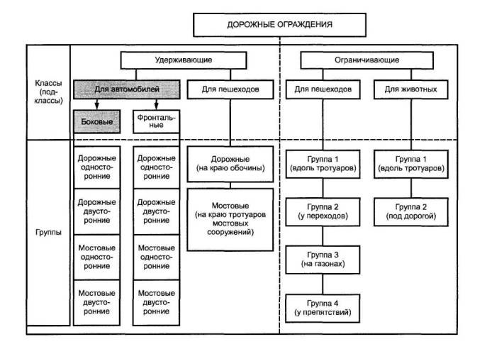
... по техническому регулированию и метрологии от 11 декабря 2006 г. № 296-ст. ГОСТ Р52606-2006 устанавливает классификационные признаки для разделения конструкций дорожных ограждений на классы, группы, типы и виды и предназначается для использования при разработке нормативных и методических документов в области безопасности дорожного движения с целью обеспечения единого понимания определений, ...
... длине и сечению деталей, выдержки и охлаждения. Экспериментальные данные показывают, что при температуре отпуска 650-680 °С пластичность стали полностью восстанавливается через 2-3 часа. После сварки цилиндра гидропресса, он подвергается высокому отпуску в нем при температуре 650±20 °С, для снятия остаточных напряжений. Перед посадкой в печь на отпуск не допускается ее охлаждение ниже 300 °С. ...




0 комментариев