Навигация
Интегральное представление бесселевых функций с целым индексом
16512
знаков
0
таблиц
7
изображений
4. Интегральное представление бесселевых функций с целым индексом
Производящая функция системы функций
Рассмотрим систему 
функций 
(с любой общей областью определения), пронумерованных с помощью всех целых чисел:
Составим ряд
,
где 
– комплексная переменная. Предположим, что при каждом 
(принадлежащем области определения рассматриваемых функций) этот ряд имеет кольцо сходимости, содержащее внутри себя единичную окружность 
. В частности, это кольцо может представлять собой полную плоскость комплексной переменной без точек 0 и ∞.
Функция
(16)
(где x лежит в области определения функций системы , – внутри кольца сходимости, соответствующего рассматриваемому значению ) называется производящей функцией системы .
Обратно, пусть задана функция 
, где пробегает некоторое множество, находится внутри некоторого кольца, зависящего от , с центром 0 и содержащего внутри себя единичную окружность. Тогда, если при каждом аналитична относительно внутри соответствующего кольца, то есть производящая функция некоторой системы функций. В самом деле, разложив при каждом функцию в ряд Лорана по степеням :
,
найдем, что система коэффициентов 
этого ряда будет искомой системой .
Формулы для коэффициентов ряда Лорана позволяют выразить функции рассматриваемой системы через производящую функцию. Применяя эти формулы и преобразовывая затем интеграл вдоль единичной окружности в простой интеграл, получим:
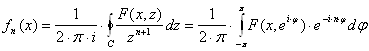. (17)
Производящая функция системы бесселевых функций с целыми индексами
Покажем, что для системы бесселевых функций первого рода с целыми индексами 
(
…) производящая функция есть:
.
Имеем:
, 
,
откуда после почленного перемножения этих равенств найдем:
(так как в предпоследней внутренней сумме 
и 
были связаны зависимостью 
, то мы могли положить 
, получив суммирование по одному индексу ). В последней внутренней сумме суммирование производится по всем целым , для которых 
, следовательно, при 
это будет 
; при 
это будет 
. Таким образом, во всех случаях внутренняя сумма есть в силу формул (5`) и (5```). Итак,
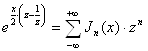, (18)
но это и доказывает, что 
есть производящая функция для системы .
Выведем некоторые следствия из формулы (18). Полагая в ней 
, получим:
,
откуда после разделения действительной и мнимой части (учитывая, что 
)
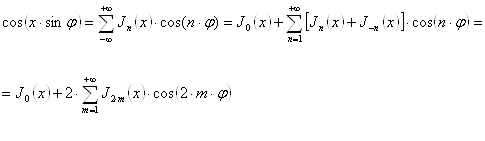(18`)
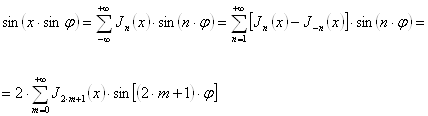(18``)
Заменяя в (18`) и (18``) 
на 
, найдем:
, (18```)
. (18````)
Интегральное представление Jn(x)
Так как, по доказанному, при 
имеем , то по формуле (17) получаем (используя в преобразованиях формулы Эйлера):
где принято во внимание, что 
есть четная функция от 
есть нечетная функция от . Итак, доказано, что для любого целого числа 
. (19)
Формула (19) дает представление бесселевых функций с целым индексом в виде определенного интеграла, зависящего от параметра . Эта формула называется интегральным представлением Бесселя для , правая часть формулы называется интегралом Бесселя. В частности, при 
найдем:
. (19`)
Похожие работы
... К. Лавриновича «Фридрих Вильгельм Бессель, 1784 – 1846: Астроном, геодезист, математик»,[2] а также справочные издания и энциклопедии, в том числе Брокгауза и Евфрона. §1. Начало научной деятельности Бесселя Немецкий астроном и математик Фридрих Вильгельм Бессель родился в небольшом городе Минден на северо-западе Германии в семье мелкого чиновника в 1784 году. С 15 лет должен был встать на ...
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
... В.В. О построении собственных значений и функций одной газодинамической задачи Франкеля // Математическое моделирование. 1990. Т. 2. № 10. С. 100-109. Моисеев Е.И. о решении вырождающихся уравнений с помощью биортогональных рядов // Дифференц. уравнения. 1991. Т. 27. № 1. С. 94-103. Мамедов Я.Н. О некоторых задачах на собственные значения для уравнения смешанного типа // Дифференц. уравнения
... к задаче [6]: найти регулярное в области решение уравнения (1), непрерывное вместе с производной в замкнутой области и удовлетворяющее граничным условиям (4) и . Решение этой задачи задается формулой : где – функция Грина этой задачи для уравнения . (28) Функция Грина выражается через фундаментальные решения уравнения (28), которые имеют вид: где ; ; – функция Бесселя. Функции , ...
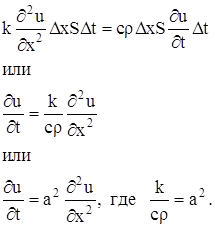
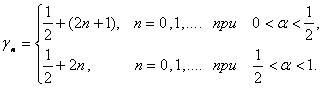
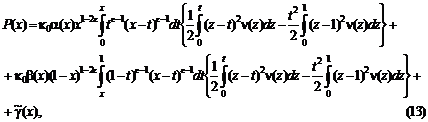
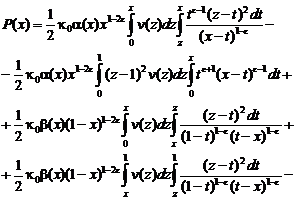
0 комментариев