Навигация
Вычисление верхнего центрального показателя системы
4.2 Вычисление верхнего центрального показателя системы
По-прежнему рассматриваем систему (1):
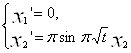 .
.
Применительно к нашей системе семейство кусочно непрерывных и равномерно ограниченных функций P состоит из двух функций ![]() и
и![]() , то есть
, то есть
P![]() ,
,
где
![]()
Для вычисления верхнего центрального показателя ![]() нам понадобится функция
нам понадобится функция
![]() .
.
Докажем, что функция ![]() является верхней для семейства P.
является верхней для семейства P.
Доказательство:
По определению 1.7 ![]() ─ верхняя функция для семейства P, если
─ верхняя функция для семейства P, если
![]() .
.
Докажем, что ![]() .
.
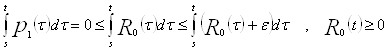 .
.
Следовательно,
![]() .
.
Докажем, что ![]() .
.
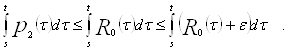
Следовательно,
![]() ,
,
то есть для любого ![]()
![]()
Тогда по определению верхней функции
![]() (P) .
(P) .
Вычислим ![]() .
.
По определению 1.6 верхнего среднего значения функции

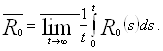
Для всякого ![]() найдется такое
найдется такое ![]() , что
, что
![]() .
.
Тогда
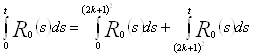 .
.
Вычислим отдельно 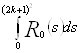 .
.
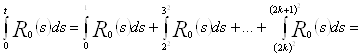
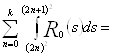
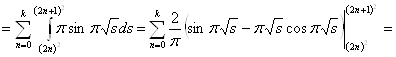
![]()
![]()
Итак,
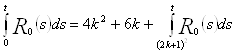 .
.
Оценим сверху 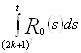 .
.
 . (*)
. (*)
Учитывая (*) и оценивая 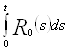 сверху, получаем
сверху, получаем
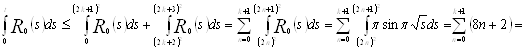
![]() .
.![]()
Тогда (при ![]() )
)
 ,
,
то есть ![]() .
.
Оценивая 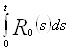 снизу, получаем
снизу, получаем
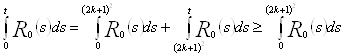 ,
,
где ![]() .
.
Тогда
 ,
,
то есть ![]() .
.
Следовательно, ![]() .
.
Теперь изобразим функции ![]() , и
, и ![]() на графике.
на графике.
График функции ![]() :
:
![]()
![]()
![]()
![]()
![]()
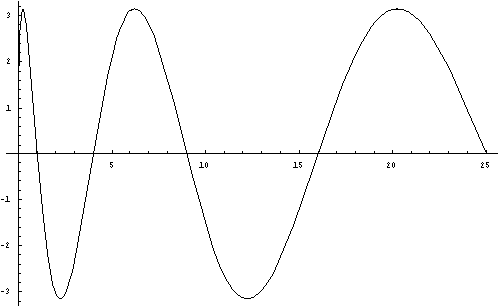
График функции ![]() :
:
![]()
![]()
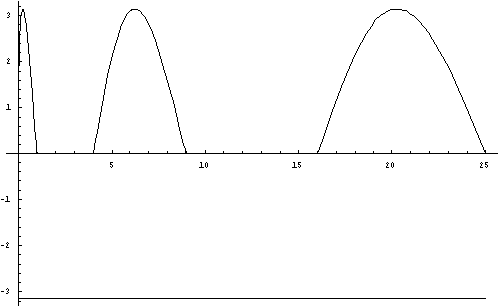
Очевидно, что на отрезках ![]()
![]() ,
,
а на отрезках ![]()
![]() для любого
для любого ![]() .
.
Теперь покажем, что верхний центральный показатель ![]() совпадает с
совпадает с ![]() , то есть
, то есть
![]() .
.
Докажем следующим образом:
1.Введем функцию ![]() .
.
Разобьем ось ![]() на промежутки
на промежутки ![]() точками
точками ![]()
Используя определение 1.12, положим
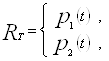 если
если 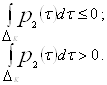
Оценим ![]() .
.
Возможны три случая:
1) если ![]() , то
, то ![]() ; значит,
; значит,
![]() .
.
2) если ![]() , то
, то ![]() ; значит,
; значит,
![]() .
.
2) если ![]() , то
, то ![]() ; значит,
; значит,
![]() .
.
Таким образом, ![]() .
.
2.Докажем, что ![]() .
.
Очевидно, что ![]() ─ функция ограниченная и
─ функция ограниченная и
![]() .
.
Отсюда следует, что
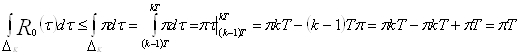 ,
,
то есть
![]() ,
,
Так как
![]() ,
,
то
![]() .
.
3.Докажем, что ![]() для любого
для любого ![]() .
.
По определению 1.6 вычислим ![]() , используя утверждение 1.2:
, используя утверждение 1.2:
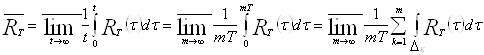 .
.
По определению 1.6 вычислим ![]() , используя утверждение 1.2:
, используя утверждение 1.2:
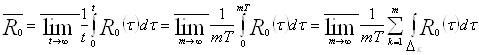 .
.
Теперь рассмотрим все возможные случаи расположений отрезков ![]() по отношению к отрезкам
по отношению к отрезкам ![]() и
и ![]() .
.
I. Если ![]() , где
, где ![]() , то
, то
![]() ,
,
следовательно,
![]() ;
;
II. если ![]() , где
, где ![]() , то
, то
![]() ,
,
следовательно,
![]() ;
;
![]()
III. если ![]() ,
,
то
![]() ;
;
IV. если ![]() ,
,
то
![]() ;
;
1) Для каждого ![]() найдется такое
найдется такое ![]() , что выполняется
, что выполняется
![]() .
.
Тогда
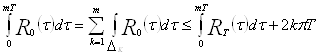 ;
;
2) Для каждого ![]() найдется такое
найдется такое ![]() , что выполняется
, что выполняется
![]() .
.
Тогда
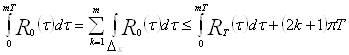 .
.
Из вышеперечисленных случаев 1) и 2) следует, что
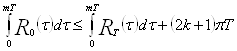 , (**)
, (**)
для любого ![]() такого, что
такого, что
![]() ,
, ![]() .
.
Учитывая неравенство (**), перейдем к непосредственному доказательству неравенства ![]() :
:
![]()
![]() .
.
Теперь оценим выражение ![]() .
.
Очевидно, выполняется следующее неравенство:
![]() .
.
Перейдем к пределам:
![]() ,
,
![]() .
.
Следовательно,
![]() .
.
Значит,
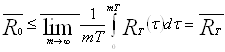 ,
,
то есть для любого ![]()
![]() .
.
По определению 1.11
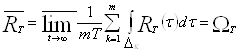 .
.
Таким образом,
![]() для любого
для любого ![]() .
.
По замечанию 1.4 получаем, что
![]() .
.
Следовательно,
![]() .
.
Так как мы доказали, что ![]() (P), то есть
(P), то есть ![]() - верхняя функция для семейства P, то, опираясь на определение 1.9, получаем, что
- верхняя функция для семейства P, то, опираясь на определение 1.9, получаем, что
![]() ,
,
то есть
![]() .
.
А значит,
![]() .
.
Итак, в этом разделе был рассмотрен случай
![]() .
.
5. ОСНОВНЫЕ СВОЙСТВА ВЕРХНЕГО ЦЕНТРАЛЬНОГО ПОКАЗАТЕЛЯ
Р.Э. Виноград ввел[5] понятие верхнего центрального показателя ![]() системы
системы
![]() . (1)
. (1)
Переход от невозмущенной системы (1) к возмущенной системе
![]()
сопровождается изменением показателей. Верхний центральный показатель ![]() системы (1) и характеризует это изменение в определенном классе возмущений. Имеет место теорема Р.Э. Винограда.
системы (1) и характеризует это изменение в определенном классе возмущений. Имеет место теорема Р.Э. Винограда.
Теорема [2,с.164-166;3]. Для любого ![]() можно указать
можно указать ![]() , что при любых непрерывных возмущениях
, что при любых непрерывных возмущениях ![]() ,
,
![]() ,
,
будут выполняться неравенства
![]() .
.
В.В. Миллионщиковым доказано, что последняя оценка неулучшаема, а именно
Теорема [4]. Для любого ![]() найдется возмущение
найдется возмущение
![]() Qe
Qe![]()
![]() , ||Qe
, ||Qe![]() ||
||![]() ,
,
такое, что система
![]() Qe
Qe![]()
имеет решение ![]() , для которой
, для которой
![]() .
.
Значит, для рассмотренной в дипломной работе системы наиболее быстро растущими решениями «руководит» показатель ![]() , а не показатель
, а не показатель ![]() .
.
ЗАКЛЮЧЕНИЕ
В данной дипломной работе рассматриваются соотношения между старшим![]() и верхним центральным
и верхним центральным![]() показателями линейной системы
показателями линейной системы
![]()
с кусочно непрерывными ограниченными коэффициентами.
Показано, что существует два различных случая отношений между старшим ![]() и верхним центральным
и верхним центральным ![]() показателями линейных систем:
показателями линейных систем: ![]() . На примере заданной линейной однородной диагональной системы дифференциальных уравнений подробно рассмотрены вычисления характеристического показателя Ляпунова, спектра, старшего и верхнего центрального показателей.
. На примере заданной линейной однородной диагональной системы дифференциальных уравнений подробно рассмотрены вычисления характеристического показателя Ляпунова, спектра, старшего и верхнего центрального показателей.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Б.П. Демидович, Лекции по математической теории устойчивости.-
Москва, «Наука», 1967г.
2. Б.Ф. Былов, Р.Э. Виноград, Д.М. Гробман, В.В. Немыцкий, Теория
показателей Ляпунова и ее приложения к вопросам устойчивости.- Москва, «Наука», 1966г.
3. Р.Э. Виноград, Оценка скачка старшего характеристического
показателя при малых возмущениях.-Докл. АН СССР, 1957г., т.114, №3, с.459-461.
4. В.М. Миллионщиков, Доказательство достижимости центральных показателей линейных систем.- Сиб. мат.ж., 1969г., т.10, №1, с.99-104.
5. Р.Э. Виноград, О центральном характеристическом показателе системы дифференциальных уравнений.- Матем.сб., 1957г., т.42(84), С.207-222.
Похожие работы
... 1. высокий уровень – 0% 2. средний уровень – 20% 3. низкий уровень – 80% Глава 3. Специфические особенности использования изобразительной деятельности для коррекции речевого недоразвития и формирования мелкой моторики у старших дошкольников с дизартрией 3.1 Методика обучающего эксперимента Цель: создать условия для коррекции речевого недоразвития и развития мелкой моторики кисти ...
... ущерб качеству решения задачи. Приоритетно для этой группы общественное признание, которое влияет на самооценку, но не является определяющим ее фактором. Важным аспектом для совершенствования системы стимулирования персонала в гостинице «Пулковская» является не столько группировка сотрудников по психотипам, сколько определение наиболее эффективных вариантов отношений между сотрудниками с учетом ...
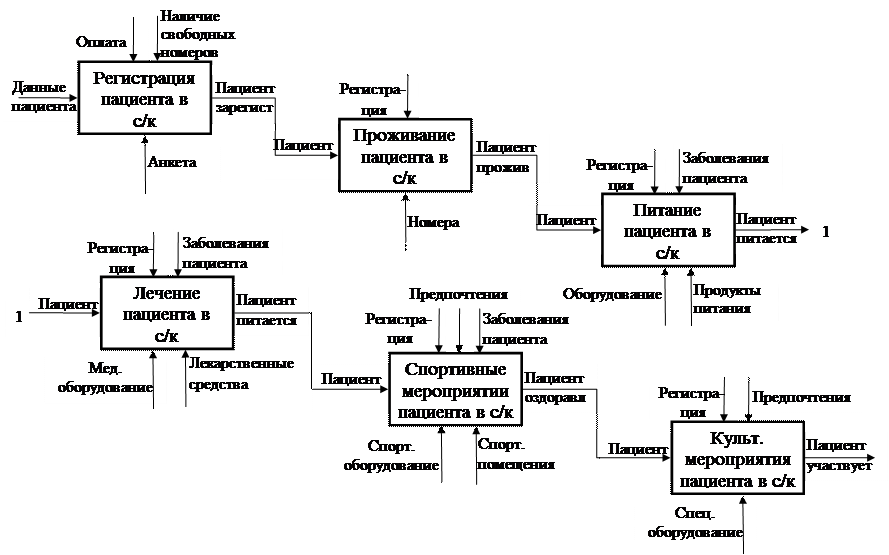
... график. Также просчитана общая стоимость разрабатываемой базы данных и оценена качественная эффективность автоматизированной подсистемы. ГЛАВА 6 ЭКОЛОГИЯ И ОХРАНА ТРУДА Автоматизированная система управления подсистемой «Диетпитание» санаторного комплекса «Валуево», которая разрабатывается в дипломном проекте, представляет собой электронный офис. ...
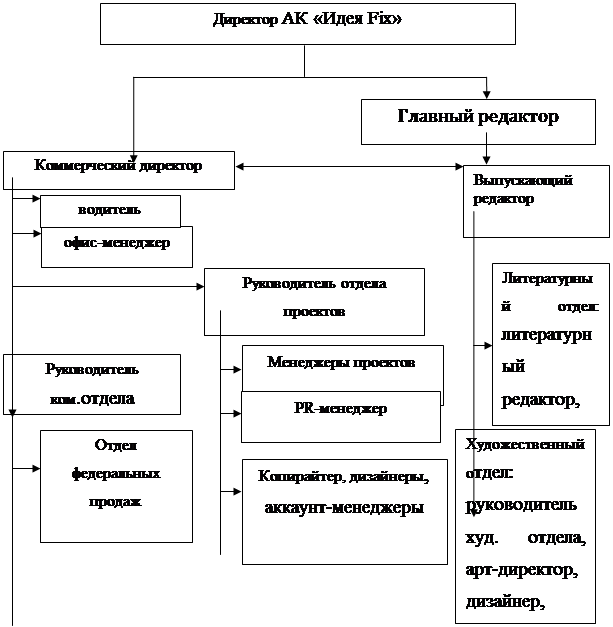
... дипломного проекта подлежит компания ООО АК «Идея Fix» и, соответственно, все вышеперечисленные задачи будут решаться на примере указанного предприятия и его продукта, рекламно-информационного журнала «LюMON». 2. АНАЛИЗ И ПРОЕКТИРОВАНИЕ СИСТЕМЫ ПРОДВИЖЕНИЯ ПРОДУКЦИИ НА ПРИМЕРЕ АК «ИДЕЯ-FIX» 2.1 Общая характеристика АК «Идея Fix» Агентство коммуникаций «Идея Fix» существует с 2004 года и ...





0 комментариев