Навигация
Вспомогательные определения
2. Вспомогательные определения
Комплексные числа- числа вида х + iy, где х и у — действительные числа, а i — так называемая мнимая единица (число, квадрат которого равен —1); х называют действительной частью, а у — мнимой частью.
Размерность пространства: векторное пространство ![]() над полем F называется
над полем F называется ![]() -мерным, если в нем существуют
-мерным, если в нем существуют ![]() линейно независимых векторов, а любые
линейно независимых векторов, а любые ![]() векторов уже являются линейно зависимыми. При этом число
векторов уже являются линейно зависимыми. При этом число ![]() называется размерностью пространства
называется размерностью пространства ![]() . Размерность пространства
. Размерность пространства ![]() обычно обозначают символом
обычно обозначают символом ![]() .
.
n-мерное Евклидово пространство над полем F: Вещественное векторное пространство ![]() называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования:
называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования:
Имеется правило, посредством которого любым двум элементам этого пространства ![]() и
и ![]() ставится в соответствие вещественное число, называемое скалярным произведением этих элементов (и обозначаемое символом
ставится в соответствие вещественное число, называемое скалярным произведением этих элементов (и обозначаемое символом ![]() ).
).
Указанное правило подчинено следующим четырем аксиомам:
![]() (коммутативность или симметрия);
(коммутативность или симметрия);
![]() (дистрибутивность скалярного произведения относительно сложения);
(дистрибутивность скалярного произведения относительно сложения);
![]()
![]() ;
;
![]() , если
, если ![]() ;
; ![]() , если
, если ![]() .
.
Подпространство- такое подмножество пространства L, которое само является пространством.
Ортонормированный базис: Говорят, что ![]() элементов
элементов ![]()
![]() -мерного евклидова пространства
-мерного евклидова пространства ![]() образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из них равна единице, т.е. если
образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из них равна единице, т.е. если
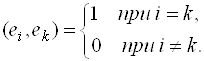
Билинейное отображение: Пусть L-линейное пространство над полем Р. Тогда отображение ![]() называется билинейным, если
называется билинейным, если
![]() ,
, ![]()
![]()
Сюръективное отображение- отображение ![]() , которое каждому элементу из
, которое каждому элементу из ![]() сопоставляет, по крайней мере, один прообраз, т.е.
сопоставляет, по крайней мере, один прообраз, т.е. ![]() .
.
Ядро: Пусть ![]() - гомоморфизм кольца R в кольцо S. Множество
- гомоморфизм кольца R в кольцо S. Множество ![]() , где 0’-нуль в S, -ядро.
, где 0’-нуль в S, -ядро.
Обратимая матрица-матрица, для которой существует обратная матрица.
Невырожденная матрица - квадратная матрица, определитель которой отличен от нуля.
Симметричная матрица - матрица является симметричной, если она совпадает со своей транспонированной матрицей (т.е. A = A'). Другими словами, нижний треугольник квадратной матрицы является "зеркальным отражением" верхнего треугольника.
Характеристика поля - пусть P-поле. Если существует такое целое положительное n, что для каждого ![]() выполняется равенство n·r=0, то наименьшее из таких чисел n называется характеристикой поля P. Обозначение - char P.
выполняется равенство n·r=0, то наименьшее из таких чисел n называется характеристикой поля P. Обозначение - char P.
Кососимметричная матрица- квадратная матрица А над полем P характеристики ![]() такая, что
такая, что![]() , где
, где ![]() — транспонированная матрица.
— транспонированная матрица.
Линейная независимость системы векторов: Система векторов ![]() называется линейно независимой, если существует только тривиальная линейная комбинация данных векторов равная нулевому вектору.
называется линейно независимой, если существует только тривиальная линейная комбинация данных векторов равная нулевому вектору.
Похожие работы
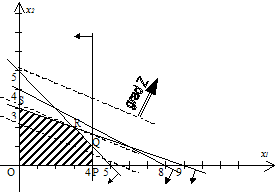
... стратегии игрока В. Задача имеет решение игры, если её матрицы не содержит седловой точки (). Расчет выигрышей производится по целевой функции: Система ограничения: 2.3.Описания метода Гурвица 2.3.1. Выбираем по строкам наименьший выигрыш и заполняем колонку а. 2.3.2. Выбираем по строкам наибольший выигрыши и заполняем колонку 2.3.3. Производим расчёт выигрыша по формуле: ; ...
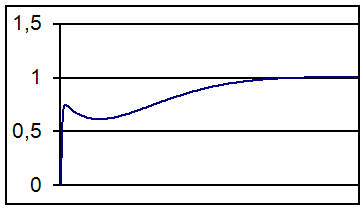
... процесс является колебательным и имеет А1 и А3 (первая и третья амплитуды переходного процесса), то можно найти и степень затухания. 6. Функциональная схема Системы Автоматического Управления в общем виде выглядит следующим образом: 7. Вывод Математическая модель объекта регулирования системы, полученная в работе, является достаточно адекватной исходным данным. Об ...
... , чем обычно. Общий заработок в 1000 $ они должны поделить следующим образом: певцу 350 $, пианисту 435 $, ударнику 175 $. Глава . Принятие решений в условиях частичной неопределенности. Элементы теории статистических решений. Предметом рассмотрения данного раздела служат статистические модели приянятия решений, трактуемые как статистические игры или игры с природой при использовании ...
... какая-либо из имеющихся. ж) Придумайте взвешивающую формулу (ее придется объяснить при защите курсовой работы!) и найдите по ней худшую и лучшую операции. 18. Произвести математико-статистический анализ за T лет Xt, Kt, Lt (t = 1, …, T) о выпуске продукции (в стоимостном виде), ОПФ и числе занятых исследуемого производственного экономического объекта: а) найти прогноз выпуска, фондов ...

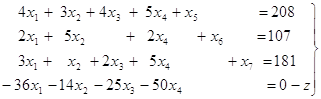

0 комментариев