Навигация
4. Вопрос Гурвица
Вернемся к формулам с суммами квадратов. Теперь нас интересует такая алгебраическая задача: какие формулы с суммами квадратов можно написать для случая многих переменных? Сформулируем эту задачу более точно. Рассмотрим формулу вида
(2),
в которой все 
- билинейные комбинации переменных 
и 
. Билинейные комбинации-выражения вида 
и т.д., а также суммы таких выражений, взятых с произвольными действительными коэффициентами. Формулу (2) будем называть формулой типа (r,s,n).
Существует формула типа (4, 4, 4). Это связано со знаменитой алгеброй кватернионов, построенной Уильямом Роуэном Гамильтоном (1806—1865, ирландский математик).
, где
,
,
,
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
0 -1 0 0 ,
= 1 0 0 0 , 
0 0 0 -1 , 
0 0 1 0
0 0 -1 0 0 0 0 1 1 0 0 0 0 -1 0 0
0 0 0 -1 0 0 -1 0 0 1 0 0 1 0 0 0
Комплексные числа удобно отождествлять с точками плоскости, поскольку они имеют две координаты – вещественную часть и мнимую. По аналогии с комплексными числами, Гамильтон долго пытался построить «трехмерные числа», т.е. наделить точки трехмерного пространства естественными операциями сложения и умножения, удовлетворяющими некоторым естественным свойствам. Однако, ему это не удалось. Более того, в некотором естественном смысле, таких «хороших» операций не существует. Все же поиски были не бесполезны. В результате своих поисков Гамильтон наткнулся на замечательную и естественную конструкцию «четырехмерных» чисел – кватернионов.
Кватернионом называется выражение вида
,
в котором i, j, k – формальные символы, не являющиеся действительными числами. Эти символы удовлетворяют следующим соотношениям:
, 
, 
Первая серия соотношений состоит в том, что каждое из чисел i, j, k является мнимой единицей. Вторая серия соотношений содержит 2 вещи. Первая – мнимые единицы i, j, k антикоммутируют. Кроме этого, вторая серия соотношений выражает произведение любых двух мнимых единиц из трех указанных через эти же самые мнимые единицы. Как складывать и перемножать произвольные кватернионы? Для этого нужно воспользоваться правилами умножения мнимых единиц i, j, k, а также всеми обычными законами сложения и обычным законом дистрибутивности. Например,
Теорема 2: Умножение кватернионов ассоциативно, т.е. для любых трех кватернионов 
выполнено равенство 
Кватернион 
называется сопряжённым к 
.
Так же, как и для комплексных чисел,
называется модулем q (или нормой q).
Теорема 3: Для любой пары кватернионов 
выполнено соотношение
Доказательство:
Эту формулу можно интерпретировать как формулу типа (4, 4, 4) для произведения сумм квадратов.
Формула типа (8, 8, 8) была найдена в 1845 году английским математиком А.Кэли.
А. Гурвиц в 1898 году поставил следующий вопрос, который до сих пор является открытым: Для каких целых чисел r, n, s существует формула типа (r, s, n) для произведения сумм квадратов?
Этот вопрос имеет несколько вариантов. В формуле типа (r, s, n) сумма квадратов r переменных, умноженная на сумму квадратов s переменных, представляется в виде суммы квадратов n билинейных форм от этих двух групп переменных. Однако коэффициенты в этих билинейных формах могут быть целыми, вещественными, комплексными и т.п. Ни в одной из этих ситуаций, на вопрос Гурвица не найдено полного ответа. Кажется, что ответ должен зависеть от выбора коэффициентов. Для всех известных примеров формул с комплексными коэффициентами, существуют формулы того же типа с вещественными и даже целыми коэффициентами.
Похожие работы
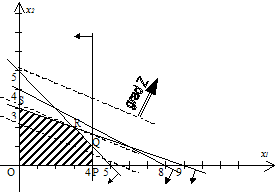
... стратегии игрока В. Задача имеет решение игры, если её матрицы не содержит седловой точки (). Расчет выигрышей производится по целевой функции: Система ограничения: 2.3.Описания метода Гурвица 2.3.1. Выбираем по строкам наименьший выигрыш и заполняем колонку а. 2.3.2. Выбираем по строкам наибольший выигрыши и заполняем колонку 2.3.3. Производим расчёт выигрыша по формуле: ; ...
... процесс является колебательным и имеет А1 и А3 (первая и третья амплитуды переходного процесса), то можно найти и степень затухания. 6. Функциональная схема Системы Автоматического Управления в общем виде выглядит следующим образом: 7. Вывод Математическая модель объекта регулирования системы, полученная в работе, является достаточно адекватной исходным данным. Об ...
... , чем обычно. Общий заработок в 1000 $ они должны поделить следующим образом: певцу 350 $, пианисту 435 $, ударнику 175 $. Глава . Принятие решений в условиях частичной неопределенности. Элементы теории статистических решений. Предметом рассмотрения данного раздела служат статистические модели приянятия решений, трактуемые как статистические игры или игры с природой при использовании ...
... какая-либо из имеющихся. ж) Придумайте взвешивающую формулу (ее придется объяснить при защите курсовой работы!) и найдите по ней худшую и лучшую операции. 18. Произвести математико-статистический анализ за T лет Xt, Kt, Lt (t = 1, …, T) о выпуске продукции (в стоимостном виде), ОПФ и числе занятых исследуемого производственного экономического объекта: а) найти прогноз выпуска, фондов ...
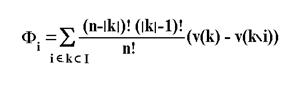
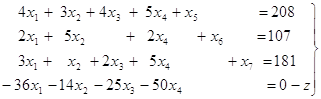
0 комментариев