Навигация
Раскрыть некоторые основы теории линейных операторов, необходимые для освоения методов решения операторных уравнений;
1. раскрыть некоторые основы теории линейных операторов, необходимые для освоения методов решения операторных уравнений;
2. проиллюстрировать на конкретных примерах способы решения операторных уравнений и дать пояснения по ходу решения конкретных задач.
Так как выделение из функционального анализа его прикладной части, содержащей конструктивные методы получения решений задач, преследует методическую цель – сделать эти методы доступнее тем, кто занимается приложениями математики. Поэтому данная работа разделена на две главы, в первой содержатся необходимые теоретические обоснования способов решения операторных уравнений и суть обоих методов, а во второй – решения конкретных задач.Глава 1. Операторные уравнения §1.Определение линейного оператора
Пусть X и Y – линейные пространства, оба вещественные или оба комплексные.
Оператор А: X → Y с областью определения D(А) называется линейным, если
А(λ1x1 + λ2x2) = λ1А(x1) + λ2А(x2)
для любых x1,x2 Î D и любых скаляров λ1 и λ2.
Пусть X и Y – нормированные пространства и А: X → Y, где А – линейный оператор, всюду заданный в X (т.е. D(А) = X).
Оператор А называется непрерывным в точке x0 Î X, если Аx → Аx0 при x → x0. Но судить о непрерывности линейного оператора в различных точках x0 Î X можно по непрерывности его в нуле пространства X.
Теорема 1. Пусть линейный оператор А всюду задан в банаховом пространстве X и со значениями в банаховом пространстве Y непрерывен в точке 0 Î X; тогда А непрерывен в любой точке x0 Î X.
Доказательство. Рассмотрим равенство Аx – Аx0 = А (x – x0). Если x → x0, то z = x – x0 → 0. По непрерывности в нуле Аz → 0, но тогда Аx – Аx0 → 0, что и требовалось доказать.
Линейный оператор А называется непрерывным, если он непрерывен в точке x = 0.
Пусть S1(0) – замкнутый шар ||x|| ≤ 1 в банаховом пространстве X.
Будем называть линейный оператор А: X → Y ограниченным, если он ограничен на единичным шаре S1(0), т.е. если ограничено множество
{ ||Аx||, ||x|| ≤ 1}.
Согласно определению, если А ограничен, то существует постоянная с > 0 такая, что для любых x с ||x|| ≤ 1 справедливо неравенство
||Аx|| ≤ с (1)
Теорема 2. А ограничен тогда и только тогда, когда справедлива оценка
||Аx|| ≤ с ||x|| (2)
для любых x Î X, где с – постоянная.
Теорема 3. Пусть А: X → Y, А – линейный оператор, X, Y – банаховы пространства. Для того чтобы А был непрерывным, необходимо и достаточно, чтобы он был ограниченным.
§2. Норма линейного оператораВ линейном пространстве непрерывных линейных операторов зададим норму следующим образом:
![]() . (1)
. (1)
Поясним, почему существует конечное число ||А||, определяемое для любого ограниченного оператора равенством (1). Так как А – ограничен, то множество
![]()
ограничено сверху. По теореме о верхней грани существует ![]() .
.
Из свойства sup M следует, что ||Аx|| ≤ ||А|| для всех x Î S1(0). Отсюда
||Аx|| ≤ ||А|| ||x||, (2)
справедливое для всех x Î X, включая x = 0. таким образом, ||А|| является наименьшей из констант в неравенстве ||Аx|| ≤ ||А||, и, значит, оценка (2) является наилучшей.
Пространство нормированных непрерывных линейных операторов, действующих из X в Y, будем обозначать L(X, Y).
§3.Обратные операторыСистемы линейных алгебраических уравнений, интегральные уравнения, а также различные задачи для обыкновенных дифференциальных уравнений и уравнений с производными часто могут быть записаны в виде линейного уравнения
![]()
Если существует обратный оператор ![]() , то решение задачи записывается в явном виде:
, то решение задачи записывается в явном виде:
![]()
Важное значение приобретает теперь выявление условий, при выполнении которых обратный оператор существует и обладает теми или иными свойствами.
Пусть задан линейный оператор: А: X → Y, где X,Y – линейные пространства, причем его область определения D(A)![]() X, а область значений R(A)
X, а область значений R(A)![]() Y.
Y.
Введем множество ![]() - множество нулей оператора А. заметим, что N(A) не пусто, так как 0 Î N(A)
- множество нулей оператора А. заметим, что N(A) не пусто, так как 0 Î N(A)
Теорема 4. Оператор А переводит D (А) в R (А) взаимно однозначно тогда и только тогда, когда N(A)=![]() , (т.е. множество А нулей состоит только из элемента 0)
, (т.е. множество А нулей состоит только из элемента 0)
Теорема 5. Оператор А-1 существует и ограничен на R(A) тогда и только тогда, когда для некоторой постоянной m>0 и любого x Î D(A) выполняется неравенство
![]() . (1)
. (1)
Введем теперь следующее важное понятие.
Будем говорить, что линейный оператор А: X → Y непрерывно обратим, если R(A)=Y , оператор обратим и A-1 Î L(Y, X), (т.е. ограничен).
Обращаясь к теореме 5, мы сможем сформулировать следующее утверждение.
Теорема 6. Оператор А непрерывно обратим тогда и только тогда, когда R(A)=Y и для некоторой постоянной m>0 и для всех ![]() выполняется неравенство (1).
выполняется неравенство (1).
В случае определенного и ограниченного на всем множестве оператора A Î L(X,Y) имеется теорема Банаха об обратном операторе.
Теорема 7. Если А – ограниченный линейный оператор, отображающий взаимно однозначно банахово пространство X на банахово пространство Y, то обратный оператор А-1 ограничен.
Иными словами, если А Î L(X,Y), где X и Y банаховы, R(A)=Y и А обратим, то А непрерывно обратим.
Взглянем на понятие непрерывно обратимого оператора с точки зрения разрешимости линейного уравнения
Ax = y (2)
Если А непрерывно обратим, то уравнение это имеет единственное решение x = A-1y для любой правой части у. Если при этом ![]() (решение того же уравнения с правой частью
(решение того же уравнения с правой частью ![]() ), то
), то ![]() . Это означает, что малое изменение правой части y влечет малое изменение решения, или, как принято говорить, задача (2) корректно разрешима.
. Это означает, что малое изменение правой части y влечет малое изменение решения, или, как принято говорить, задача (2) корректно разрешима.
Пусть А Î L(X,Y). Оператор U Î L(X,Y) будем называть правым обратным к А, если AU = Iy. Оператор V Î L(X,Y) будем называть левым обратным к А, если VA = Ix.
Здесь через Iy (Ix) обозначен тождественный оператор в пространстве Y (X). Ниже для правого обратного к А используем обозначение Аr–1, а для левого – АL–1.
Лемма 1. Если существует правый обратный Аr–1 к А, то уравнение (2) имеет решение
x = Аr–1 y
Если существует левый обратный оператор к А, то уравнение (2) может иметь не более одного решения.
Доказательство.
А(Аr–1 y) = (А Аr–1)y = y,
т.е. x = Аr–1 y обращает (2) в тождество и, значит, является решением.
Далее, пусть существует АL–1. рассмотрим N(A). Пусть x Î N(A), тогда Аx = 0. применим к этому равенству оператор АL–1, тогда АL–1Аx = 0, откуда x = 0. итак, всякое x Î N(A) оказывается равным 0. Значит, N(A) = {0} и, по теореме 4, А взаимно однозначен, т.е. для уравнения (2) справедлива теорема единственности. Что и требовалось доказать.
Пусть X – банахово пространство. Рассмотрим банахово пространство L(X) – пространство линейных, ограниченных и заданных на всем множестве операторов. Пусть I – тождественный оператор в L(X). Очевидно, что I непрерывно обратим. Ниже доказывается, что вместе с I непрерывно обратимы все операторы ![]() - единичного шара в L(X), т.е. все такие А, для которых справедливо неравенство
- единичного шара в L(X), т.е. все такие А, для которых справедливо неравенство ![]() .
.
Для краткости положим C = I – A. Ниже мы будем ссылаться на признак Вейерштрасса: пусть X – банахово пространство, тогда всякий абсолютно сходящийся в X ряд сходится.
Теорема 8. Пусть ![]() и
и ![]() ; тогда оператор I – C непрерывно обратим. При этом справедливы оценки
; тогда оператор I – C непрерывно обратим. При этом справедливы оценки
![]() (1)
(1)
![]() (2)
(2)
Доказательство. Рассмотрим в L(X) ряд
I+C+C2+C3+… (3)
Так как ![]() , то ряд (3) оценивается сходящимся числовым рядом – геометрической прогрессией
, то ряд (3) оценивается сходящимся числовым рядом – геометрической прогрессией
![]()
По признаку Вейерштрасса ряд (3) сходится равномерно, т.е.
![]() .
.
Где S – сумма ряда (3). Далее простой проверкой убеждаемся, что
![]() ,
,
![]() .
.
Но при этом ![]() (ибо
(ибо ![]() и
и ![]() ), а
), а ![]() . Поэтому, в пределе имеем равенства (I – C)S = I и S(I – C) = I. По лемме 1 отсюда заключаем, что I – C непрерывно обратим и S=(I – C)-1. Далее,
. Поэтому, в пределе имеем равенства (I – C)S = I и S(I – C) = I. По лемме 1 отсюда заключаем, что I – C непрерывно обратим и S=(I – C)-1. Далее,
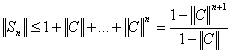 ,
,
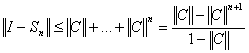 .
.
Переходя в этих неравенствах к пределу при ![]() , получаем оценки (1) и (2). Теорема доказана.
, получаем оценки (1) и (2). Теорема доказана.
Теперь рассмотрим более общий случай пространства L(X,Y). Пусть А Î L(X,Y) непрерывно обратим.
Теорема 9. Пусть A, B Î L(X,Y), А непрерывно обратим и выполнено неравенство ![]() . Тогда B непрерывно обратим и справедливы оценки
. Тогда B непрерывно обратим и справедливы оценки
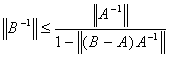 ,
, 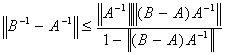 .
.
Пусть S – некоторое множество на числовой оси или в комплексной плоскости, а X – нормированное пространство.
Рассмотрим функцию x(![]() ) с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции.
) с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции.
Пусть x(![]() ) определена в окрестности точки
) определена в окрестности точки ![]() 0, за исключением, быть может, самой точки
0, за исключением, быть может, самой точки ![]() 0. Элемент а Î X будем называть пределом функции x(
0. Элемент а Î X будем называть пределом функции x(![]() ) при
) при ![]() →
→![]() 0 и записывать
0 и записывать
![]() при
при ![]() →
→![]() 0,
0,
если ![]() при
при ![]() →
→![]() 0.
0.
Степенные ряды – это специальный случай рядов в нормированном пространстве, когда члены ряда зависят от параметра![]() .
.
Рассмотрим в нормированном пространстве X ряд вида ![]() , где xк Î X, а
, где xк Î X, а ![]() – вещественное или комплексное переменное. Поскольку можно ввести новую переменную
– вещественное или комплексное переменное. Поскольку можно ввести новую переменную ![]() –
–![]() 0 =
0 = ![]() , то в дальнейшем мы полагаем
, то в дальнейшем мы полагаем ![]() 0 = 0 и рассматриваем степенные ряды вида
0 = 0 и рассматриваем степенные ряды вида
![]() (1)
(1)
Конечная сумма ![]() называется частичной суммой степенного ряда (1).
называется частичной суммой степенного ряда (1).
Пусть ![]() – множество всех точек
– множество всех точек ![]() , для которых ряд (1) сходится.
, для которых ряд (1) сходится. ![]() называется областью сходимости ряда (1).
называется областью сходимости ряда (1).
Сумму ряда (1) при ![]() Î
Î ![]() обозначим через S(
обозначим через S(![]() ) (это абстрактная функция, определенная на
) (это абстрактная функция, определенная на ![]() со значениями в X), при этом будем писать
со значениями в X), при этом будем писать
![]()
![]() , при
, при ![]() Î
Î ![]() .
.
Последнее равенство означает, что Sn(![]() ) → S(
) → S(![]() ) при n→∞ для всех
) при n→∞ для всех ![]() Î
Î ![]() .
.
Очевидно, область сходимости любого степенного ряда (1) не пуста, так как 0 Î ![]() . Как и в случае скалярных функций, справедлива следующая теорема.
. Как и в случае скалярных функций, справедлива следующая теорема.
Теорема 10 (Абель). Пусть![]() 0 ≠ 0 и
0 ≠ 0 и ![]() 0 Î
0 Î ![]() , тогда круг
, тогда круг ![]() содержится в
содержится в ![]() . Во всяком круге Sr(0), где r <
. Во всяком круге Sr(0), где r < ![]() , ряд (1) сходиться абсолютно и равномерно относительно
, ряд (1) сходиться абсолютно и равномерно относительно ![]() .
.
Теорема 11. Пусть два степенных ряда равны в круге SR(0), R>0:
![]()
![]() ;
;
тогда равны все их коэффициенты: ![]() (k=0, 1, 2, …)
(k=0, 1, 2, …)
Дифференцирование абстрактных функций
Пусть функция ![]() числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.
числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.
По определению производной x’(λ0) функции x(λ) в точке λ0 называется предел
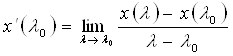 ,
,
если этот предел существует (и конечен). Если ![]() имеет производную в точке λ0, то она называется дифференцируемой в этой точке.
имеет производную в точке λ0, то она называется дифференцируемой в этой точке.
Абстрактную функцию x(![]() ) будем называть аналитической при
) будем называть аналитической при ![]() =0, если она представима в некоторой окрестности точки
=0, если она представима в некоторой окрестности точки ![]() =0 сходящимся степенным рядом:
=0 сходящимся степенным рядом:
![]() (1)
(1)
с ненулевым радиусом сходимости.
Теорема 12. Если x(![]() ) – аналитическая абстрактная функция при
) – аналитическая абстрактная функция при ![]() =0, то x(
=0, то x(![]() ) непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).
) непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).
Теорема 13. Если x(![]() ) – аналитическая абстрактная функция при
) – аналитическая абстрактная функция при ![]() =0, то x(
=0, то x(![]() ) дифференцируема в круге SR(0) сходимости своего степенного разложения.
) дифференцируема в круге SR(0) сходимости своего степенного разложения.
Пусть x(![]() ) бесконечно дифференцируема в точке 0. Ряд вида
) бесконечно дифференцируема в точке 0. Ряд вида
![]()
называется рядом Тейлора функции x(![]() ).
).
Если x(![]() ) аналитична при
) аналитична при ![]() =0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0).
=0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0).
Понятие абстрактной аналитической функции используется в широко применяемом на практике методе малого параметра.
§6. Метод малого параметра в простейшем случаеРассмотрим следующее уравнение:
Аx –![]() Сx=y. (1)
Сx=y. (1)
Здесь А, С Î L(X,Y) и y Î Y заданы, ![]() - скалярный параметр,
- скалярный параметр, ![]() , а неизвестное x разыскивается в X. Если
, а неизвестное x разыскивается в X. Если ![]() , т.е.
, т.е.
![]() , (2)
, (2)
то, согласно теореме 9, оператор А–![]() С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой
С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой
![]() . (3)
. (3)
Отсюда видно, что в круге (2) решение является аналитической функцией параметра ![]() и, следовательно, может быть найдено в виде
и, следовательно, может быть найдено в виде
![]() (4)
(4)
На этой идее основывается метод малого параметра для уравнения (1). Подставим ряд (4) в уравнение (1) и, согласно теореме единственности разложения в степенной ряд, приравниваем коэффициенты при одинаковых степенях ![]() в правой и левой частях получившегося тождества:
в правой и левой частях получившегося тождества:
![]() .
.
Таким образом, мы приходим к следующей рекуррентной системе уравнений для определения x0, x1, …:
Аx0=y, Аx1=Сx0, …, Аxк=Сxк-1, …
Так как А непрерывно обратим, то отсюда последовательно находим
x0=А–1y, x1= А–1(СА–1)y, …, xк= А–1(СА–1)кy, …
Следовательно,
![]() . (5)
. (5)
Мы получили решение (3), разложенное в степенной ряд. Если мы хотим оборвать степенной ряд и ограничиться приближенным решением
![]()
то можно оценить ошибку. Вычитая из ряда (5) его частичную сумму (6) и оценивая разность по норме, получим
 .
.
Пусть дано уравнение
А(![]() )х = у(
)х = у(![]() ). (1)
). (1)
Здесь А(![]() )Î L(X,Y) задана при каждом
)Î L(X,Y) задана при каждом ![]() ,
, ![]() , или, как говорят, А(
, или, как говорят, А(![]() ) – оператор-функция. Пусть А(
) – оператор-функция. Пусть А(![]() ) аналитична при
) аналитична при ![]() =0, а оператор А(0) непрерывно обратим, у(
=0, а оператор А(0) непрерывно обратим, у(![]() ) – заданная аналитическая функция
) – заданная аналитическая функция ![]() при
при ![]() =0 со значениями в Y. Неизвестное x разыскивается в X.
=0 со значениями в Y. Неизвестное x разыскивается в X.
Аналитичность А(![]() ) и у(
) и у(![]() ) в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны
) в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны ![]() и
и ![]() соответственно:
соответственно:
![]() ,
, ![]() . (2)
. (2)
Из аналитичности А(![]() ) следует непрерывность А(
) следует непрерывность А(![]() ) при
) при ![]() =0. следовательно, найдется число r > 0 такое, что в круге
=0. следовательно, найдется число r > 0 такое, что в круге ![]()
![]() .
.
Отсюда вытекает, что в круге ![]() оператор-функция А(
оператор-функция А(![]() ) непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение
) непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение
![]() ,
,
при этом x(![]() ) аналитична в точке
) аналитична в точке ![]() =0 и радиус сходимости соответствующего степенного ряда равен min(
=0 и радиус сходимости соответствующего степенного ряда равен min(![]() , r). Для фактического построения x(
, r). Для фактического построения x(![]() ) удобно воспользоваться методом малого параметра. Будем разыскивать x(
) удобно воспользоваться методом малого параметра. Будем разыскивать x(![]() ) в виде
) в виде
![]() . (3)
. (3)
Подставляя ряд (3) в уравнение (1) и учитывая разложения (2), приходим к следующей системе для неопределенных коэффициентов x0, x1, x2, …:
А0x0 = y0, А0x1+А1x0 = y1,
А0x2 + А1x1 + А2x0 = y2, (4)
. . . . . . . . . . .
![]() , …
, …
Здесь А0 = А(0) непрерывно обратим. Решая последовательно уравнения получившейся системы, находим
![]() ,
, ![]() , … (5)
, … (5)
Возникающие здесь формулы довольно громоздки, однако этим путем можно найти решение уравнения с любой степенью точности. Метод малого параметра особенно удобен в тех случаях, когда обращение оператора А(0) – задача более простая, чем задача обращения оператора А(![]() ).
).
В качестве еще одного приложения теорем об обратных операторах рассмотрим один из вариантов метода продолжения по параметру. Пусть ![]() и А непрерывно обратим. Если
и А непрерывно обратим. Если ![]() , то, согласно теореме 9 §3, В также непрерывно обратим. Оказывается, при определенных условиях можно доказать, что В будет непрерывно обратим и в том случае, когда он очень далек от А. Идея заключается в следующем. Рассмотрим непрерывную на отрезке [0, 1] оператор - функцию
, то, согласно теореме 9 §3, В также непрерывно обратим. Оказывается, при определенных условиях можно доказать, что В будет непрерывно обратим и в том случае, когда он очень далек от А. Идея заключается в следующем. Рассмотрим непрерывную на отрезке [0, 1] оператор - функцию ![]() такую, что А(0)=А, А(1)=В. Иначе говоря, в L(X, Y) рассматривается непрерывная кривая, соединяющая точки А и В. Будем предполагать, что для оператор – функции
такую, что А(0)=А, А(1)=В. Иначе говоря, в L(X, Y) рассматривается непрерывная кривая, соединяющая точки А и В. Будем предполагать, что для оператор – функции ![]() выполняется следующее условие:
выполняется следующее условие:
1. Существует постоянная ![]() такая, что при всех
такая, что при всех ![]() и при любых
и при любых ![]() справедливо неравенство
справедливо неравенство
![]() . (1)
. (1)
Ниже будет доказана следующая теорема.
Теорема 14. Пусть А(λ) – непрерывная на [0, 1] оператор-функция (при каждом ![]() ), причем оператор А(0) непрерывно обратим. Если для А(λ)выполняется условие I, то А(I)непрерывно обратим, причем
), причем оператор А(0) непрерывно обратим. Если для А(λ)выполняется условие I, то А(I)непрерывно обратим, причем ![]() .
.
Замечание к теореме 14. Если выполнено условие I при ![]() и оператор
и оператор ![]() непрерывно обратим, то
непрерывно обратим, то
![]() .
(2)
.
(2)
Действительно, пусть ![]() , а
, а ![]() , т.е.
, т.е.![]() . тогда условие I дает
. тогда условие I дает ![]() или
или ![]() , что означает справедливость неравенства (2).
, что означает справедливость неравенства (2).
Приведем здесь доказательство теоремы 14 для случая, когда ![]() . Согласно условию этой теоремы
. Согласно условию этой теоремы ![]() . По замечанию 14
. По замечанию 14 ![]() . Имеем следующую оценку:
. Имеем следующую оценку:
![]() .
.
Пусть ![]() , где
, где ![]() . На [0, δ] имеем
. На [0, δ] имеем ![]() , и, следовательно, по теореме 9 А(λ) при всяком
, и, следовательно, по теореме 9 А(λ) при всяком ![]() непрерывно обратим. Если окажется, то
непрерывно обратим. Если окажется, то ![]() , то теорема доказана.
, то теорема доказана.
Пусть δ < 1. Возьмем А(δ). Согласно замечанию п.14.1 ![]() . Повторяем наши рассуждения при λ>δ. Имеем оценку
. Повторяем наши рассуждения при λ>δ. Имеем оценку
![]() ,
,
если ![]() , откуда А(λ) непрерывно обратим при каждом
, откуда А(λ) непрерывно обратим при каждом ![]() . Если
. Если ![]()
![]() , то теорема доказана. Если же 2δ < 1, то
, то теорема доказана. Если же 2δ < 1, то ![]() и рассуждение можно повторить. После конечного числа шагов мы достигаем точки λ=1, и, следовательно, А(1) непрерывно обратим.
и рассуждение можно повторить. После конечного числа шагов мы достигаем точки λ=1, и, следовательно, А(1) непрерывно обратим.
Доказательство теоремы в общем случае
Рассмотренный выше частный случай отрезка в L(X,Y) не всегда удобен в приложениях. Общий случай основывается на следующем элементарном предложении.
Лемма. Пусть М – некоторое непустое множество на [0,1], одновременно открытое и замкнутое на [0.1]. тогда М=[0, 1].
Замечание 1. условие открытости М на [0,1] понимается так: для любого ![]() существует δ > 0 такое, что
существует δ > 0 такое, что ![]() .
.
Доказательство леммы. Пусть N = [0, 1] \ M (дополнение к М на [0, 1]). Нужно доказать, что N = Æ – пустое множество. Допустим противное, что N ¹ Æ. Поскольку М ¹ Æ и ограничено сверху, то существует b = supM, причем b Î M вследствие замкнутости. Покажем, что b = 1. Если b <1, то вследствие открытости M на [0, 1] найдется x > b, x Î M. Это противоречит определению supM. Следовательно, b >1 невозможно. Итак, 1Î М.
Теперь рассмотрим множество N. Как дополнение к М, оно также открыто и замкнуто на [0, 1], и, значит, к нему применимо рассуждение с supM . мы получаем, что 1 Î N. Это невозможно, ибо N – дополнение к М. полученное противоречие доказывает, что допущение N ¹ Æ неверно. Итак, N= Æ, т.е. М = [0, 1]. Лемма доказана.
Вернемся к доказательству теоремы. Пусть М – множество тех точек λÎ[0, 1], для которых оператор А(λ) непрерывно обратим. Согласно замечанию 1 ![]() для всех λ Î М. М не пусто, поскольку 0 Î [0, 1].
для всех λ Î М. М не пусто, поскольку 0 Î [0, 1].
![]()
воспользуемся непрерывностью оператор–функции А(λ) в метрике L(X,Y). Для любого e > 0 найдется δ = δ(e)>0 такое, что при всех λ Î [0, 1] таких, что ![]() < δ выполняется неравенство
< δ выполняется неравенство ![]() <e.
<e.
Возьмем e = γ, тогда при ![]() < δ(γ), λ Î [0, 1]
< δ(γ), λ Î [0, 1]
![]() <1.
<1.
По теореме 9 §3 А(λ) непрерывно обратим для всех таких λ. Итак, вместе с λ0
М содержит ![]() , т.е. М открыто на [0, 1].
, т.е. М открыто на [0, 1].
Докажем, что М замкнуто на [0, 1]. Пусть ![]() и
и ![]() при
при ![]() . Надо доказать, что λ0
М. воспользуемся неравенством
. Надо доказать, что λ0
М. воспользуемся неравенством ![]() и получим
и получим
![]() .
.
Вследствие непрерывности А(λ) по λ для любого e > 0 находим номер N = N(e) такой, что при n > N будет ![]() <e. Возьмем e = γ, тогда для n = N(γ)+1
<e. Возьмем e = γ, тогда для n = N(γ)+1 ![]() <1.
<1.
По теореме 9 А(λ0) непрерывно обратим, т.е. λ0 Î М, и, значит, М замкнуто на [0, 1]. По лемме М = [0, 1] . в частности, 1Î М и ![]() . Теорема полностью доказана.
. Теорема полностью доказана.
Замечание. Рассмотрим уравнение с параметром:
А(λ)х = у, λÎ [0, 1]. (1*)
Пусть для всех возможных решений этого уравнения при всяком λÎ [0, 1] справедлива оценка
![]() , (2*)
, (2*)
где с – некоторая постоянная, не зависящая от х, у и λ. Оценка такого рода называется априорной оценкой для решения уравнения (1*). Очевидно, априорная оценка (2*) представляет собой лишь иначе записанное условие (1): ![]() .
.
Доказанная выше теорема свидетельствует о важности априорных оценок для доказательства теорем существования и единственности решений.
Глава 2. Приложение
Пример 1. Рассмотрим интегральное уравнение с малым вещественным параметром λ:
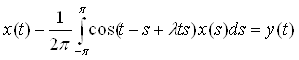 (1)
(1)
Это уравнение вида А(![]() )х = у(
)х = у(![]() ) – операторное уравнение в С[-π; π], где
) – операторное уравнение в С[-π; π], где
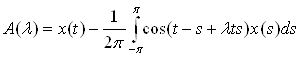
Покажем, что А(![]() ) аналитична в т. 0, т.е. разлагается в ряд вида
) аналитична в т. 0, т.е. разлагается в ряд вида ![]() . Разложим функцию А(
. Разложим функцию А(![]() ) в ряд Тейлора:
) в ряд Тейлора: ![]() .
.
Найдем к – ую производную:
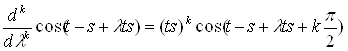
Разложим функцию в ряд Тейлора в т. 0:
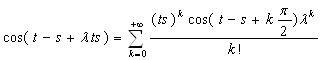
Таким образом, функция аналитична, следовательно, непрерывна при ![]() = 0, а значит, уравнение имеет единственное решение.
= 0, а значит, уравнение имеет единственное решение.
Операторные коэффициенты имеют вид:
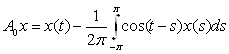 ;
; 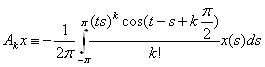 (2)
(2)
I. Начнем с уравнения А0x0 = y системы (4) §7, где у нас теперь y0=y, yк=0, к ≥ 1.

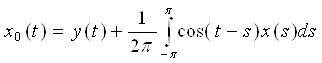
Заменим, ![]() , поэтому
, поэтому ![]()
![]() , (4)
, (4)
где
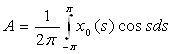 ,
, 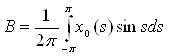
Для того, чтобы найти коэффициент А в уравнении (4), умножим его на cos t и, интегрируем по t от –π до π:
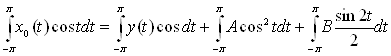 ,
,
подсчитаем интегралы:
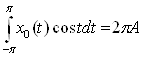 ,
, 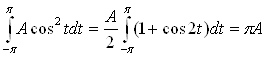 ,
, 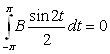
Тогда, подставив в уравнение, получаем: ![]() . Отсюда:
. Отсюда:
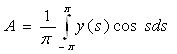 . (5)
. (5)
Найдем коэффициент В уравнения (4), умножив это уравнение на sin t и интегрируя по t от –π до π:
 .
.
Подсчитав соответствующие интегралы:
![]()
![]()
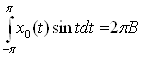 ,
, 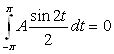 ,
, 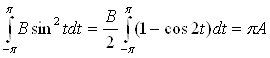 , подставив и выразив В, получаем:
, подставив и выразив В, получаем:
 . (6)
. (6)
Подставим найденные коэффициенты (5) и (6) в уравнение (4):
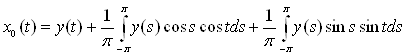
и свернем по формуле:
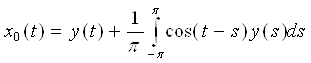
II. Найдем теперь x1(t), для этого необходимо решить следующее уравнение системы (4) §7: А0x1+А1x0 = y1. Так как y1=0 в нашем случае, то мы будем решать уравнение А0x1= – А1x0.

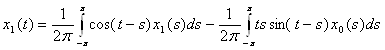
Обозначим 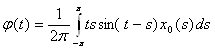 , т.к. мы знаем теперь x0(s), следовательно φ(t) можно вычислить. Имеем:
, т.к. мы знаем теперь x0(s), следовательно φ(t) можно вычислить. Имеем:
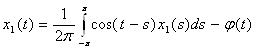
Как в предыдущем случае заменим, ![]() , поэтому
, поэтому ![]()
![]() . (7)
. (7)
где 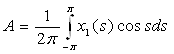 ,
, 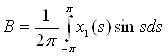 .
.
Умножим уравнение (7) на cos t и проинтегрируем по t от –π до π – получим коэффициент А:

Подсчитав: 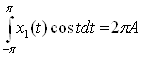 ,
, 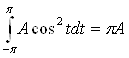 ,
, 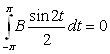 ,
,
имеем  .
.
Аналогично умножив уравнение (7) на sin t и проинтегрируем по t от –π до π – получим коэффициент В: 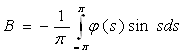 .
.
Составляем функцию x1(t), подставив коэффициенты А и В в уравнение и свернув равенство по формуле косинуса разности:
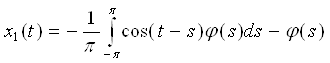 .
.
Таким способом мы можем найти все остальные решения уравнения с любой степенью точности.
Пример 2. Применим метод продолжения по параметру для оценки разрешимости краевой задачи для дифференциального уравнения, а потом решим ее методом малого параметра.
–x'' + b(t)x' +c(t)x = y(t), 0< t <1, (1)
x(0) = x(1) = 0 (2)
Здесь c(t) непрерывна на [0, 1], b(t) непрерывно дифференцируема на [0, 1]. Предположим еще, что на [0, 1] c(t) – b(t)'/2 ≥ α > –8/π (*).
Покажем методом продолжения по параметру, что в этих условиях при всякой правой части y ÎY = С [0, 1] существует единственное решение задачи x Î X = С2 [0, 1] – пространству, состоящему из дважды непрерывно дифференцируемых на [0, 1] функций x(t), удовлетворяющих граничным условиям (2), и с нормой ![]() , где
, где ![]() .
.
Запишем задачу (1) – (2) в операторном виде: Вx = y
Здесь ![]() определен всюду на X со значениями в Y. В качестве оператора А примем
определен всюду на X со значениями в Y. В качестве оператора А примем ![]() ÎL(X, Y).
ÎL(X, Y).
Соединим операторы А и В отрезком
![]() , λ Î [0, 1].
, λ Î [0, 1].
Теперь необходимо установить априорную оценку для решений краевой задачи
–x'' + λb(t)x' + λc(t)x = y(t), 0< t <1, (3)
x(0) = x(1) = 0 (4)
Как только такая оценка будет получена, из теоремы п.8.1. будет следовать однозначная разрешимость краевой задачи (3) – (4).
Умножим уравнение (3) на x(t) и проинтегрируем полученное равенство по t от 0 до 1:
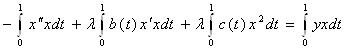 .
.
Заметим, с учетом граничных условий:

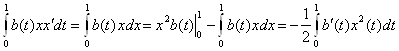
Подставим полученные интегралы и сгруппируем относительно λ:
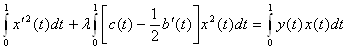 (5)
(5)
Произведем оценку всех трех слагаемых в этом равенстве.
Докажем, что 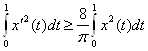 . (6)
. (6)
Заметим, что 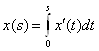 , и значит по неравенству Коши – Буняковского:
, и значит по неравенству Коши – Буняковского:
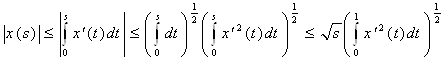 .
.
Точно так же:
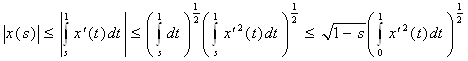 .
.
Перемножим эти неравенства:
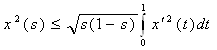 . (6*)
. (6*)
Отсюда, замечая, что 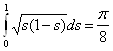 , получим
, получим
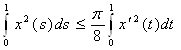
![]()
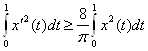 .
.
Далее  (7)
(7)
– это следует из предположения (*).
Последний интеграл равенства (5) можно оценить, используя скалярный квадрат:
![]() , где
, где 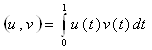 .
.
Для любого ε > 0 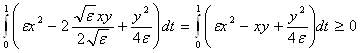
![]()
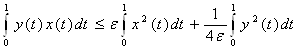 . (8)
. (8)
Используя полученные неравенства (6), (7), (8) и подставляя их в равенство (5), получаем:
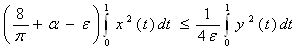 ,
,
считая ε > 0 достаточно малым, имеем
 .
.
Выберем ![]() и получим
и получим
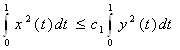 , где
, где ![]() .
.
Возвращаясь снова к равенству (5), получим следующую оценку:
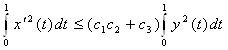 , где
, где ![]() , а
, а ![]() .
.
Теперь с помощью оценки (6*) имеем 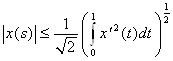 и, значит, учитывая, что
и, значит, учитывая, что 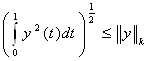 , получим
, получим
![]() (9)
(9)
Из уравнения (3) можем получить оценки для ![]() и
и ![]() :
:
![]() . (10)
. (10)
Здесь ![]() оценивается через
оценивается через ![]() и
и ![]() . Действительно, x(0) = x(1) = 0. по теореме Роля на (0, 1) найдется точка ξ, в которой x'(ξ) = 0. Тогда, запишем уравнение (3) в виде
. Действительно, x(0) = x(1) = 0. по теореме Роля на (0, 1) найдется точка ξ, в которой x'(ξ) = 0. Тогда, запишем уравнение (3) в виде
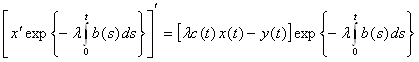 ,
,
(в этом можно убедиться, взяв производную:
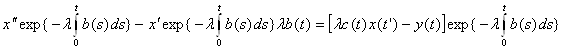
и сократив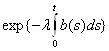 )
)
интегрируем его от ξ до θ и получим
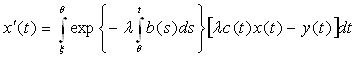 .
.
Отсюда имеем оценку
![]() , (11)
, (11)
где 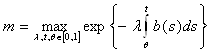 .
.
Теперь подставим полученные результаты в (10):
![]() . (12)
. (12)
Теперь (9), (11) и (12) дают искомую априорную оценку:
![]()
(постоянную с4 нетрудно подсчитать, сложив неравенства(9), (11), (12)и выполнив преобразования).
Таким образом, доказательство разрешимости задачи получено, теперь приступим к ее решению методом малого параметра.
Итак, рассмотрим операторное уравнение:
А(λ)x = y(λ),
где ![]() .
.
I. Начнем с уравнения А0x0 = y (где А0 – коэффициент при нулевой степени λ) системы (4) §7, причем y0 = y, yк = 0, к ≥ 1.
![]()
![]()
![]()
![]()
![]()
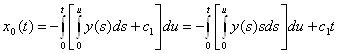 , причем с1 подбирается так, чтобы выполнялось краевое условие: x0(1) = 0.
, причем с1 подбирается так, чтобы выполнялось краевое условие: x0(1) = 0.
II. Найдем x1(t), для этого необходимо решить следующее уравнение: А0x1+А1x0 = y1. Так как y1=0, то мы будем решать уравнение А0x1= – А1x0.
Из того, что ![]() следует следующее уравнение:
следует следующее уравнение:
![]()
![]()
![]()
![]()
![]()

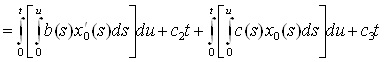 .
.
По аналогии c2 и c3 подбираем так, чтобы выполнялось краевое условие: x0(1) = 0.
Таким образом, решения нашей краевой задачи выглядит так:
![]() ,
,
подставляя найденные решения, имеем:
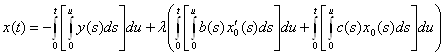
или
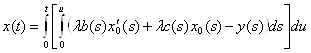
Литература
1. Данфорд Н., Шварц Дж. Линейные операторы. М., 1962
2. Талдыкин А.Т. Элементы прикладного функционального анализа: Учеб. пособие. – М.: Высшая школа, 1982.
3. Треногин В.А. Функциональный анализ. М., 1993.
4. Функциональный анализ./Под. ред. С. Г. Крейна. М., 1972
5. Хатсон В., Пим Дж. С. Приложения функционального анализа и теория операторов. Пер. с англ. – М.: Мир, 1983.
Похожие работы
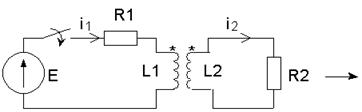
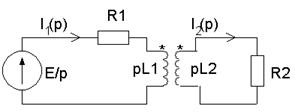
... математических методов, связанных с описанием и анализом типичных явлений, протекающих именно в электротехнических устройствах. 1 Применение преобразования Лапласа и его свойств к расчету переходных процессов Этот метод основан на преобразовании Лапласа. Пусть f(t) – оригинал, а F(p) – изображение этого оригинала по Лапласу. Для сокращения применяют такие обозначения: f(t)F(p), F(p)= Прямое ...
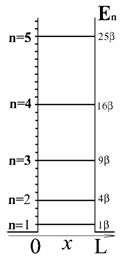
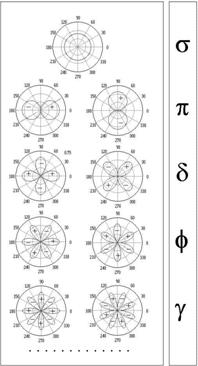
... лишь угловую часть лапласиана и имеет вид: . (6.23) Уравнение Лежандра, встречается в нескольких фундаментальных задачах: 1) в задаче о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) в уравнении Шрёдингера для атома H и водородоподобных ионов. 6.7.3. Уравнение Лежандра это вполне типичное операторное уравнение на
... плотность тока вероятности .(1.9) Из (1.9) следует, что j = 0 для всех функций , у которых функция Ф не зависит от координат. В частности, j= 0 для всех действительных функций . Решения уравнения Шредингера (1.1) в общем случае изображаются комплексными функциями. Использование комплексных функций весьма удобно, хотя и не необходимо. Вместо одной комплексной функции состояние системы можно ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...
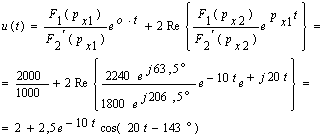


0 комментариев