Навигация
План
I. Вступ
1.1 Фрактал. Історія його виникнення
1.2 Види фракталів та методи їх створення
1.3 Типи самоподібності у фракталах
1.4 Розмірність фракталів
II. Основна частина
2.1 Класифікація алгоритмів створення фракталів
2.2 Системи Ітеріруємих Функцій
2.3 Стиснюючі афінні перетворення
2.4 Метод простої заміни
2.4.1 Серветка Серпінського
2.4.2 Дракон Хартера-Хейтуея
2.5 Алгебраїчні фрактали
2.6 Графіки функцій комплексної змінної
2.7 Формули побудови фракталів
2.7.1 Різновид алгебраїчних фракталів — басейни Ньютона
2.7.2 Множина Жюліа та Мандельброта
III. Висновок
IV. Використана література
І Вступ
1.1 Фрактал. Історія його виникнення
Все, що створено людиною, обмежено площинами. Коли зустрічається об’єкт у природі, то спочатку можна побачити, що описати його форму можна лише наближено й допоможуть в цьому фрактали. Де закінчуються правильні форми Евклідової геометрії, там зустрічаються фрактали.
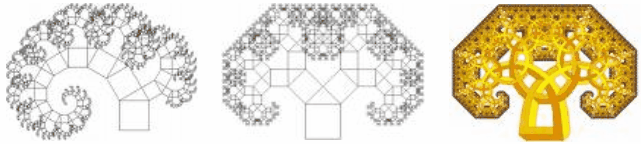
Фракта́л (лат. fractus — подрібнений, дробовий) – нерегулярна, самоподібна структура. У широкому розумінні фрактал означає фігуру, малі частини якої в довільному збільшенні є подібними до неї самої (мал.1).
Об'єкти, які тепер називаються фракталами, досліджувались задовго до того, як їм було дано таку назву. В етноматематиці, наприклад в роботах Рона Еглаша "Африканські Фрактали", задокументовано поширені фрактальні геометричні фігури в мистецтві тубільців. У 1525 році німецький митець Альбрехт Дюрер опублікував свою працю “Керівництво Художника”, один із розділів якої має назву "Черепичні шаблони, утворені пентагонами". Пентагон Дюрера багато в чому є схожим на килим Серпінського, але замість квадратів використовуються п'ятикутники. Джексон Поллок (американський експресіоніст 50-тих років) малював об'єкти, дуже схожі на фрактали.
Ідею "рекурсивної самоподібності" було висунуто філософом Лейбніцом, який також розробив багато з деталей цієї ідеї. У 1872 Карл Веєрштрасс знайшов приклад функції з неінтуітивною особливістю, скрізь неперервної, але ніде недиференційованої — графік цієї функції тепер називався б фракталом. У 1904 Хельга Фон Кох, незадоволений занадто абстрактним та аналітичним означенням Веєрштрасса, розробив більш геометричне означення схожої функції, яка тепер має назву сніжинки Коха. Ідею самоподібних кривих, котрі складаються із частин, схожих на ціле, було далі розвинено Полем П'єром Леві, який у своїй роботі "Криві та поверхні на площині та у просторі", виданій 1938 року, описав нову фрактальну криву, відому тепер як Крива Леві (мал.2 а, б, в).
а) б) в)
Мал.2
Ґеорг Кантор навів приклади підмножин дійсних чисел із незвичними властивостями — ці множини Кантора тепер також визнаються як фрактали.
Ітераційні функції на комплексній площині досліджувались в кінці XIX та на початку XX століття Анрі Пуанкаре, Феліксом Кляйном, П'єром Фату та Ґастоном Жюліа. Проте за браком сучасної комп'ютерної графіки у них забракло засобів відобразити красу багатьох із відкритих ними об'єктів.
У 1975 році Мандельброт використав слово фрактал як назву для об'єктів, розмірність Хаусдорфа яких є більшою за топологічну розмірність, наприклад Крива Хильберта (мал.3 а,б,в,г).
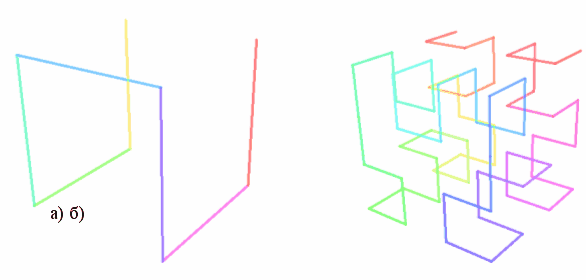

Мал.3
1.2 Види фракталів та методи їх створення
Існують три поширені методи створення (генерування) фракталів:
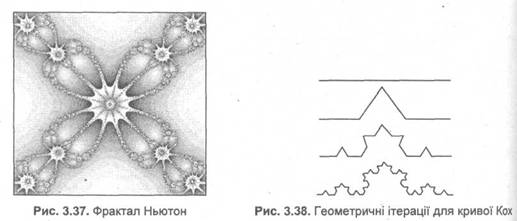
Перший метод — ітераційні функції, які будуються відповідно до фіксованого правила геометричних заміщень, в результаті яких утворюються геометричні фрактали, наприклад: сніжинка Коха (мал.4).
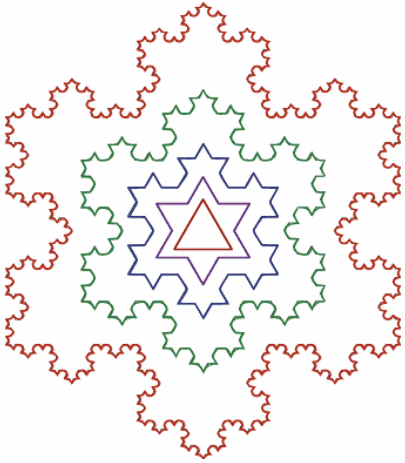
Мал.4
А також множина Кантора, килим Серпінського, трикутник Серпінського, крива Пєано, крива Коха, крива дракона, Т-Квадрат та губка Менгера є прикладами геометричних фракталів.
Другий метод — рекурентні відношення, це фрактали, що визначаються рекурентним відношенням у кожній точці простору (такому як площина комплексних чисел). Отримані таким методом фрактали називають алгебраїчними.
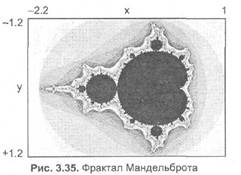
Прикладами алгебраїчних фракталів є множина Мандельброта (мал.5), палаючий корабель та фрактал Ляпунова.

Мал.5
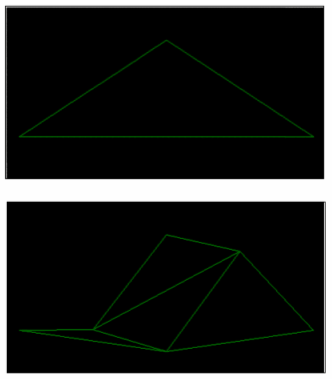
Третій метод — випадкові процеси, це фрактали, що генеруються з використанням стохастичних, а не детермінованих процесів, наприклад: фрактальні ландшафти (мал.6 а,б,в,г,д), траєкторія Леві та броунівське дерево.
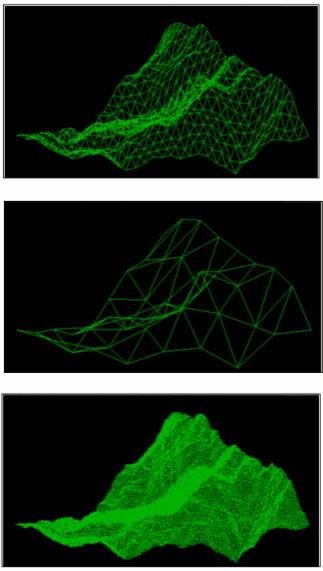
Мал.6.
Похожие работы
... новий термін і назвімо таку єдність сакрохронотопом) - фундаментальний, первинний релігійний прадосвід людини релігійної. Пошук виявів sacrum'y в художній літературі здійснюється через інтерпретаційно-герменевтичні окреслення характеристик сакрального часу та священного простору (сакрохронотопу), виявлення ієрофаній, теофаній, через аналіз структурних компонентів релігійної символіки, в описі ...
... ів: при утраті деяких кадрів; при перегляді фільму не з початку; при необхідності в цілях синхронізації пропускати декілька нерозпакованих кадрів (на повільних процесорах). Розглянемо деякі формати мультимедіа. • Формат AVI (Audio Video Interleaved), що є спеціальним форматом представлення відеофайлів в операційних системах сімейства Windows і тому широко використовується на персональних комп' ...
... груп тіла людини, як дуже складного інформаційного комплексу, завжди пов'язана з присутністю взаємного інформаційного обміну і взаємодії з навколишнім середовищем. І, якщо з будь-якої причини, система взаємного інформаційного обміну, яка забезпечує стабільність і оптимальність внутрішньоструктурних взаємних зв'язків, торкнеться, виникає дисбаланс, який призводить до того, що одні системи різко пі ...
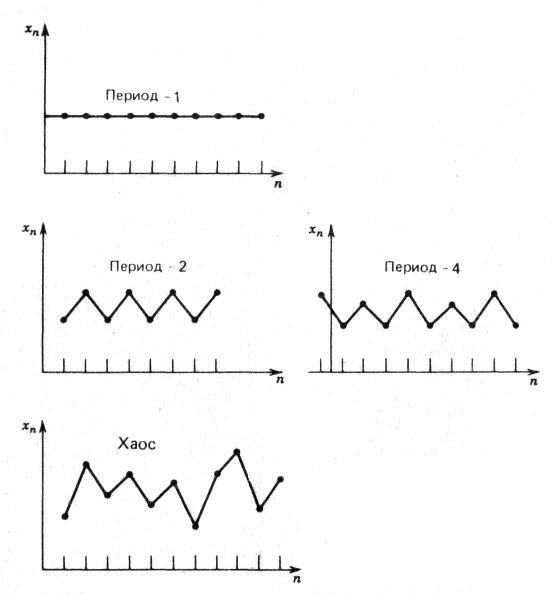
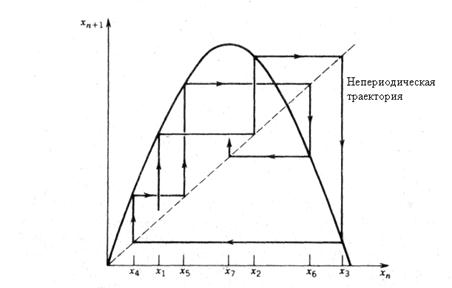
кационного параметра називають універсальною властивістю певних класів одновимірних різницевих моделей динамічних процесів. Подвоєння періоду і відношення Фейгенбаума (1.4) виявляються в багатьох фізичних експериментах. Це означає, що в багатьох безперервних еволюційних процесах зведення до різницевого рівняння за допомогою перетину Пумнкаре приводить до квадратичного відображення (1.1); звідси ...


0 комментариев