Навигация
Системи Ітеріруємих Функцій
23784
знака
0
таблиц
23
изображения
2.2 Системи Ітеріруємих Функцій
У евклідовом просторі 
відстань 
(x;y) між точками x=(
;
) і y=(
;
) визначається за допомогою наступної формули
Відстань в просторі можна також вимірювати функцією 
(x;y)=|
-
|+|
-
|.
Дві приведені функції, будучи вимірами відстані, по-різному визначають відстані між двома точками. Існують чотири основні властивості функції відстані:
ü відстані від точки x до точки y і від точки y до точки x рівні: d(x;y)=d(у;x);
ü відстань від точки x до цієї ж точки x дорівнює нулю: d(x;x)=0;
ü відстань по прямій - це найкоротша відстань між двома точками: d(x;y) <=d(x;z)+d(z;y);
ü для двох точок x і у функція відстані має бути дійсною, скінченою і додатною : 
.
Функція відстані, що задовольняє даним властивостям, називається метрика.
Метричний простір (X,d) - множина точок X разом з метрикою d, визначеною на X.
Перетворення - зіставлення, згідно заздалегідь визначеному правилу, точці в одному просторі точки в іншому (можливо і в тому ж самому просторі).
Відображення, це перетворення, яке переводить простір X1 в простір X2 і позначається fn: X1 X2.
Стиснююче відображення - перетворення в метричному просторі X1 X2 за умови існування коефіцієнта стиснення перетворення f: 0
s<1 такого, що d(f(x1),f(x2)) sd(x1,x2) для всіх 
Система ітеріруємих функцій (Iterated Function System) складається з повного метричного простору (X,d) і скінченної множини стиснюючих відображень fn: X1 X2 з коефіцієнтами стиснення Sn.
2.3 Стиснюючі афінні перетворення
Мал. 8.
Перш ніж розкривати зміст поняття - стиснюючі афінні перетворення, розглянемо лінійне перетворення 
на комплексній площині Z, яке переводить рівносторонній трикутник з довжиною сторони рівній одиниці в рівносторонній трикутник в два рази меншого розміру представлений на мал. 8.
Розглянуте вище лінійне перетворення на комплексній площині є окремим випадком афінного перетворення площини
xn+1=axn+byn+e
yn+1=cxn+dyn+f
Його можна подати в матричному вигляді
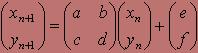
Так, наприклад, розглянуте перетворення можна записати у вигляді
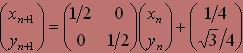
У загальному випадку афінне перетворення на площині задається шістьма незалежними дійсними числами. Два числа e і f описують звичайну трансляцію, а чотири числа а, b, с, d задають довільне лінійне перетворення при незмінному положенні початку координат (0;0).
Похожие работы
... новий термін і назвімо таку єдність сакрохронотопом) - фундаментальний, первинний релігійний прадосвід людини релігійної. Пошук виявів sacrum'y в художній літературі здійснюється через інтерпретаційно-герменевтичні окреслення характеристик сакрального часу та священного простору (сакрохронотопу), виявлення ієрофаній, теофаній, через аналіз структурних компонентів релігійної символіки, в описі ...
... ів: при утраті деяких кадрів; при перегляді фільму не з початку; при необхідності в цілях синхронізації пропускати декілька нерозпакованих кадрів (на повільних процесорах). Розглянемо деякі формати мультимедіа. • Формат AVI (Audio Video Interleaved), що є спеціальним форматом представлення відеофайлів в операційних системах сімейства Windows і тому широко використовується на персональних комп' ...
... груп тіла людини, як дуже складного інформаційного комплексу, завжди пов'язана з присутністю взаємного інформаційного обміну і взаємодії з навколишнім середовищем. І, якщо з будь-якої причини, система взаємного інформаційного обміну, яка забезпечує стабільність і оптимальність внутрішньоструктурних взаємних зв'язків, торкнеться, виникає дисбаланс, який призводить до того, що одні системи різко пі ...
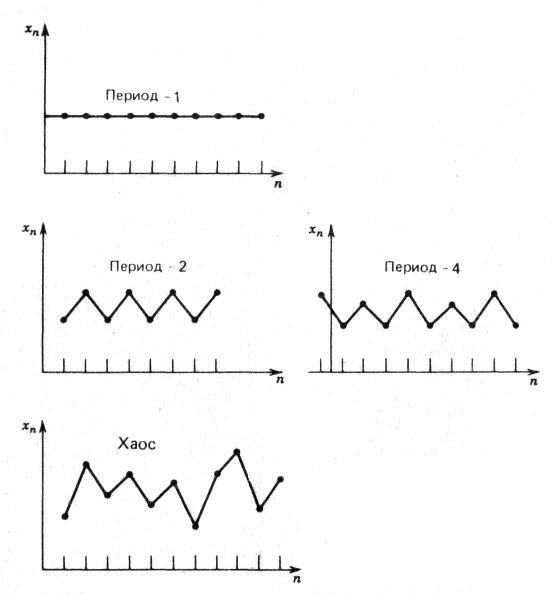
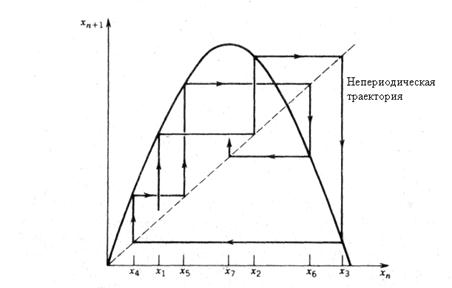
кационного параметра називають універсальною властивістю певних класів одновимірних різницевих моделей динамічних процесів. Подвоєння періоду і відношення Фейгенбаума (1.4) виявляються в багатьох фізичних експериментах. Це означає, що в багатьох безперервних еволюційних процесах зведення до різницевого рівняння за допомогою перетину Пумнкаре приводить до квадратичного відображення (1.1); звідси ...
0 комментариев