Навигация
Типи самоподібності у фракталах
1.3 Типи самоподібності у фракталах
Розрізняють три типи самоподібності у фракталах:
Точна самоподібність — це найсильніший тип самоподібності; фрактал виглядає однаково при різних збільшеннях. У фракталів, згенерованих з використанням ітераційних функцій, часто виявляється точна самоподібність.
Майже самоподібність — слабка форма самоподібності; фрактал виглядає приблизно (але не точно) самоподібним при різних збільшеннях. Майже самоподібні фрактали містять малі копії цілого фракталу у перекручених та вироджених формах. Фрактали, згенеровані з використанням рекурентних відношень, зазвичай є майже (але не точно) самоподібними.
Статистична самоподібність — це найслабкіша форма самоподібності; фрактал має чисельні або статистичні міри, що зберігаються при збільшенні. Найприйнятніші означення "фракталів" просто містять в собі деякий вид статистичної самоподібності (розмірність фракталу, саме по собі, є чисельною мірою, що зберігається при збільшенні). Ймовірнісні фрактали є прикладами фракталів, які є статистично, але не майже й не точно самоподібними.
1.4 Розмірність фракталів
У евклідової геометрії є поняття розмірності: розмірність крапки — нуль, відрізка та кола — одиниця, круга і сфери — два, кулі — три. З одновимірними об'єктами ми пов'язуємо поняття довжини, з двовимірними - площі і так далі. Але як можна уявити собі множину з розмірністю 3/2? Мабуть, для цього потрібно щось проміжне між довжиною і площею, і якщо довжину умовно назвати 1-мірою, а площа - 2-мірою, то потрібна (3/2) -міра.
У 1919 році Ф. Хаусдорф дійсно визначив таку а-міру і на цій основі кожній множині в евклідовому просторі підставив число, назване їм метричною розмірністю. Він же навів перші приклади множин з дробовою розмірністю. Виявилось, що дробову розмірність мають канторова множина, крива Коха і інші екзотичні об'єкти, до недавнього часу маловідомі за межами математики.
Оскільки фрактал складається з нескінченного числа елементів, що повторюються, неможливо точно виміряти його довжину. Це означає, що чим точнішим інструментом ми будемо його вимірювати, тим більшою виявиться його довжина. Тоді як гладка евклідова лінія заповнює в точності одновимірний простір, фрактальна лінія виходить за межі одновимірного простору, вторгаючись у двовимірне. Таким чином, фрактальна розмірність кривої Коха знаходитиметься між 1 і 2. Найдивовижнішим виявляється те, що й багато природних об'єктів володіють ніби дробовою розмірністю, хоча, відверто кажучи, для природних об'єктів таку розмірність обчислити неможливо. Правильніше сказати, що в певних діапазонах спостереження природні об'єкти, що виникли в результаті довгої дифузії й абсорбції, схожі на фрактальні множини. Наприклад, розмірність побережжя лежить між 1,01 і 1,6, а кровоносної системи людини — між 3,4 і 3,6
ІІ Основна частина
2.1 Класифікація алгоритмів створення фракталів
Бенуа Мандельброт в своїх книгах навів яскраві приклади вживання фракталів до пояснення деяких природних явищ. Мандельброт приділив велику увагу цікавій властивості, якою володіють багато фракталів. Річ у тому, що часто фрактал можна розбити на скільки завгодно малі частини так, що кожна частина виявиться просто зменшеною копією цілого. Інакше кажучи, якщо ми дивитимемося на фрактал в мікроскоп, то із здивуванням побачимо ту ж саму картину, що і без мікроскопа. Це властивість самоподібності різко відрізняє фрактали від об'єктів класичної геометрії.
Необхідно відзначити, що властивість самоподiбностi характерна лише для регулярних фракталів.Багато регулярних фракталів будуються шляхом нескiнченного повторення декількох простих операцій - заміною одного елементу деякою комбінацією інших, йому подібних. Потім ця ж операція повторюється з кожним з цих елементів, і так далі до нескінченності. На методі простої заміни заснований перший алгоритм побудови фракталів.
Виникає питання, чи не можна цю "процедуру заміни" перекласти мовою математичних формул. Таким чином, в середині 80-х років з'явився метод Систем Ітеріруємих Функцій - СІФ (Iterated Function System - IFS) як простий засіб здобуття фрактальних структур. Таким чином, деякі з вищеперелічених фракталів можна отримати за допомогою методу СІФ. Метод Систем Ітеріруємих функцій є основою для другого алгоритму побудови фрактальних структур. Замість детермінованого способу побудови регулярних фракталів в алгоритм створення фрактальних структур був включений деякий елемент випадковості, що приводить до побудови випадкових фракталів. Багато фракталів можуть бути отримані за допомогою цих двох алгоритмів. Тоді в першому випадку вони побудовані як регулярні фрактали, а в другому як випадкові.
Одним з найбільш яскравих прикладів серед різних систем ітеріруємих функцій є відкрита система М. Бранслі з чотирьох стискуючих афінних перетворень, аттрактором для якої є множина точок, яка дуже нагадує по формі зображення листа папороті.
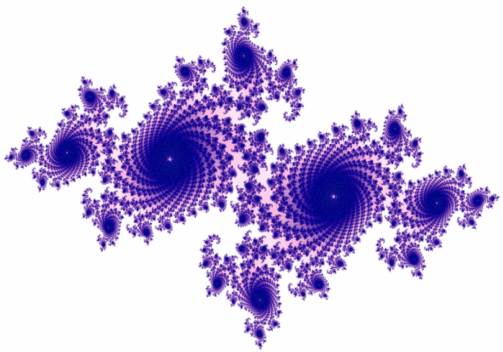
Мал.7
Третім алгоритмом створення фрактальних об'єктів на площині є використання комплексних відображень, що зіставляють одному комплексному числу інше комплексне число за деяким ітераційним правилом. Прикладом фрактала отриманого за допомогою комплексних відображень є множина Жюліа (мал.7).
Похожие работы
... новий термін і назвімо таку єдність сакрохронотопом) - фундаментальний, первинний релігійний прадосвід людини релігійної. Пошук виявів sacrum'y в художній літературі здійснюється через інтерпретаційно-герменевтичні окреслення характеристик сакрального часу та священного простору (сакрохронотопу), виявлення ієрофаній, теофаній, через аналіз структурних компонентів релігійної символіки, в описі ...
... ів: при утраті деяких кадрів; при перегляді фільму не з початку; при необхідності в цілях синхронізації пропускати декілька нерозпакованих кадрів (на повільних процесорах). Розглянемо деякі формати мультимедіа. • Формат AVI (Audio Video Interleaved), що є спеціальним форматом представлення відеофайлів в операційних системах сімейства Windows і тому широко використовується на персональних комп' ...
... груп тіла людини, як дуже складного інформаційного комплексу, завжди пов'язана з присутністю взаємного інформаційного обміну і взаємодії з навколишнім середовищем. І, якщо з будь-якої причини, система взаємного інформаційного обміну, яка забезпечує стабільність і оптимальність внутрішньоструктурних взаємних зв'язків, торкнеться, виникає дисбаланс, який призводить до того, що одні системи різко пі ...
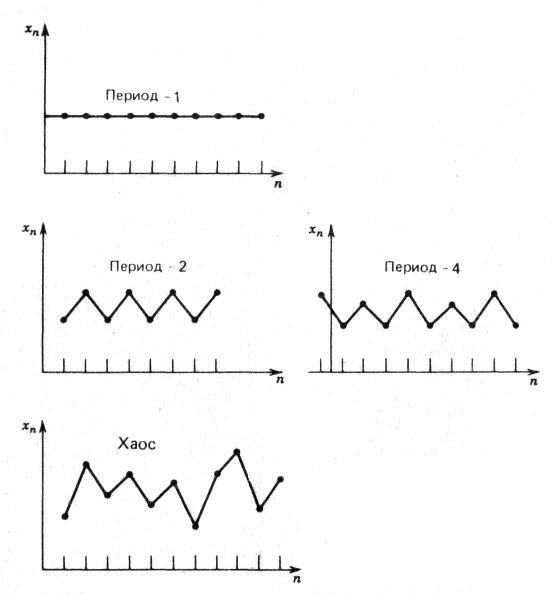
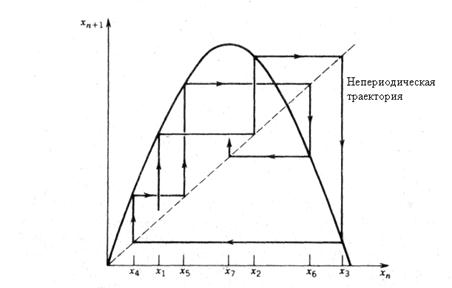
кационного параметра називають універсальною властивістю певних класів одновимірних різницевих моделей динамічних процесів. Подвоєння періоду і відношення Фейгенбаума (1.4) виявляються в багатьох фізичних експериментах. Це означає, що в багатьох безперервних еволюційних процесах зведення до різницевого рівняння за допомогою перетину Пумнкаре приводить до квадратичного відображення (1.1); звідси ...


0 комментариев