Навигация
2.4 Метод простої заміни
2.4.1 Серветка Серпінського
Фрактал серветка Серпінського може бути побудований як за допомогою методу простої заміни, який застосовують для побудови регулярних фракталів, так і за допомогою методу IFS.
Розглянемо алгоритм побудови, заснований на методі простої заміни. Правильний трикутник ділений середніми лініями на чотири рівні трикутники і внутрішність центрального викидаємо. З трьома трикутниками, що залишилися, робимо те ж саме і так нескінченне число разів. Після певного числа викидань залишається множина S, представлена на мал. 9, яка є серветкою Серпінського.

Мал.9.
Фрактальна розмірність серветки Серпінського підраховується по формулі D=ln3/ln2=1,5849. Серветка має нульову площу, оскільки неважко перевірити, що в процесі її побудови була виключена площа, в точності рівна площі вихідного трикутника. Про це ж свідчить і значення фрактальної розмірності D<2, яка менше розмірності площини, на якій знаходиться цей об'єкт.
Всім відомий трикутник Паскаля (мал.10) за допомогою якого обчислюють коефіцієнти розкладу виразу виду ![]() . Починаючи з трикутника, що складається з одиниць, обчислюють значення на кожному наступному рівні шляхом додавання сусідніх чисел; останньою ставлять одиницю.
. Починаючи з трикутника, що складається з одиниць, обчислюють значення на кожному наступному рівні шляхом додавання сусідніх чисел; останньою ставлять одиницю.

Мал.10
Таким чином можна наприклад визначити, що:
![]() .
.
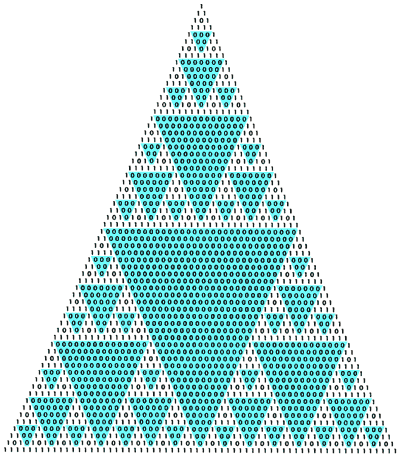
Мал.11
Цей трикутник можна перетворити на привабливий фрактальний візерунок (мал.11), якщо замінити непарні коефіцієнти одиницями, а парні — нулями.
Візерунок демонструє властивості коефіцієнтів, що використовується при «арифметизації» комп’ютерних програм, що перетворює їх в алгебраїчні рівняння.
2.4.2 Дракон Хартера-Хейтуея
Для більшості регулярних фракталів фрактальна розмірність D менша, ніж розмірність d того простору, в якому знаходиться даний фрактальний об'єкт. Нерівність D < d відображає факт некомпактності фрактала, причому чим більше розрізняються величини D і d, тим більше рихлим є фрактал. Існують фрактали, які щільно заповнюють простір, в якому вони знаходяться, так що їх фрактальна розмірність D = d. Одним з прикладів такого роду є криві Пеано (Peano curves). Дракон Хартера-Хейтуея (мал.12) є прикладом кривої Пеано, для якої область, яку вона заповнює на площині, має химерну форму.

Мал.12
Перші чотири кроки його побудови представлено на мал.12
Як випливає з мал.13 кожний з відрізків прямої на наступному кроці замінюється на два відрізки, створюючих бічні сторони рівнобедреного прямокутного трикутника, для якого вихідний відрізок був би гіпотенузою. В результаті відрізок як би прогинається під прямим кутом. Напрям прогину чергується. Перший відрізок прогинається вправо (по ходу руху зліва направо), другий - вліво, третій - знову управо і так далі На мал.13 пунктиром показана конфігурація попереднього кроку. Таким чином, після кожного кроку число наявних відрізків подвоюється, а довжина кожного відповідно зменшується вдвічі. Тому фрактальна розмірність кривої, що утворюється в результаті (після нескінченного числа кроків), рівна 2.
Для реалізації вказаного вище алгоритму побудови необхідно перейти до комплексних чисел ZA, ZB и ZC (Мал.14).
Мал.13
Для знаходження координат точки C представимо комплексні числа в тригонометричній формі. Знаходження координат точки C представлене формулами 1-8.
![]() (1)
(1)
![]() (2)
(2)
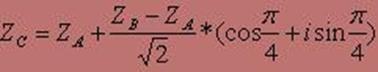 (3)
(3)
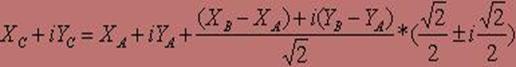 (4)
(4)
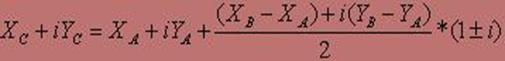 (5)
(5)
![]() (6)
(6)
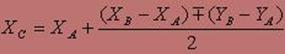
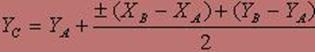
Гранична фрактальна крива (коли n прямує до нескінченності) називається драконом Хартера-Хейтуея. У машинній графіці використання геометричних фракталів необхідно для отримання зображень дерев, кущів, берегових ліній. Двовимірні геометричні фрактали використовуються для створення об’ємних текстур (малюнка на поверхні об’єкту).
2.5 Алгебраїчні фракталиЦе найкрупніша група фракталів. Отримують їх за допомогою нелінійних процесів в n-мірних просторах. Найбільш досліджені двомірні процеси. Інтерпретуючи нелінійний ітераційний процес, як дискретну динамічну систему, можна користуватися термінологією теорії цих систем: фазовий портрет, сталий процес, аттрактор та інші.
Відомо, що нелінійні динамічні системи володіють декількома стійкими станами. Той стан, в якому виявилася динамічна система після деякої кількості ітерацій, залежить від її початкового стану. Тому кожен стійкий стан (або як говорять - аттрактор) володіє деякою областю початкових станів, з яких система обов'язково попаде в дані кінцеві стани. Таким чином фазовий простір системи розбивається на області тяжіння аттракторів. Якщо фазовим є двомірний простір, то забарвлюючи області тяжіння різними кольорами, можна отримати кольоровий фазовий портрет цієї системи (ітераційного процесу). Змінюючи алгоритм вибору кольору, можна отримати складні фрактальні картини з химерними багатокольоровими узорами. Несподіванкою для математиків стала можливість за допомогою примітивних алгоритмів породжувати дуже складні нетривіальні структури.

Мал.14.
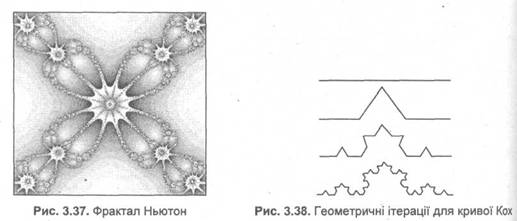
Наприклад, фрактал Ньютона, який штрихується відповідно до кількості ітерацій (мал.14).
Похожие работы
... новий термін і назвімо таку єдність сакрохронотопом) - фундаментальний, первинний релігійний прадосвід людини релігійної. Пошук виявів sacrum'y в художній літературі здійснюється через інтерпретаційно-герменевтичні окреслення характеристик сакрального часу та священного простору (сакрохронотопу), виявлення ієрофаній, теофаній, через аналіз структурних компонентів релігійної символіки, в описі ...
... ів: при утраті деяких кадрів; при перегляді фільму не з початку; при необхідності в цілях синхронізації пропускати декілька нерозпакованих кадрів (на повільних процесорах). Розглянемо деякі формати мультимедіа. • Формат AVI (Audio Video Interleaved), що є спеціальним форматом представлення відеофайлів в операційних системах сімейства Windows і тому широко використовується на персональних комп' ...
... груп тіла людини, як дуже складного інформаційного комплексу, завжди пов'язана з присутністю взаємного інформаційного обміну і взаємодії з навколишнім середовищем. І, якщо з будь-якої причини, система взаємного інформаційного обміну, яка забезпечує стабільність і оптимальність внутрішньоструктурних взаємних зв'язків, торкнеться, виникає дисбаланс, який призводить до того, що одні системи різко пі ...
кационного параметра називають універсальною властивістю певних класів одновимірних різницевих моделей динамічних процесів. Подвоєння періоду і відношення Фейгенбаума (1.4) виявляються в багатьох фізичних експериментах. Це означає, що в багатьох безперервних еволюційних процесах зведення до різницевого рівняння за допомогою перетину Пумнкаре приводить до квадратичного відображення (1.1); звідси ...


0 комментариев