Ребро куба равно а

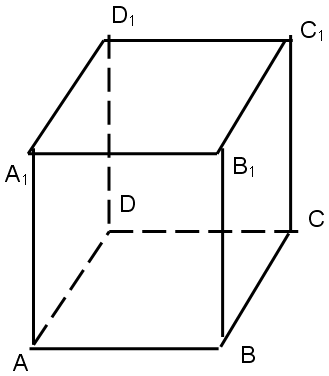
1. Ребро куба равно а.

Найдите:

Диагональ грани: d= a√2.

Диагональ куба: D= a√3.

Периметр основания: P= 4a.

 

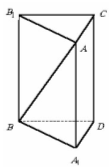
2. Основанием прямой призмы является равнобедренный треугольник, в котором высота проведенная к основанию равняется 8см. Высота призмы равняется 12см. Найдите полною поверхность призмы если боковая грань что содержит основание треугольника - квадрат.

Решение

Площадь поверхности призмы будет равна сумме площадей оснований и сумме площадей боковых поверхностей, то есть , где - площадь основания призмы, - площадь боковой поверхности, содержащей основание, - площадь боковой поверхности, содержащей стороны равнобедренного треугольника. (Они равны, так как стороны основания равны в следствие того, что треугольник равнобедренный, а вторые стороны равны высоте призмы)

Поскольку боковая грань, содержащая основание треугольника, является квадратом, то основание треугольника также равно 12 см. (основание треугольника одновременно является стороной грани).

Таким образом, зная высоту и основание равнобедренного треугольника можно найти его остальные стороны и площадь:

Катеты, соответственно равны (у нас высота, являющаяся в равнобедренном треугольнике одновременно и медианой , с каждым из катетов образует прямоугольный треугольник) по теореме Пифагора:

Таким образом:

,

3. В правильной четырёхугольной призме площадь основания 144 , а высота 14 см. Найти диагональ призмы.

Решение

Правильный четырехугольник – это квадрат.

Соответственно, сторона основания будет равна

Откуда диагональ основания правильной прямоугольной призмы будет равна

Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:

Ответ: 22 см

4. Рассмотрим правильную четырехугольную призму , диагональное сечение которой – квадрат. Через вершину  и середины ребер АВ и ВС проведена плоскость. Найти площадь полученного сечения, если

Решение

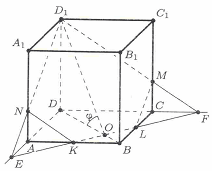
Построение сечения видно на рисунке, где К и L – середины сторон АВ и ВС основания призмы, Е и F – точки пересечения прямой КL соответственно с продолжениями сторон DA и DC. Сечением является пятиугольник  площадь которого можно найти. Можносначала вычислить площади треугольников  и  а потом от площади первого треугольника вычесть удвоенную площадь второго (поскольку треугольники  и  равны). Однако в данном случае проще воспользоваться формулой:

Проекция пятиугольника  на плоскость основания призмы есть пятиугольник , площадь которого найдем, вычитая из площади квадрата  площадь треугольника ВКL:

Пусть диагональ ВD основания пересекает отрезок КL в точке О. Так как  и  (согласно теореме о трех перпендикулярах), то  – линейный угол двугранного угла КL.

Далее находим:

 

Из прямоугольного треугольника  по теореме Пифагора имеем:

Значит,  и

5. Дана правильная призма: , . Найти высоту призмы.

Решение

Площадь основания

АВ= 2 см.

Периметр основания Р = 8 см.

Высота призмы

6. Основанием параллелепипеда служит квадрат. Одна из вершин верхнего основания равноудалена от всех вершин нижнего основания и находится на расстоянии b от этого основания. Сторона основания равна a . Найдите полную поверхность параллелепипеда.

Решение

Пусть  – данный параллелепипед с основаниями ,  и боковыми рёбрами , причём ABCD – квадрат со стороной a , вершина  равноудалена от вершин A, B, C и D, а расстояние от вершины  до плоскости основания ABCD равно b. Поскольку точка  равноудалена от вершин квадрата ABCD, она лежит на перпендикуляре к плоскости ABCD, проходящем через центр O квадрата. Перпендикуляр, опущенный из точки O на сторону BC, проходит через её середину M. По теореме о трёх перпендикулярах , поэтому  – высота грани . Из прямоугольного треугольника  находим, что

.

Значит,

Аналогично,

Если S – полная поверхность параллелепипеда , то

.

7. Докажите, что если сечение параллелепипеда плоскостью является многоугольником с числом сторон, большим трёх, то у этого многоугольника есть параллельные стороны.

Доказательство

У параллелепипеда 3 пары параллельных граней. Если плоскость пересекает более трёх граней, то по крайней мере две стороны многоугольника сечения лежат в противоположных гранях параллелепипеда. По теореме о пересечении двух параллельных плоскостей третьей эти две стороны параллельны.

8. В параллелепипеде  грань ABCD – квадрат со стороной 5, ребро  также равно 5, и это ребро образует с рёбрами AB и AD углы . Найдите диагональ .

Решение

Треугольник – равносторонний, т.к.  = AB и . Поэтому . Аналогично, . Боковые рёбра  треугольной пирамиды  с вершиной  равны между собой, значит, высота  этой пирамиды проходит через центр окружности, описанной около основания ABD , а т.к. треугольник ABD прямоугольный, то точка O – середина его гипотенузы BD, т.е. центр квадрата ABCD. Из прямоугольного треугольника  находим, что

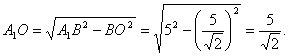
Поскольку , точка  равноудалена от вершин C и D, поэтому её ортогональная проекция K на плоскость основания ABCD также равноудалена от C и D, а значит, лежит на серединном перпендикуляре к отрезку CD. Поскольку || и =, четырёхугольник  – прямоугольник, поэтому OK==5. Продолжим отрезок KO до пересечения с отрезком AB в точке M. Тогда M – середина AB и MK=MO+OK=. Из прямоугольных треугольников MKB и  находим, что:

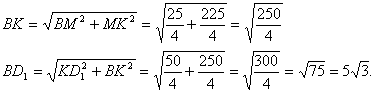
9. На ребре AD и диагонали  параллелепипеда  взяты соответственно точки M и N, причём прямая MN параллельна плоскости  и AM:AD = 1:5. Найдите отношение .

Решение

Пусть P – центр параллелограмма ABCD. Плоскости  и  пересекаются по прямой , поэтому прямые  и  пересекаются в некоторой точке Q, причём

По теореме о пересечении двух параллельных плоскостей третьей плоскости α и  пересекаются по прямой, проходящей через точку E параллельно . Ясно, что точка пересечения этой прямой с прямой  и есть точка N (прямая MN лежит в плоскости, параллельной плоскости ). Рассмотрим параллелограмм . Так как

 то

10. Три отрезка, не лежащие в одной плоскости, имеют общую точку и делятся этой точкой пополам. Докажите, что концы этих отрезков служат вершинами параллелепипеда.

Решение

Пусть O – общая середина отрезков ,  и . Тогда AB||и AD||. Значит, плоскости ABD и  параллельны. Аналогично, плоскость  параллельна плоскости . В плоскостях ABD и  возьмём соответственно точки C и  так, что ABCD и  – параллелограммы. Так как CD||AB , AB|| и ||, то CD||. Поэтому плоскости  и  также параллельны. Шестигранник , образован пересечением трёх пар параллельных плоскостей. Следовательно, это параллелепипед.

Тесты