Методика проведения корреляционного анализа

 2.2. Методика проведения корреляционного анализа

Проводится в несколько этапов. На первом этапе необходимо составить выборку фактических данных о значении фактора и соответствующих значений анализируемого показателя. Чем больше исходных данных, тем точнее будут результаты расчетов. Минимальное количество наблюдений – 8, оптимальное – около 30. Результаты наблюдения ранжируются в порядке увеличения показателя-фактора. Затем рассчитываются среднеквадратичные и нормированные отклонения. Обозначим анализируемый показатель У, показатель - фактор Х.

Среднеквадратичные отклонения:

sх = (∑ ( х_i– x_ср))/ n,

sу = (∑ ( y_i– y_ср))/ n,

где n – количество наблюдений;

x_ср , y_ср - среднеарифметические значения соответственно х и у.

Нормированные отклонения:

Тх = ( х_i– x_ср)/ sх;

Ту = ( y_i– y_ср)/ sу.

Коэффициент корреляции:

R = (S Тх * Ту) / n.

По значению коэффициента корреляции определяют тесноту и характер взаимосвязи между показателями. Коэффициент может изменяться в диапазоне от 0 до 1 и может иметь как положительное, так и отрицательное значение. Чем ближе абсолютное значение коэффициента к единице, тем более тесная взаимосвязь между показателями. Положительное значение говорит о прямой взаимосвязи, отрицательное – об обратной. Пороговое значение коэффициента для осуществления дальнейших расчетов – 0,7.

При значении 0,7 индекс детерминации, который равен квадрату коэффициента корреляции, имеет значение 0,49. Индекс детерминации показывает долю влияния выбранного фактора на анализируемый показатель. Очевидно, что если доля влияния выбранного фактора меньше 0,5, дальнейшие расчеты не имеют смысла.

После оценки тесноты взаимосвязи необходимо выбрать функцию, график которой максимально приближенно описывает данную взаимосвязь. Наиболее часто используются графики следующих функций:

У = А + В * Х;

У = А + В * ln X;

У = А + В / Х.

После выбора функции необходимо рассчитать параметры уравнения А и В. Используется метод наименьших квадратов. Решение сводится к решению системы линейных уравнений. Приведен пример системы линейных уравнений для линейной функции:

n * a + b * ∑x = ∑y;

a * ∑x + b * ∑x² = ∑(x*y).

После определения параметров модель можно использовать. Для этого подставляем в формулу желаемое значение фактора и определяем вероятное значение показателя. В качестве проверки можно рассчитать ошибку аппроксимации – процент отклонения значения фактического от значения, рассчитанного по модели:

Ап = ( 1 / n) * ( |У ф – У р| )* 100 / У ф.

Значение ошибки аппроксимации до 10% говорит о наилучшем подборе модели.

Метод экстраполяции временных рядов заключается в определении тенденции изменения показателя во времени. Может считаться частным случаем корреляционного анализа, когда в качестве фактора выступает время. Однако экстраполяция применяется и тогда, когда изменение показателя зависит от нескольких факторов, и его трудно описать однофакторной функцией. В этом случае определение тенденции изменения показателя может быть единственным возможным способом прогнозирования (рис. 2.1) [4, c.35].

Рис. 2.1. Пример экстраполяции показателя

3. МЕТОДЫ ОПТИМИЗАЦИИ В ЭКОНОМИЧЕСКОМ АНАЛИЗЕ

Основа всех приемов оптимизации – нахождение экстремума функции при заданных ограничениях. Например, нахождение максимума прибыли при ограничении по загруженности производственной мощности.

3.1. Использование графических методов в экономическом анализе

Графические методы связаны прежде всего с геометрическим изображением функциональной зависимости при помощи линий на плоскости. Графики используются для наглядного изображения функциональных зависимостей. В экономическом анализе применяются почти все виды графиков – диаграммы сравнения, диаграммы временных рядов, графики зависимости.

Широко применяется графический метод для исследования производственных процессов, организационных структур и т.д.

Особое место в экономическом анализе занимает построение сетевых графиков. Сетевой график позволяет выделить из всего комплекса работ наиболее важные, лежащие на критическом пути, и сосредоточиться именно на них. Наиболее часто сетевые графики применяются в строительстве. На стадии оперативного анализа и управления сетевой график дает возможность осуществлять действенный контроль за ходом строительства, своевременно принимать меры по устранению возможных задержек.

Кроме того, сетевые графики могут разрабатываться при описании технологии какого-либо производственного процесса. В данном случае задача составления сетевого графика несколько иная – скоординировать работу всех служб предприятия. Основные элементы сетевого графика – событие, работа, ожидание, зависимость. Каждый круг считается одной из вершин графика. Линия, соединяющая две вершины, означает проделанную работу. Над линией записывают наименование работы, а под линией – продолжительность данного этапа работ. Если из одной вершины ведет несколько путей, то это значит, что после выполнения данного этапа может быть несколько вариантов развития событий. Если это технологический сетевой график, то это будет означать, что возможно проведение одновременно нескольких работ (параллельная организация технологического процесса). Вершины могут просто нумероваться, а могут содержать информацию о накопленной продолжительности работы или стоимости данного этапа.

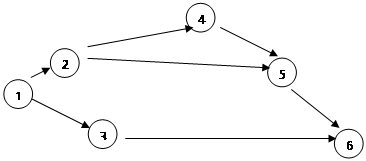
Рис. 3.1. Пример сетевого графика

Этапами разработки сетевого графика являются:

- сбор технической и технологической информации;

- составление таблицы работ и ресурсов в технологической последовательности, в которой указывается характеристика и объем работ, время, потребные ресурсы, порядок проведения (очередность);

- составление сетевого графика;

- определение критерия оптимизации (по экономии материальных, трудовых ресурсов, срокам, минимальной стоимости и т.п.);

- определение оптимального пути решения[1, c.85].

Похожие работы

Научные основы экономического анализа. Понятие и значение экономического анализа, его место в системе экономических наук

Скачать

64660

13

2

... в самостоятельную отрасль экономических знаний, он используется в экономической теории, народно-хозяйственном прогнозировании и статистике. Экономический анализ деятельности организаций обособился и занимает самостоятельное место в системе экономических наук и учебных дисциплин. Главное его обеспечение составляют системный бухгалтерский учет и бухгалтерская (финансовая) отчетность. Несмотря на ...

Теоретические основы экономического анализа

Скачать

57658

0

0

... перспективу. Вторая задача - оценка использования организациями своих материальных, трудовых и финансовых ресурсов. Наиболее рациональное и эффективное использование ресурсов - важнейшая экономическая задача. На основе экономического анализа дается оценка эффективности использования материальных, трудовых и финансовых ресурсов. В промышленности, например, в этом плане исследуются эффективность ...

Экономический анализ деятельности предприятия

Скачать

16878

8

0

... наличии каких бы то ни было инвестиций. В связи с этим расчет не может быть выполнен. Список используемой литературы 1.  Барнгольц С.Б., Мельник М.В. Методология экономического анализа деятельности хозяйствующего субъекта: Уч. пособие. – М.: Финансы и статистика, 2003. – 240 с.: ил. 2.  Барнгольц С.Б. Экономический анализ хозяйственной деятельности на современном этапе развития. // Финансы ...

Комплексный экономический анализ финансовой деятельности предприятия

Скачать

33676

15

2

... 232 21,907 Доля влияния фактора, % - - 100 0,327 101,208 0,927 -6,207 -7,916 103,532 10,871 1,535 0,365 5,432 -7,331   Вывод: Прибыль является результативным показателем деятельности предприятия. Снижение прибыли в отчетном периоде составило 298,842. При этом максимальное влияние оказало снижение цены единицы продукции типа А, что составило -16,232 %, прироста прибыли и 5,432% в ...