Навигация
Методы линейного и динамического программирования
3.2. Методы линейного и динамического программирования
Линейное программирование объединяет методы решения задач, которые описываются линейными уравнениями. Данный метод основан на решении системы линейных уравнений, когда зависимость между изучаемыми явлениями строго функциональна. С помощью этого метода в промышленном производстве, например, исчисляется оптимальная общая производительность машин, агрегатов, поточных линий. Все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. Решить такую задачу – значит выбрать из всех допустимых вариантов лучший, оптимальный.
Для решения задач линейного программирования могут быть использованы средства, включенные в состав электронных таблиц для персональных компьютеров. Из числа таких средств наиболее распространены таблицы программ MS Excel.
Постановка задачи линейного программирования состоит в формулировке целевой функции и ограничений – уравнений или неравенств.
Пример. Фирма производит продукцию двух видов – Х и У. Имеются следующие данные о производстве продукции:
| Цех | Продукция | Максимально возможная загрузка в неделю, час | |
| Х | У | ||
| Сборочный | 2 шт/час | 4 шт/час | 100 |
| Отделочный | 3 шт/час | 2 шт/час | 90 |
| Прибыль | 25 тыс.р./шт | 40 тыс.р./шт | Максимум |
Целевой функцией в данном случае является прибыль, которую необходимо максимизировать:
ВП = 25 * Х + 40 * У.
Имеются ограничения по производительности сборочного и отделочного цехов:
2 * Х + 4 * У меньше или равно 100;
3 * Х + 2 * У меньше или равно 90,
а также требование неотрицательности элементов – Х, У больше 0.
Решается методом итераций (подбора значений). После каждого шага проверяется соблюдение ограничений. В результате получаем решение Х=20, У = 15. Максимальная прибыль составит 1100 тыс.р. при полной загрузке обоих цехов.
В задачах линейного программирования может представлять интерес вопрос, имеет ли смысл увеличивать объем доступного ресурса. Например, какова цена увеличения рабочего времени в сборочном цехе на один час в неделю. Эта цена – добавочная валовая прибыль, которая может быть получена, называется двойственной оценкой данного ресурса. Двойственную оценку можно рассматривать как упущенную выгоду или как прибыль, недополученную в результате нехватки ресурса. Если в приведенном примере рабочую неделю в сборочном цехе увеличить на восемь часов, то новое оптимальное решение будет выглядеть следующим образом:
Х = 18;
У = 18.
Валовая прибыль при этом составит 1170 тыс.р.
Решение задач линейного программирования может проводиться графическим методом. Для этого найдем в плоскости координат область, соответствующую всем ограничениям.
Первые два ограничения можно представить в виде:
У ≤ 25 – 0,5 * Х;
У ≤ 45 – 1,5 * Х.
Двум оставшимся ограничениям соответствуют сами оси Х и У.
На рисунке линия номер один соответствует первому ограничению, линия номер два соответствует второму ограничению. Очевидно, что допустимая область решений находится в зоне, ограниченной пересечением двух прямых и осей координат.
Какая же точка этой области соответствует оптимальному решению? Целевая функция описывается выражением ВП = 25 * Х + 40 * У или У = ВП – 0,625 * Х .
Переменная ВП должна быть максимальна. График этой функции можно представить несколькими линиями при разных значениях ВП. На рисунке представлены три штриховые линии, соответствующие ВП = 5, 10, 15.
![]()
 45
45
2
 25
25
 15
15
 10
1
10
1
 5
5
![]() 8 16 24 30 50
8 16 24 30 50
Рис. 3.1. Решение задачи линейного программирования
Нетрудно заметить, что чем дальше от центра координат находится прямая, тем больше значение ВП. Это означает, что функция 25 * Х + 40 * У примет максимально значение в точке пересечении прямых 1 и 2. Координаты этой точки можно найти, решив систему линейных уравнений:
![]() У = 25 – 0,5 * Х У = 15;
У = 25 – 0,5 * Х У = 15;
У = 45 – 1,5 * Х Х = 20.
Методы динамического программирования применяются при решении задач оптимизации, которая описывается нелинейными функциями. Типичным примером является разновидность транспортной задачи, когда необходимо загрузить транспортное средство различными видами товаров, которые к тому же имеют различный вес, таким образом, чтобы стоимость груза являлась максимальной. Если обозначить:
В – максимальная загрузка транспортного средства;в – масса одного предмета каждого вида;
с – стоимость предмета каждого вида;
к – количество предметов каждого вида ,
тогда задача может быть описана уравнением
S к * с = макс при ограничении S к * в < В,
сумма от 1 до Н при этом Н – ассортимент загружаемой продукции. Задача решается в Н этапов, причем на первом этапе определяется максимальная стоимость груза из продукции первого типа, затем – первого и второго типов и так далее.
Похожие работы
... в самостоятельную отрасль экономических знаний, он используется в экономической теории, народно-хозяйственном прогнозировании и статистике. Экономический анализ деятельности организаций обособился и занимает самостоятельное место в системе экономических наук и учебных дисциплин. Главное его обеспечение составляют системный бухгалтерский учет и бухгалтерская (финансовая) отчетность. Несмотря на ...
... перспективу. Вторая задача - оценка использования организациями своих материальных, трудовых и финансовых ресурсов. Наиболее рациональное и эффективное использование ресурсов - важнейшая экономическая задача. На основе экономического анализа дается оценка эффективности использования материальных, трудовых и финансовых ресурсов. В промышленности, например, в этом плане исследуются эффективность ...
... наличии каких бы то ни было инвестиций. В связи с этим расчет не может быть выполнен. Список используемой литературы 1. Барнгольц С.Б., Мельник М.В. Методология экономического анализа деятельности хозяйствующего субъекта: Уч. пособие. – М.: Финансы и статистика, 2003. – 240 с.: ил. 2. Барнгольц С.Б. Экономический анализ хозяйственной деятельности на современном этапе развития. // Финансы ...
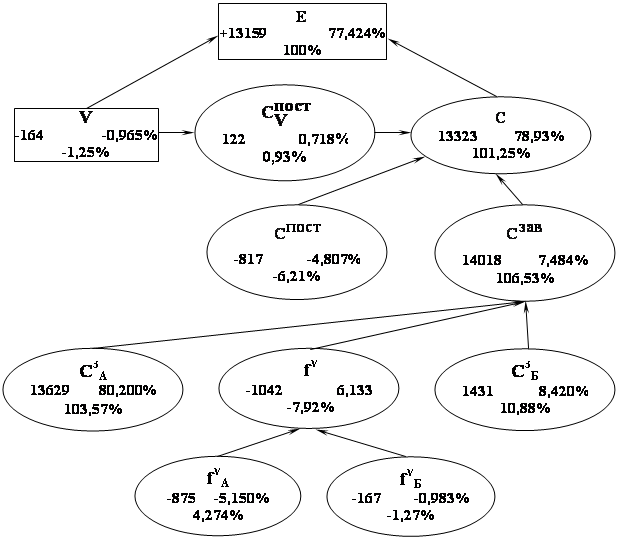
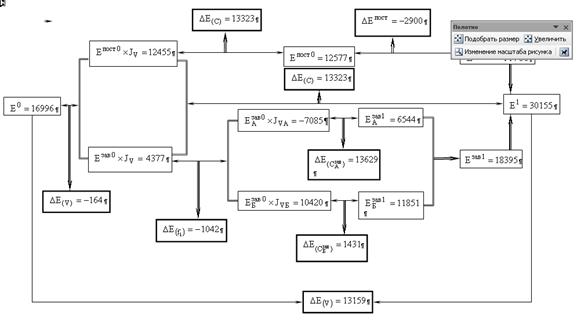
... 232 21,907 Доля влияния фактора, % - - 100 0,327 101,208 0,927 -6,207 -7,916 103,532 10,871 1,535 0,365 5,432 -7,331 Вывод: Прибыль является результативным показателем деятельности предприятия. Снижение прибыли в отчетном периоде составило 298,842. При этом максимальное влияние оказало снижение цены единицы продукции типа А, что составило -16,232 %, прироста прибыли и 5,432% в ...

0 комментариев