Уравнения движения электропривода

2. Уравнения движения электропривода

Механическая часть электропривода представляет собой систему твердых тел, на движение которых наложены ограничения, определяемые механическими связями Уравнения механических связей устанавливают соотношения между перемещениями в системе, а в тех случаях, когда задаются соотношения между скоростями ее элементов, соответствующие уравнения связей обычно интегрируются В механике такие связи называются голономными В системах с голономными связями число независимых переменных - обобщенных координат, определяющих положение системы, - равно числу степеней свободы системы Известно, что наиболее общей формой записи дифференциальных уравнений движения таких систем являются уравнения движения в обобщенных координатах (уравнения Лагранжа)

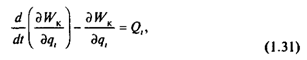
где W_K - запас кинетической энергии системы, выраженный через обобщенные координаты q_i и обобщенные скорости _i; Q_i=dA_i/dq_i - обобщенная сила, определяемая суммой элементарных работ dА₁ всех действующих сил на возможном перемещении dq_i, или

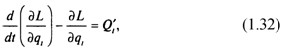
где L - функция Лагранжа, Q'_i - обобщенная сила, определяемая суммой элементарных работ dA, всех внешних сил на возможном перемещении dq_i. Функция Лагранжа представляет собой разность кинетической W_K и потенциальной W_п энергий системы, выраженных через обобщенные координаты q_i и обобщенные скорости _i, т е:

Уравнения Лагранжа дают единый и достаточно простой метод математического описания динамических процессов в механической части привода; их число определяется только числом степеней свободы системы.

В качестве обобщенных координат могут быть приняты как различные угловые, так и линейные перемещения в системе Поэтому при математическом описании динамики механической части привода с помощью уравнений Лагранжа предварительного приведения ее элементов к одной скорости не требуется. Однако, как было отмечено, до выполнения операции приведения в большинстве случаев невозможно количественно сопоставлять между собой различные массы системы и жесткости связей между ними, следовательно, невозможно выделить главные массы и главные упругие связи, определяющие минимальное число степеней свободы системы, подлежащее учету при проектировании. Поэтому составление приведенных расчетных механических схем и их возможное упрощение являются первым важным этапом расчета сложных электромеханических систем электропривода независимо от способа получения их математического описания.

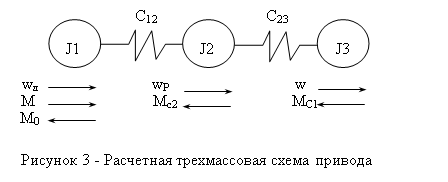
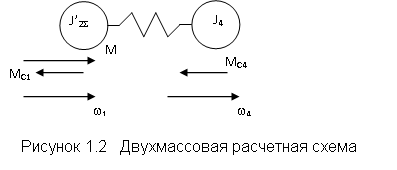
Получим уравнения движения, соответствующие обобщенным расчетным механическим схемам электропривода, представленным на рис.1.2. В трехмассовой упругой системе обобщенными координатами являются угловые перемещения масс f₁, f₂, f₃, им соответствуют обобщенные скорости w₁, w₂ и w₃. Функция Лагранжа имеет вид:

Для определения обобщенной силы Q'₁ необходимо вычислить элементарную работу всех приложенных к первой массе моментов на возможном перемещении

Следовательно,

Аналогично определяются две другие обобщенные силы:

Подставляя (1.34) в (1.32) и учитывая (1.35) и (1.36), получаем

следующую систему уравнений движения:

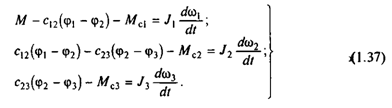В (1.37) пропорциональные деформациям упругих связей моменты

являются моментами упругого взаимодействия между движущимися массами системы:

С учетом (1.38) систему уравнений движения можно представить в виде

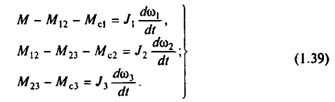
Рассматривая (1.39), можно установить, что уравнения движения приведенных масс электропривода однотипны. Они отражают физический закон (второй закон Ньютона), в соответствии с которым ускорение твердого тела пропорционально сумме всех приложенных к нему моментов (или сил), включая моменты и силы, обусловленные упругим взаимодействием с другими твердыми телами системы.

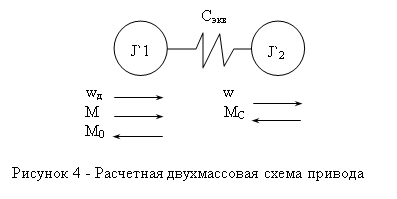
Очевидно, повторять вывод уравнений движения вновь, переходя к рассмотрению двухмассовой упругой системы, нет необходимости. Движение двухмассовой системы описывается системой (1.39) при J₃=0 и М₂₃=0

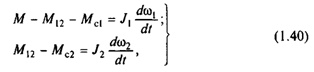
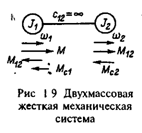
Переход от двухмассовой упругой системы к эквивалентному жесткому приведенному механическому звену для большей наглядности его физической сути полезно выполнить в два этапа. Вначале положим механическую связь между первой и второй массами (см. рис.1.2,б) абсолютно жесткой (с₁₂=¥). Получим двухмассовую жесткую систему, расчетная схема которой показана на рис.1.9. Отличием ее от схемы на рис.1.2,б является равенство скоростей масс w₁=w₂=w_i, при этом в соответствии со вторым уравнением системы (1.40)

Уравнение (1.41) характеризует нагрузку жесткой механической связи при работе электропривода. Подставив это выражение в первое уравнение системы (1.40), получим

Следовательно, с учетом обозначений на рис.1.2,в М_С=М_С1+М_с2; J_S=J₁+J₂ Уравнение движения электропривода имеет вид

Это уравнение иногда называют основным уравнением движения электропривода. Действительно, значение его для анализа физических процессов в электроприводе исключительно велико. Как будет показано далее, оно правильно описывает движение механической части электропривода в среднем. Поэтому с его помощью можно по известному электромагнитному моменту двигателя и значениям М_с и J_S оценить среднее значение ускорения электропривода, предсказать время, за которое двигатель достигнет заданной скорости, и решить многие другие практические вопросы даже в тех случаях, когда влияние упругих связей в системе существенно.

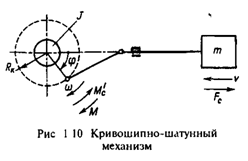
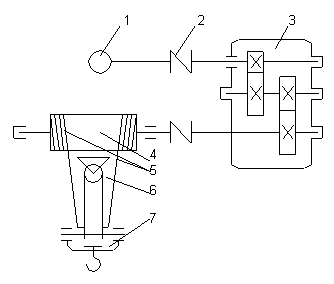
Как было отмечено, передачи ряда электроприводов содержат нелинейные кинематические связи, типа кривошипно-шатунных, кулисных и других подобных механизмов. Для таких механизмов радиус приведения является переменной величиной, зависящей от положения механизма, и при получении математического описания необходимо это обстоятельство учитывать. В частности, для приведенной на рис.1.10 схемы кривошипно-шатунного механизма

где R_k - радиус кривошипа.

Имея в виду механизмы, аналогичные показанному на рис.1.10, рассмотрим двухмассовую систему, первая масса которой вращается со скоростью двигателя w и представляет собой суммарный приведенный к валу двигателя момент инерции всех жестко и линейно связанных вращающихся элементов J₁ а вторая масса движется с линейной скоростью v и представляет собой суммарную массу т элементов, жестко и линейно связанных с рабочим органом механизма. Связь между скоростями w и v нелинейная, причем r = r(f). Для получения уравнения движения такой системы без учета упругих связей воспользуемся уравнением Лагранжа (1.31), приняв в качестве обобщенной координаты угол ф. Вначале определим обобщенную силу:

где М_с' - суммарный момент сопротивления от сил, воздействующих на линейно связанные с двигателем массы, приведенный к валу двигателя; F_c - результирующая всех сил, приложенных к рабочему органу механизма и линейно связанным с ним элементам; dS - возможное бесконечно малое перемещение массы т. Следовательно,

где r(f)=dS/df - радиус приведения

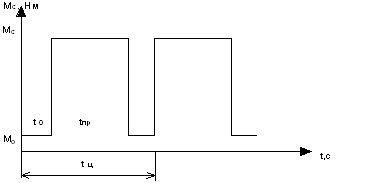
При наличии нелинейной механической связи рассматриваемого типа момент статической нагрузки механизма содержит пульсирующую составляющую нагрузки, изменяющуюся в функции угла поворота f:

Запас кинетической энергии системы

здесь J_S(f)=J₁+mr²(f) - суммарный приведенный к валу двигателя момент инерции системы.

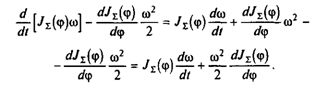
В применении к данному случаю левая часть уравнения (1.31) записывается так:

Таким образом, в рассматриваемом случае уравнение движения жесткого приведенного звена имеет вид

Рассматривая (1.45), нетрудно установить, что при наличии нелинейных механических связей уравнение движения электропривода существенно усложняется, так как становится нелинейным, содержит переменные коэффициенты, зависящие от углового перемещения ротора двигателя, и момент нагрузки, являющийся периодической функцией угла поворота. Сравнив это уравнение с основным уравнением движения (1.42), можно убедиться, что использовать основные уравнение движения электропривода допустимо лишь при постоянстве момента инерции J_S=const.

В случаях, когда момент инерции при работе электропривода изменяется из-за внешних воздействий, вне связи с собственным движением, уравнение движения электропривода принимает несколько иной вид Такие условия возникают при работе машин, в которых перемещение рабочего органа по пространственным траекториям осуществляется несколькими индивидуальными электроприводами, предусмотренными для каждой координаты перемещения (экскаваторы, краны, роботы и т.п.). Например, момент инерции электропривода поворота робота зависит от вылета схвата относительно оси вращения. Изменения вылета схвата не зависят от работы электропривода поворота, они определяются движением электропривода изменения вылета. В подобных случаях приведенный момент инерции электропривода поворота следует полагать независимой функцией времени J_S(t). Соответственно, левая часть уравнения (1.31) запишется так:

а уравнение движения электропривода примет вид:

Функции J_S(t) и M_c(t) при этом следует определить путем анализа движения электропривода, вызывающего изменения момента инерции и нагрузки, в рассматриваемом примере это электропривод механизма изменения вылета схвата.

Полученные математические описания динамических процессов в механической части электропривода, представляемой обобщенными схемами, позволяют анализировать возможные режимы движения электропривода. Условием динамического процесса в системе, описываемой (1.42), является dw/dt¹0, т.е. наличие изменений скорости электропривода. Для анализа статических режимов работы электропривода необходимо положить dw/dt=0. Соответственно уравнение статического режима работы электропривода с жесткими и линейными механическими связями имеет вид

Если при движении М¹М_с, dw/dt¹0, то имеет место или динамический переходный процесс, или установившийся динамический процесс. Последнее соответствует случаю, когда приложенные к системе моменты содержат периодическую составляющую, которая после переходного процесса определяет принужденное движение системы с периодически изменяющейся скоростью.

В механических системах с нелинейными кинематическими связями (рис.1.10) в соответствии с (1.45) статические режимы работы отсутствуют. Если dw/dt=0 и w=const, в таких системах имеет место установившийся динамический процесс движения. Он обусловлен тем, что массы, движущиеся линейно, совершают принужденное возвратно-поступательное движение, и их скорость и ускорение являются переменными величинами.

С энергетической точки зрения режимы работы электропривода разделяются на двигательные и тормозные, отличающиеся направлением потока энергии через механические передачи привода (см. §1.2). Двигательный режим соответствует прямому направлению передачи механической энергии, вырабатываемой двигателем, к рабочему органу механизма. Этот режим обычно является основным для проектирования механического оборудования, в частности редукторов. Однако при работе электропривода достаточно часто складываются условия для обратной передачи механической энергии от рабочего органа механизма к двигателю, который при этом должен работать в тормозном режиме. В частности, для электроприводов с активной нагрузкой двигательный и тормозной режимы работы вероятны практически в равной степени. Тормозные режимы работы электропривода возникают также в переходных процессах замедления системы, в которых освобождающаяся кинетическая энергия может поступать от соответствующих масс к двигателю.

Изложенные положения позволяют сформулировать правило знаков момента двигателя, которое следует иметь в виду при использовании полученных уравнений движения. При прямом направлении передачи механической мощности Р=Мw ее знак положителен, следовательно, движущие моменты двигателя должны иметь знак, совпадающий со знаком скорости. В тормозном режиме Р<О, поэтому тормозные моменты двигателя должны иметь знак, противоположный знаку скорости.

При записи уравнений движения были учтены направления моментов, показанные на обобщенных расчетных схемах, в частности на рис.1.2,в. Поэтому правило знаков для моментов статической нагрузки другое: тормозные моменты нагрузки должны иметь знак, совпадающий со знаком скорости, а движущие активные нагрузки - знак, противоположный знаку скорости.