Навигация
Механическая часть электропривода как объект управления
3. Механическая часть электропривода как объект управления
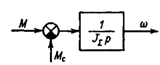
Полученные уравнения движения позволяют проанализировать динамические особенности механической части электропривода как объекта управления, пользуясь методами теории автоматического управления. Основой для анализа являются структурные схемы, вид которых определяется принятой расчетной схемой механической части.
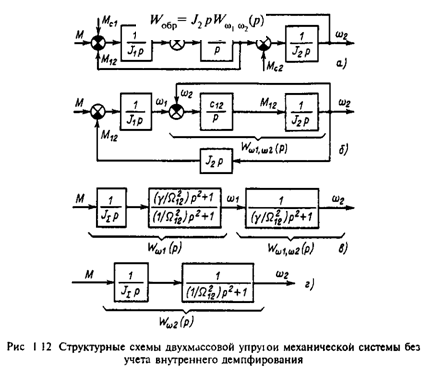
Получим структурные схемы для расчетных схем, представленных на рис.1.2, с их помощью проведем анализ свойств механической части электропривода и оценим погрешности, вносимые пренебрежением упругими механическими связями.
Для получения структурной схемы трехмассовой упругой механической системы продифференцируем (1.38):
![]()
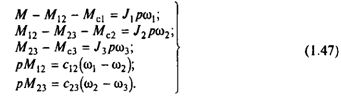 |
Далее положим в (1.39) и (1.46) d/dt =p, получим
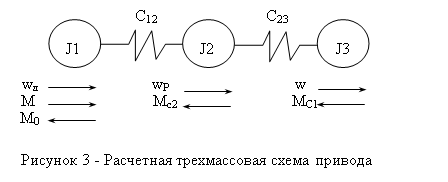
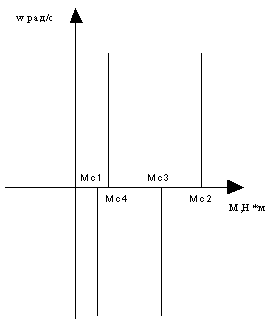
Системе уравнений (1.47) соответствует структурная схема, приведенная на рис.1.11,а. Она дает представление о механической части электропривода в виде трехмассовой упругой системы как об объекте управления. Управляющим воздействием здесь является электромагнитный момент двигателя М, а возмущениями - моменты нагрузки Мс1, Мс2 и Мс3. Регулируемыми переменными могут быть скорости w1, w2 и w3, перемещения f1, f2 и f3, а также нагрузки упругих связей М12 и М23. Структурно механическая часть электропривода представляет собой сложный объект, состоящий из цепочки интегрирующих звеньев, замкнутых перекрестными внутренними обратными связями.
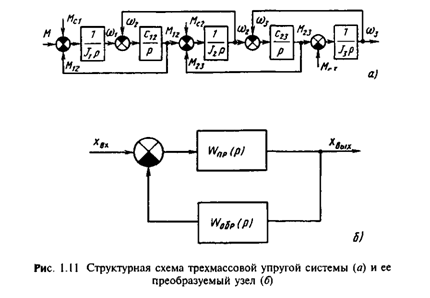
Напомним читателю известный из теории автоматического регулирования простейший способ преобразования структурных схем и получения передаточных функций для замкнутых обратными связями систем, который при необходимости используется в дальнейшем изложении. На рис.1.11,б представлен узел структурной схемы, в котором выделена передаточная функция Wпр(р), соответствующая прямой передаче сигнала, и передаточная функция Woбp(p) обратной связи. Передаточная функция замкнутого контура
Путем преобразований структуры (рис.1.11,о) с помощью формулы (1.48), получим передаточную функцию механической части по управляющему воздействию при выходной переменной w1(р):
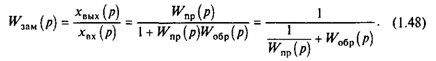
Характеристическое уравнение запишем в виде
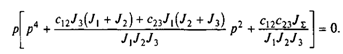
Решив биквадратное уравнение, получим корни характеристического уравнения системы:
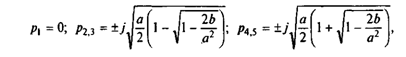
где
![]()
Анализ корней показывает, что при всех реальных сочетаниях параметров подкоренные выражения представляют собой действительные положительные числа. Следовательно, р1=0; р23=±jW1;p45=±jW2.
Корни характеристического уравнения свидетельствуют о том, что система может быть представлена в виде последовательного соединения интегрирующего звена и двух консервативных колебательных звеньев с резонансными частотами колебаний W1 и W2. При изменении момента М(р) скачком в системе могут возникать незатухающие колебания с частотами W1 и W2, а когда частота возмущающих воздействий совпадает с одной из этих частот, в системе развивается недемпфированный резонанс, при котором амплитуды колебаний теоретически могут возрастать до бесконечности. Реально в системе присутствуют диссипативные силы, которые демпфируют колебания, ограничивая резонансные амплитуды большими, но конечными значениями.
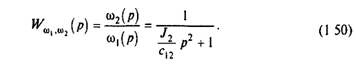 |
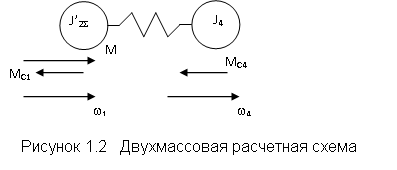
Более детальный анализ свойств упругих механических систем можно провести на основе двухмассовой расчетной схемы, структура которой представлена на рис.1.12,а. Она составлена на основе (1.47) при М23=0, Mc3=0 и J3=0. Для исследования свойств этой системы как объекта управления примем возмущения Мс1=Мс2=0 и выполним показанные на рис.1.12,б-г преобразования ее структуры. Прежде всего перенесем внутреннюю связь по упругому моменту на выход системы, как показано на рис.1.12,б. Эта операция позволит с помощью (1.48) определить передаточную функцию, связывающую выходную координату со скоростью w1:
Далее находим передаточную функцию двухмассовой системы по управлению при выходной переменной w1 аналогично рассмотренной выше для трехмассовой системы (1.49). В соответствии со схемой рис.1.12,б передаточная функция прямого канала
![]()
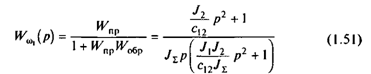 |
Следовательно, искомая передаточная функция с учетом (1.50) определяется так:
Характеристическое уравнение системы
Корни характеристического уравнения
где W12 - резонансная частота двухмассовой упругой системы.
![]()
Сравнение (1.52) с корнями (1.49) показывает, что при переходе от трехмассовой упругой системы к двухмассовой выявляется только одна частота W12, на которой возможно проявление механического резонанса. Однако, если при этом значение W12 оказывается достаточно близким к одной из парциальных частот исходной системы W1 или W2, можно полагать, что двухмассовая система правильно отражает главные особенности механической части электропривода.
Для удобства анализа введем следующие обобщенные параметры двухмассовой упругой системы: g=(J1+ J2)/J1=JS/J1 - соотношение масс;
![]() - резонансная частота системы;
- резонансная частота системы;
![]() -резонансная частота второй массы при жесткой заделке первой (J1®¥)
-резонансная частота второй массы при жесткой заделке первой (J1®¥)
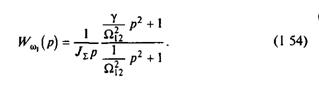
С учетом этих обозначений (1.50) и (1.51) могут быть представлены в виде:
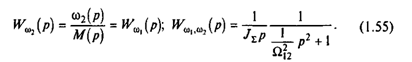 |
Полученные соотношения (1.53) и (1.54) позволяют представить механическую часть электропривода как объект управления в виде трех звеньев, показанных на рис.1.12,в. С помощью этой схемы нетрудно записать и передаточную функцию системы по управляющему воздействию при выходной переменной w2:
Передаточной функции (1.55) соответствует структурная схема объекта, представленная на рис.1.12,г. Для анализа свойств системы воспользуемся частотным методом теории управления. Уравнение амплитудно-фазовой характеристики (АФХ) получим, подставив в (1.54) р=jW:
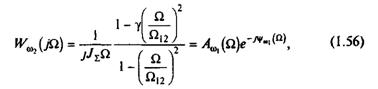
где Aw1(W) - амплитудно-частотная характеристика (АЧХ); Yw1(W) - фазо-частотная характеристика (ФЧХ) объекта при выходной переменной w1.
Прежде чем перейти к построению логарифмических частотных характеристик, необходимо обратить внимание на то, что при анализе механической и электрической частей системы электропривода здесь и в дальнейшем рассматриваются их передаточные функции, в которых выходная и входная переменные чаще всего имеют различные единицы измерения В этих случаях W(jW) представляет собой не комплексный коэффициент усиления, а комплексный коэффициент передачи, имеющий определенную единицу измерения В частности, в (1.56) его единица 1/(Н м·с), такую же размерность имеет величина Аw1(W).
При необходимости все дифференциальные уравнения и передаточные функции системы могут быть представлены в относительных единицах. Эта возможность используется при расчетах и исследованиях электроприводов.
В данном курсе, чтобы не осложнять понимание физического смысла явлений и параметров, представление переменных в относительных единицах, как правило, не используется. При этом для выражения АЧХ в логарифмическом масштабе единицы амплитуд опускаются, что соответствует относительным их значениям при базовом значении, равном единице измерения.
 |
Асимптотические логарифмические АЧХ (ЛАЧХ) могут быть построены непосредственно по полученным передаточным функциям системы. В частности, в соответствии с (1.54) система может быть представлена последовательным соединением интегрирующего звена, форсирующего звена второго порядка с частотой сопряжения Wc1=W12/
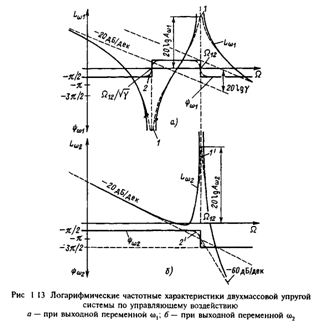
Соответствующая всем изложенным положениям ЛАЧХ объекта при выходной переменной w1 представлена на рис.1.13,а. Там же построена его ЛФЧХ на основе уравнения АФХ (1.56). В низкочастотной области сдвиг между колебаниями определяется интегрирующим звеном и составляет -90°. При W=W12/![]() скачком меняет знак числитель (1.56), что соответствует уменьшению фазового сдвига на 180°. Затем на частоте W=W12 аналогично изменяется знак знаменателя, и фазовый сдвиг вновь принимает значение -90° в соответствии с высокочастотной асимптотой ЛАЧХ На рис.1.13,б представлены логарифмические частотные характеристики механической части электропривода по управлению при выходной переменной w2. Они построены по передаточной функции (1.55), которой соответствует АФХ, отличающаяся от (1.56) только равенством числителя единице при всех частотах. В низкочастотной области ЛАЧХ Lw2 совпадает с Lw1, разрыв имеет место только на резонансной частоте W12 и в высокочастотной области стремится к асимптоте с наклоном -60 дБ/дек. Соответственно фазовый сдвиг между колебаниями при этом составляет -270°.
скачком меняет знак числитель (1.56), что соответствует уменьшению фазового сдвига на 180°. Затем на частоте W=W12 аналогично изменяется знак знаменателя, и фазовый сдвиг вновь принимает значение -90° в соответствии с высокочастотной асимптотой ЛАЧХ На рис.1.13,б представлены логарифмические частотные характеристики механической части электропривода по управлению при выходной переменной w2. Они построены по передаточной функции (1.55), которой соответствует АФХ, отличающаяся от (1.56) только равенством числителя единице при всех частотах. В низкочастотной области ЛАЧХ Lw2 совпадает с Lw1, разрыв имеет место только на резонансной частоте W12 и в высокочастотной области стремится к асимптоте с наклоном -60 дБ/дек. Соответственно фазовый сдвиг между колебаниями при этом составляет -270°.
Проанализируем основные свойства механической части, воспользовавшись ее структурой, представленной на рис.1.12,в, и частотными характеристиками, изображенными на рис.1.13 При этом обратим внимание на различия во влиянии упругости на движение первой и второй масс. Движение первой массы при небольших частотах колебаний управляющего воздействия М в соответствии с (1.54) и рис.1.13,а определяется суммарным моментом инерции электропривода JS, причем механическая часть ведет себя как интегрирующее звено. В частности, при М=const скорость w1 изменяется по линейному закону, на который накладываются колебания, обусловленные упругой связью. Иными словами, интегрирующее звено в структуре на рис.1.12,б характеризует условия движения механической части в среднем.
При приближении частоты колебаний момента к резонансной W12 амплитуды колебаний скорости w1 возрастают и при W1=W12 стремятся к бесконечности. Однако проявления резонанса существенно зависят от параметров механической части в связи с наличием в числителе передаточной функции Ww1 форсирующего звена второго порядка. Можно выявить условия, при выполнении которых влияние упругости на движение
 |
первой массы будет незначительным.
Рис 1.14 Структурная схема механической части с жесткими механическими связями.
Во-первых, из (1.54) непосредственно следует, что если механизм обладает небольшой инерцией (J2<<J1, g®1), то движение первой массы близко к движению, определяемому интегрирующим звеном Wи=JS/p. Во-вторых, из (1.56) видно, что при W12®¥ в области малых и средних частот движение первой массы определяется тем же интегрирующим звеном. Отсюда вытекает важный практический вывод. Если при синтезе электропривода используются обратные связи только по переменным двигателя, то при J2<<J1 или W12>>Wc где Wс - частота среза желаемой ЛАЧХ разомкнутого контура регулирования, механическую часть электропривода можно представить жестким механическим звеном, не учитывая влияния упругостей.
В соответствии с (1.55) и рис.1.13,б колебательность второй массы выше, чем первой. В низкочастотной области асимптоты ЛАЧХ Lw1 и Lw2 совпадают, так как в среднем движение второй массы также определяется интегрирующим звеном Wи=JS/p. Однако при W>W2 наклон высокочастотной асимптоты Lw2 составляет -60 дБ/дек, и нет факторов, которые ослабляли бы развитие резонансных колебаний при любых g.
Следовательно, во всех случаях, когда важно получить требуемое качество движения второй массы, а также при регулировании ее координат, пренебрегать влиянием упругости механических связей без необходимой проверки нельзя. Достаточным условием для неучета упругости является только большая частота резонанса W12, существенно выходящая за пределы полосы пропускания частот электропривода. В реальных системах присутствуют диссипативные силы, которые оказывают на колебательную систему демпфирующее действие. Это демпфирование в большинстве случаев невелико. По данным технической литературы естественное затухание колебаний под действием внутренних сил вязкого трения можно характеризовать значениями логарифмического декремента
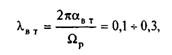
где aвт и Wp=W12 - коэффициент затухания и резонансная частота колебаний с учетом влияния внутренних диссипативных сил.
Учет естественного демпфирования существенно не сказывается на форме ЛАЧХ и ЛФЧХ системы, однако, ограничивает резонансный пик конечными значениями, как показано штриховой кривой 1 на рис.1.13,а, и несколько сглаживает фазочастотную характеристику (штриховая кривая 2 на том же рисунке). Аналогичные изменения, вносимые естественным демпфированием в частотные характеристики на рис.1 13,б, показаны штриховыми кривыми, обозначенными соответственно 1' и 2'.
Сочетания параметров, при которых J2<<J1 или W2®¥, Достаточно распространены, поэтому в дальнейшем изложении во всех случаях, когда это допустимо, используется представление механической части электропривода в виде жесткого приведенного звена. Уравнению движения (1.42) для этого случая при р=d/dt соответствует структурная схема, представленная на рис.1.14. Она совпадает с входным звеном в рассмотренной выше структуре рис.1.12,в, и частотные характеристики жесткой механической части электропривода в низкочастотной области не отличаются от приведенных на рис.1.13.
Похожие работы
... В результате получаем, что максимальную взвешенную сумму имеет следующий привод: преобразователь частоты – асинхронный двигатель. Следовательно, данный привод и подлежит дальнейшему расчету. 4. Расчет силового электропривода 4.1 Расчет параметров и выбор двигателя Расчетный режим работы двигателя – длительный с переменной нагрузкой, так как в процессе работы двигателя паузы отсутствуют ...
... о выборе лучшего варианта привода принимается на основе сопоставления приведенных затрат на одинаковый объем выпускаемой продукции. В данном проекте необходимо обеспечить регулирование продолжительности времени выпечки с коррекцией по температуре во второй зоне пекарной камеры. При этом необходимо учитывать, что производительность печи при замене системы привода меняться не должна, а также ...
... , кроме того, необходимо учитывать, что приводной двигатель будет обладать достаточно большой мощностью. При анализе литературных источников удалось установить, что в главных электроприводах прокатных станов холодной прокатки применяются две системы: а) УВ – ДПТ; б) Г – Д; Можно также рассмотреть варианты применения следующих систем: в) АД с частотным управлением; г) Каскадная система; д) ...
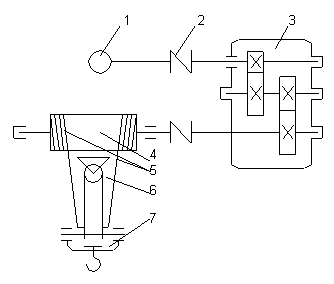
... рабочей машины. Характеристики представлены на рисунке 1.4. Рисунок 1.4 – Механические характеристики рабочей машины 2. Анализ и описание системы “Электропривод - сеть” и “Электропривод - оператор” Электропривод механизма подъема мостового крана питается стандартным трехфазным напряжением 380 В частотой 50 Гц. В промышленной сети возможны значительные броски напряжения, а также ...




0 комментариев