Навигация
Принят синусоидальный закон колебаний (рис. 1.3, а)
1. Принят синусоидальный закон колебаний (рис. 1.3, а).
2. Время одного цикла называют периодом Т. Если задан ресурс L, то общее число циклов N = L / T.
3. Наибольшее smax и наименьшее smin напряжения – величины алгебраические (со знаками).
4. Коэффициент асимметрии цикла R = smin / smax.
5. Среднее напряжение sm = (smax + smin) / 2 = 0,5 (1 + R) smax – постоянная составляющая цикла.
6. Амплитуда sа = (smax – smin) / 2 = 0,5 (1 – R) smax – переменная часть цикла, наиболее опасная для прочности, показывающая размах колебаний относительно среднего постоянного уровня.
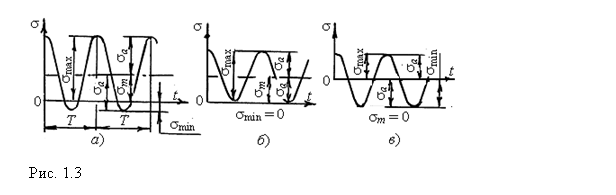
Если |smax| ¹ |smin|, то цикл называют асимметричным.
Если smin = 0, то R = 0, sm = sа = 0,5smax – цикл отнулевой (рис. 1.3, б).
Если |smax| = |smin| и smax> 0, а smin < 0 (рис. 1.3, в), то R = –1, sm = 0, sа = smax – цикл симметричный, самый опасный для прочности (sа = smax).
Если R = +1, то smax = smin. По величине и по знаку – это постоянные напряжения.
Примечание. Все, что касается в этом разделе нормальных напряжений s, относится
и к касательным напряжениям t с заменой в формулах символа s на t.
Во всех реальных деталях имеются микротрещины, включения, несплошности, нарушения структуры, т.е. дефекты. При переменных напряжениях микротрещины (и другие дефекты), развиваясь (с наработкой числа циклов), приводят к усталостной трещине, которая проникает в глубь сечения и вызывает усталостное разрушение детали. Процесс накопления повреждений называют усталостью. Усталостное разрушение происходит при меньших напряжениях, чем sВ или sТ.
1.3.2 Пределы выносливости
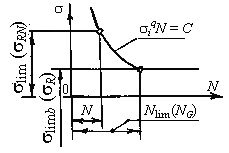
Циклическая долговечность материалов при переменных напряжениях характеризуется кривыми усталости (кривыми Велера). Кривые усталости (рис. 1.4) получают экспериментально на стандартных образцах, задавая им различные величины напряжений smax и фиксируя число циклов N, при которых происходит разрушение образцов.
Уравнение кривой усталости: siqNi = C,
где С – постоянная, соответствующая условиям проведения эксперимента.
Пределом выносливости материала называют максимальное напряжение, которое может выдержать образец материала при наработке заданного числа циклов.
Как показывает опыт, кривые усталости имеют два характерных участка: левый наклонный и правый горизонтальный (рис. 1.4). Абсциссу точки перелома Nlim (NG) кривой усталости называют базовым числом циклов, а соответствующий ему предел выносливости – пределом длительной выносливости (или базовым) slimb (sR). Например, для образцов черных металлов Nlim = 107, для цветных сплавов Nlim = (5…10) 107.
|
Рис. 1.4
При N < Nlim имеет место предел ограниченной выносливости slim (sRN).
Как видно из рис. 1.4, чем выше напряжение s, тем раньше начнется усталостное разрушение.
Связь между пределами выносливости по уравнению Велера:
slimqN = slimbq Nlim, откуда slim = slimbKL,
где KL = (Nlim / N)1/ q называют коэффициентом долговечности.
При N ³ Nlim принимают KL = 1.
Показатель степени q зависит от материала, термообработки, вида напряжений, влияния условий эксперимента и т.д. Он колеблется от 4 до 20, и его значения рекомендуются в каждом конкретном случае расчета детали (узла).
Пределы выносливости материалов (кривые усталости) определяют на стандартных испытательных образцах. Образец – это гладкий цилиндрический стержень малого диаметра (например, 10 мм) со свободной полированной поверхностью без упрочнения и термообработки. Нет нужды доказывать, что реальные детали отличаются от образцов формой, наличием на поверхностях посадок и других концентраторов напряжений (резьба, пазы, шлицы, галтели и др.), размерами, термообработкой, шероховатостью. Все эти отличия влияют на прочность и обязательно должны учитываться при расчетах.
В общем случае предел выносливости детали при асимметричном цикле нагружения:
slimD = 2s-1 / [(1 – R) KsD / KLs + ysD(1 + R)], (1.2)
(tlimD – то же с заменой символов s на t),
где s-1 – предел длительной выносливости образца при симметричном цикле нагружения, МПа; R – коэффициент асимметрии цикла; KsD = (Ks /Kds +1/KFs – – 1) / KV – коэффициент снижения предела выносливости при переходе от образца к реальной детали. Здесь Ks – эффективный коэффициент концентрации напряжений; Kds – коэффициент влияния размеров детали; KFs – коэффициент влияния качества (шероховатости) поверхности; KV – коэффициент влияния поверхностного упрочнения (термообработки); ysD – коэффициент влияния асимметрии цикла напряжений; KLs = (NlimD / NE)1/ q – коэффициент долговечности детали (узла). Здесь NlimD – базовое число циклов детали; NЕ– эквивалентное число циклов изменения напряжений:
NE = S [(si / smax)qNi], (1.3)
где smax – напряжение от длительно действующей максимальной нагрузки переменного режима; si и Ni – постоянное напряжение и соответствующее ему число циклов i-го постоянного блока циклограммы нагружения.
Коэффициенты в формуле (1.2) выбираются по справочникам.
Похожие работы
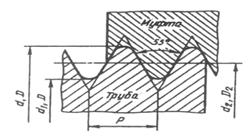
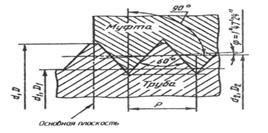
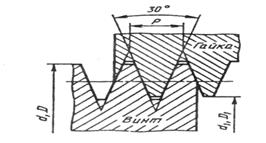
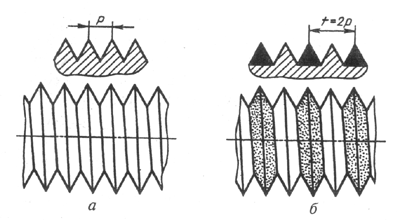
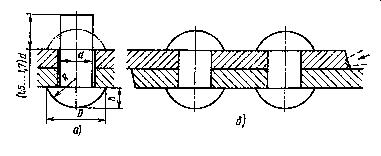
... приведенных на рисунке 4. В обозначение резьбы входят слово Резьба и все необходимые размеры, и предельные отклонения, а также сведения о числе заходов, направлении резьбы. Условное изображение резьбы в сборе На разрезах резьбового соединения в изображении на плоскости, параллельной его оси в отверстии, показывают только ту часть резьбы, которая не закрыта резьбой стержня. Штриховку в ...
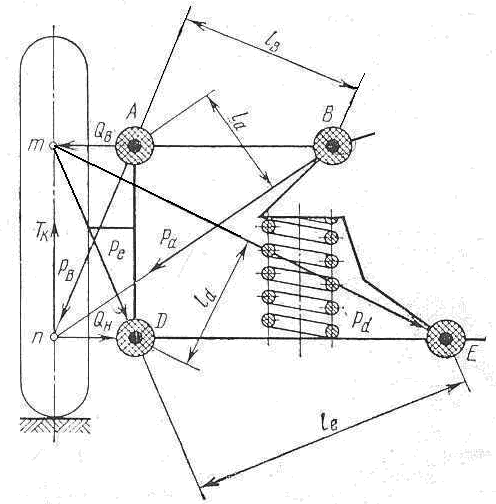
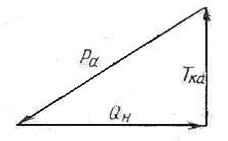
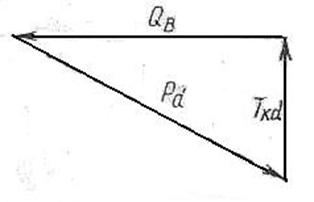
... . Наряду с названными выше шарнирными соединениями в современных подвесках применяются соединения обычных типов. Однако применение таких соединений непрерывно сокращается. В данном курсовом проекте мы заменим резьбовые соединения рычагов подвески автомобиля ГАЗ-24 на резинометаллические шарниры и рассмотрим их влияние на жесткость подвески. 1. Исходные данные В = 2,8 м. - база подвески; ...
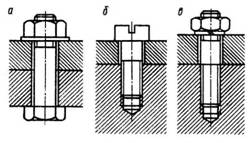
... выполнить сквозное отверстие и материал этой детали (с резьбой) не обладает высокими прочностными свойствами (пластмасса, алюминиевые, магниевые сплавы). Поэтому применение винта при частой разборке и сборке соединения из-за малой прочности резьбы не рекомендуется. Шпилька же ввинчивается в деталь с резьбой малой прочности только один раз – при сборке, при последующих разборках и сборках будет ...
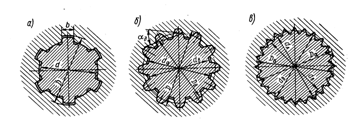
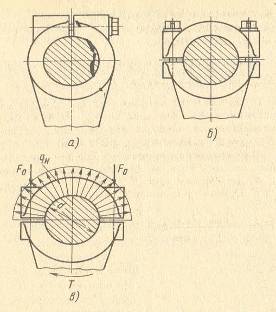
... болта. Обычно назначают σ0 = (0,4?0,7) σT. Для того чтобы соединения работали в расчетных силовых условиях, необходимо контролировать затяжку соединений. 14. Соединения с натягом Соединение деталей машин с натягом - разностью посадочных размеров - осуществляют за счет их предварительной деформации. С помощью натяга соединяют обычно детали с цилиндрическими и реже коническими ...

0 комментариев