Навигация
Метод Неймана-Коппа
2.1.1 Метод Неймана-Коппа
В этом случае используется правило сложения теплоемкостей элементов, составляющих соединение, а именно:
Cp = ![]() , (1)
, (1)
где cp– теплоемкость соединения, ср,i – теплоемкость составляющего его i – го элемента (с учетом количества атомов).
Установлено, что погрешность расчета по данному методу не превышает допустимую при расчете термодинамических величин (8%) [18].
2.1.2 Методы приближенного расчета энтропии и теплот образования веществ
В соответствии с индивидуальной температурной зависимостью теплот образования веществ и их энтропий:
![]() =
=![]() +
+ 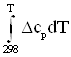 ; (2)
; (2)
S0T,i = ΔS0298, i+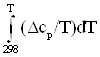 ; (3)
; (3)
При наличии рассчитанных интегралов задача сводится к определению ![]() и ΔS0298, i, для большинства соединений являющихся справочными величинами; в случае необходимости вычисления приведенных характеристик для малоизученных соединений применяют приближенные методы расчета, некоторые из которых рассмотрены ниже.
и ΔS0298, i, для большинства соединений являющихся справочными величинами; в случае необходимости вычисления приведенных характеристик для малоизученных соединений применяют приближенные методы расчета, некоторые из которых рассмотрены ниже.
При отсутствии сведений о теплотах образования или сгорания можно вычислить теплоту образования при 298 К методом Коттрелла по энергии связей. Но, поскольку в справочных таблицах приведены усредненные значения энергии связей, без учета конкретного влияния образующихся индивидуальных связей в соединении, то результат расчета может существенно отличаться от экспериментальных данных.
Значения теплот образования могут быть рассчитаны также при использовании теплового эффекта реакции, вычисляемого из равновесных данных по уравнению Гиббса-Гельмгольца [4, 13].
Для вычисления ΔS0298, iжидких элементорганических соединений основным исходным параметром является температура плавления в виду того, что для рассматриваемого соединения определить эту величину не представляется возможной, определение энтропии производится полуэмпирическими зависимостями [4, 26].
2.2 Расчет термодинамических характеристик основной реакции
В данной работе предлагается использовать борат метилфосфит в качестве ингибитора коррозии в нейтральных средах, получаемого по схеме [24]:

Для расчета термодинамических параметров процесса необходимо знать зависимость теплоемкости от температуры для каждого соединения вида:
Cp = f(t) = Δa + Δb T + Δc`/T2 + ΔcT2, (4)
где a, b, c, c`- коэффициенты (табличные значения для Н3ВО3 и С2Н7РО3), а также значения H298, S298 .
Поскольку значения указанных величин для целевого продуктачастично неизвестны, рассчитаем их, используя методы, рассмотренные в разделе 2.1.1.
Получим зависимость теплоемкости от температуры, используя метод Неймана - Коппа. В этом случае используется правило сложения теплоемкостей элементов, составляющих соединение:
Cp = ![]() ,
,
где cp– теплоемкость соединения, ср,i – теплоемкость составляющего его i – го элемента (с учетом количества атомов).
Таблица 2.1 – Исходные данные для расчета теплоемкости борат метилфосфита
| Элемент (вещество) | ср= f(T) | Литературный источник | ||
| а | b ·103 | c`·10-5 | ||
| Р | 16,961 | 14,901 | - | [17] |
| C | 17,17 | 4,27 | -8,79 | [16] |
| Н2 | 27,3 | 3,27 | 0,5 | [17] |
| O2 | 29,98 | 4,2 | -1,7 | [16] |
| В | 16,056 | 10,01 | -6,28 | [15] |
Δa = ![]() ;
;
Δa =16,961·3 + 17,17·2 + 27,3·5,5 + 29,98· 5,5 + 16,056·2 = 432,375
остальные коэффициенты ряда рассчитываются аналогично:
Δb = 114,338·10-3
Δc` = –36,74·105
cp= 432,375 + 114,338·10-3·Т – 36,74·105/Т2
Определение зависимости теплоемкости от температуры были произведены экспериментальным путем.
Чтобы сравнить значения теплоемкости, рассчитанные с помощью рассмотренного метода, и полученные экспериментально [24], представим результаты расчетов, выполненных аналогично рассмотренным, в виде таблицы, а затем построим графики зависимости теплоемкости от температуры.
Таблица 2.2 – Результаты расчета изобарной теплоемкости
| Температура Т,К | Расчет по методу Неймана-Коппа Ср, Дж/(моль·К) | Экспериментальное определение Ср, Дж/(моль·К) |
| 353 | 443,26 | 430,32 |
| 363 | 446,00 | 435,15 |
| 373 | 448,62 | 442,45 |
| 383 | 451,12 | 448,59 |
| 393 | 453,53 | 456,87 |
| 403 | 455,84 | 459,25 |
| 413 | 458,06 | 462,37 |
| 423 | 460,21 | 464,01 |
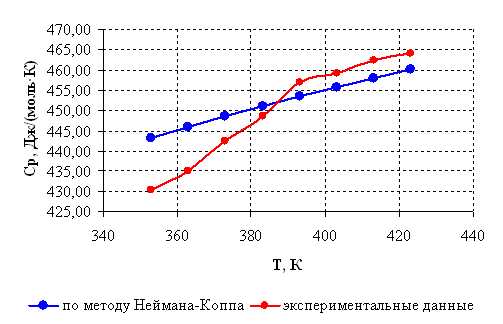
Рисунок 2.1 – Зависимость теплоемкости борат метилфосфита от температуры.
Как видно из графиков (рисунок 2.1) , рассчитанная по методу Неймана-Коппа теплоемкость несколько различается, однако максимальная разница между значениями не превышает допустимых 8 % [18] (для температуры 353 К, где разница максимальна, она составляет 3,1 % по отношению к меньшему значению теплоемкости).
Таким образом, доказана возможность использования вышеприведенного метода для дальнейших расчетов в рассматриваемом интервале температур.
Получим зависимости энтальпии и энтропии вида:
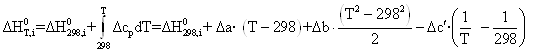
![]()
![]()
![]()
Согласно [11] ![]() = –4049,34 кДж/моль (вычислено по энергиям связей), таким образом, задача сводится к определению ΔS0298, i.
= –4049,34 кДж/моль (вычислено по энергиям связей), таким образом, задача сводится к определению ΔS0298, i.
Как было сказано выше все эмпирические методы расчета энтропии жидких веществ не подходят для данного соединения, поэтому воспользуемся полуэмпирической зависимостью [18]:
![]()
Определим основные термодинамические параметры основной реакции. Данные для термодинамического расчета реакции синтеза представлены в таблице 2.3.
Таблица 2.3 – Термодинамические данные веществ участников реакции
| Вещество | ср = f(T) | ΔН0 298, кДж/моль | ΔS0298 Дж/К·моль | |||
| a | b ·103 | c`·10-5 | с·106 | |||
| H3BO3 | 81,39 | – | – | – | -1094,89 | 88,8 |
| C2H7PO3 | 79,39 | 21,62 | -19,21 | – | -784,14 | 67,70 |
| Борат метилфосфит | 432,375 | 114,348 | -36,74 | – | -4049,34 | 595,11 |
| СН3ОН | 15,29 | 105,269 | – | -31,07 | -79,634 | 57,29 |
| Итого | 92,59 | 470,56 | 20,90 | -31,07 | 174,32 | 443,57 |
Зависимости энтальпии и энтропии реакции от температуры:
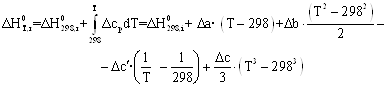
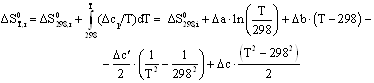
![]()
![]()
Руководствуясь ранее приведенным порядком расчета подобных зависимостей, получим:

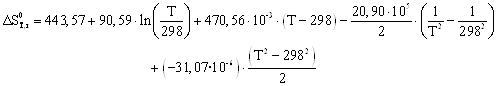
Результаты вычислений представлены в таблице 2.4.
Таблица 2.4 – Результаты расчета термодинамических параметров
| Температура, К |
Дж/моль | ΔST,r, Дж/моль·К | ΔGт, r, Дж/моль | ln Кр | Kр |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 353 | 188751,92 | 487,96 | 16501,11 | -5,62 | 0,0036 |
| 363 | 191485,71 | 495,60 | 11583,21 | -3,84 | 0,0215 |
| 373 | 194255,56 | 503,13 | 6589,50 | -2,12 | 0,1194 |
| 383 | 197062,08 | 510,55 | 1521,03 | -0,48 | 0,6202 |
| 393 | 199905,84 | 517,88 | -3621,21 | 1,11 | 3,0292 |
| 403 | 202787,32 | 525,12 | -8836,29 | 2,64 | 13,9750 |
| 413 | 205706,96 | 532,28 | -14123,34 | 4,11 | 61,1406 |
| 423 | 208665,15 | 539,35 | -19481,56 | 5,54 | 254,5595 |
По результатам вышеприведенных расчетов построим графики соответствующих зависимостей.
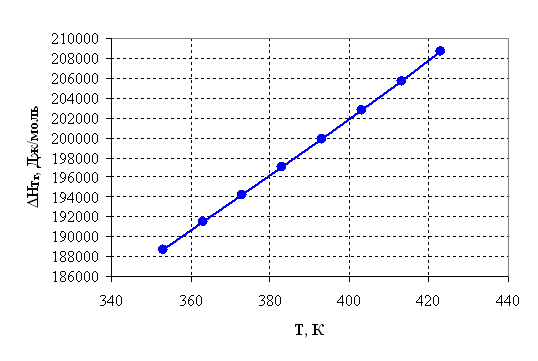
Рисунок 2.2 – Зависимость энтальпии от температуры.
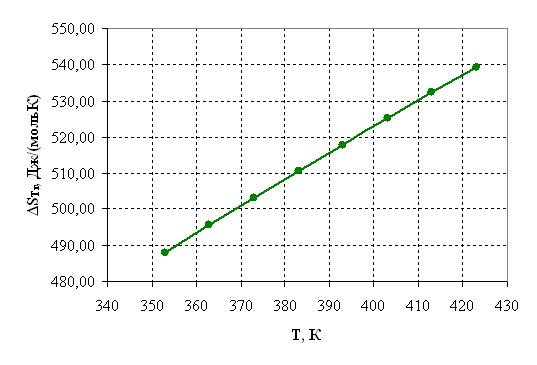
Рисунок 2.3 – Зависимость энтропии от температуры.
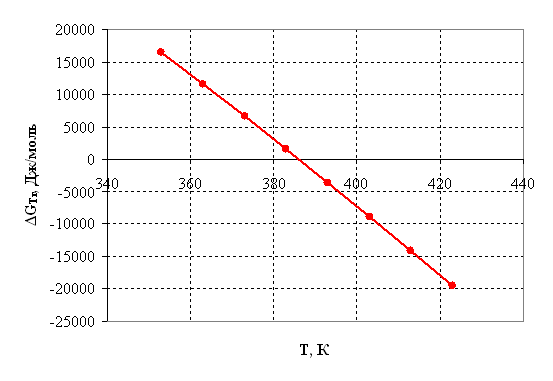
Рисунок 2.4 – Зависимость энергии Гиббса от температуры.
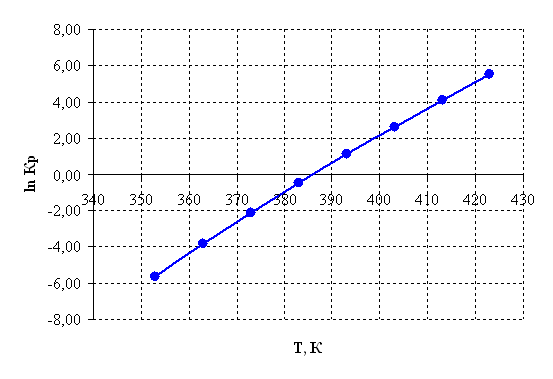
Рисунок 2.5 – Зависимость логарифма константы равновесия от температуры.
По приведенным результатам расчета термодинамических характеристик рассматриваемой реакции можно сделать следующие выводы:
1) Так как ![]() >0, то реакция эндотермическая
>0, то реакция эндотермическая
2) Энергия Гиббса становится отрицательной при температуре 385 К, следовательно, процесс термодинамически возможен, только при условие, что температура реакции больше 385 К, далее видно, что с повышением температуры, термодинамическая вероятность протекания процесса в прямом направлении линейно возрастает. На практике процесс осуществляется при 390 – 400 К.
3) При температурах больше 385 К константа равновесия Кр >1 и далее с повышением температуры экспоненциально возрастает, тем самым равновесие смещается в сторону продуктов реакции.
Похожие работы
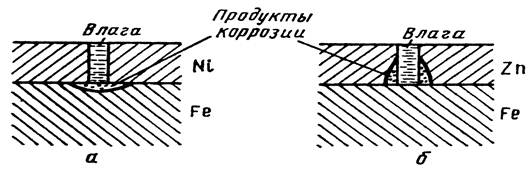
... составов, застойные воды и некоторые органические продукты. Электрохимическая коррозия подчиняется законам электрохимической кинетики. Скорость ее можно определить на основе законов Фарадея. Электрохимическая коррозия встречается чаще всего и наиболее опасна для металлов. Она может протекать в газовой атмосфере, когда на поверхности металла возможна конденсация влаги (атмосферная коррозия), в ...
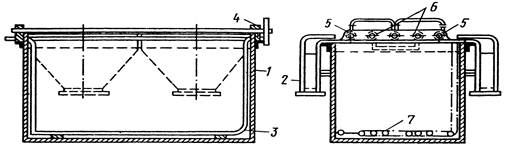
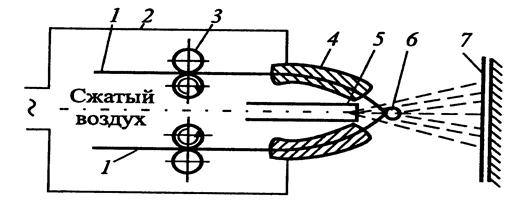
... и их содержимым. Способ изящен, и его применение, по-видимому, будет расширяться, как только будут преодолены сложности измерения и контроля. Покрытия, как метод защиты металлов от коррозии. Защита металлов, основанная на изменение их свойств, осуществляется или специальной обработкой их поверхности, или легированием. Обработка поверхности металла с целью уменьшения коррозии проводится одним ...
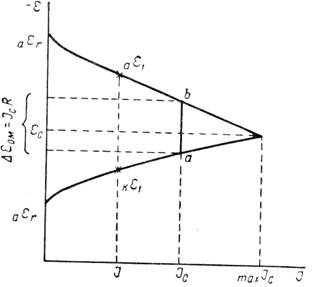
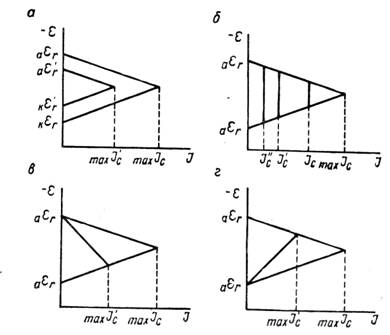
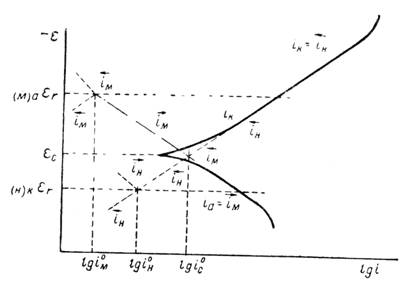
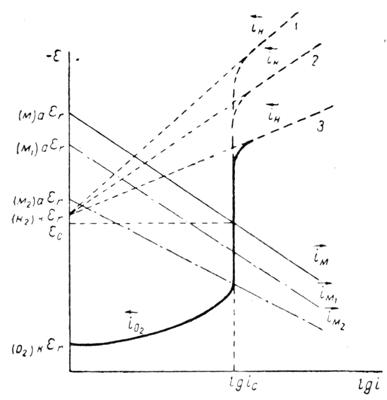
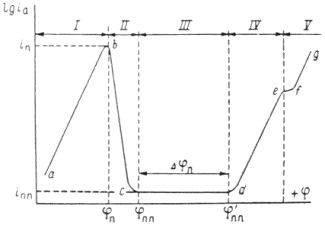
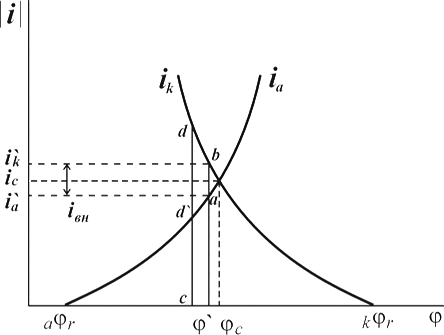
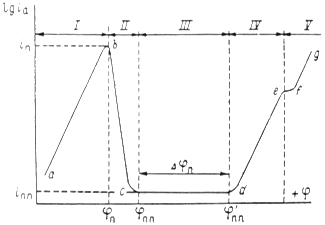
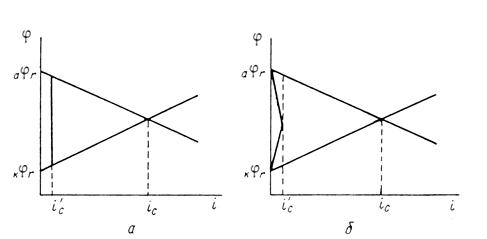
... Основным критерием, характеризующим состояние поверхности металла, является электродный потенциал. Обычно возможность применения анодной защиты для конкретного металла или сплава определяют методом снятия анодных поляризационных кривых. При этом получают следующие данные: а) потенциал коррозии металла в исследуемом растворе; б) протяженность области устойчивой пассивности; в) плотность тока в ...
... обратимых потенциалов кислородного электрода при различных рН среды и Р P (атм) V ,B, при рН среды рН=0 рН=7 рН=14 0,21 +1,218 +0,805 +0,381 1 +1,229 +0,815 +0,400 Коррозия металла с кислородной деполяризацией в большинстве практических случаев происходит в электролитах, соприкасающихся с атмосферой, парциальное давление кислорода в которой ...


0 комментариев