Навигация
Пусть основной период данной функции равен Т. Тогда для данной функции при любых действительных х рассмотрим равенство
A sin (m (x + T) + ![]() ) = A sin (mx +
) = A sin (mx + ![]() ).
).
Следовательно,
A (sin (m (x + T) + ![]() ) – sin (mx +
) – sin (mx + ![]() ) = 0.
) = 0.
Применяя формулу разности синусов, будем иметь:
2А sin![]() cos
cos ![]() = 0
= 0
2А sin![]() cos
cos ![]() = 0
= 0
2А sin![]() cos
cos ![]() = 0
= 0
2А sin![]() cos
cos![]() = 0
= 0
Это произведение должно равняться нулю независимо от значений х.
Так как х - переменная величина, то 2cos![]()
![]() 0, А
0, А![]() 0 по условию, тогда sin
0 по условию, тогда sin ![]() = 0, откуда следует
= 0, откуда следует
![]() =
= ![]() , или
, или ![]() , где n
, где n![]() Z.
Z.
Из множества значений Т наименьшее положительное значение получим при наименьшем положительном значении n = 1, значит период данной функции
![]() .
.
Заметим, что период функции у = А sin (mx + ![]() ) не зависит от A и
) не зависит от A и ![]() .
.
Аналогично можно найти основные периоды и остальных тригонометрических функций.
Таким образом, функции
y = sin x и y = cos x имеют основной период Т = 2![]()
у = tg x и у = ctg x имеют основной период Т = ![]() ,
,
а функции у = sin (mx + ![]() ) и у = cos(mx +
) и у = cos(mx + ![]() ) имеют основной период Т =
) имеют основной период Т = ![]() .
.
Функции у = tg (mx + ![]() ) и у = ctg (mx +
) и у = ctg (mx + ![]() ) имеют основной период Т =
) имеют основной период Т = ![]() .
.
![]() Отметим некоторые свойства периодических функций. Заметим, что сумма разность, произведение и частное двух периодических функций может быть функцией как периодической, так и не периодической.
Отметим некоторые свойства периодических функций. Заметим, что сумма разность, произведение и частное двух периодических функций может быть функцией как периодической, так и не периодической.
Теорема 1. Если периодические функции y = f1 (x) и y = f2 (x), x Î X, имеют один и тот же период T, то их сумма, разность, произведение тоже будут периодическими функциями и число Т будет их периодом.
Доказательство Так как функция y = f1 (x) – периодическая с периодом Т ¹ 0, то для любого x Î X выполняется равенство
f1 (x +Т) = f1 (x) (1)
Так как функция y = f2 (x) – периодическая с периодом Т ¹ 0, то для любого x Î X выполняется равенство
f2 (x +Т) = f2 (x) (2)
Рассмотрим функцию z (x) = f1 (x) ± f2 (x), заданную на множестве X. Тогда для любого x Î X согласно равенствам (1) и (2) будем иметь
z (x +T) = f1 (x +T) ± f2 (x +Т) = f1 (x) ± f2 (x) = Z (x).
Последнее равенство доказывает периодичность функции z (x) представляющей собой сумму или разность двух периодических функций с одним и тем же периодом Т.
Рассмотрим функцию t (x) = f1 (x)×f2 (x), заданную на множестве Х. Тогда для любого x Î X согласно равенствам (1) и (2) будем иметь
t (x +T) = f1 (x +T) ×f2 (x +Т) = f1 (x) ×f2 (x) = t (x).
Данное равенство доказывает периодичность функции t(x) представляющей собой произведение двух периодических функций с одним и тем же периодом Т, причем число Т является периодом как функции t(x), так и функции z(x).
Замечание. Если число Т было наименьшим положительным периодом (т.е. основным периодом) двух заданных функций, то после их сложения или умножения Т может перестать быть наименьшим из положительных периодов.
Пример 5. Функция f1 (x) = 3 sin x + 2 имеет основной период 2p, функция f2 (x) = 2 – 3 sin x имеет основной период 2p, а их сумма
z (x ) = f1 (x) +f2 (x) = 3 sin x + 2 + 2 – 3 sin x = 4
наименьшего положительного периода не имеет, так как при любом действительном значении a ¹ 0 z(x+a) = z(x), т.е. любое действительное число является периодом функции z(x), а наименьшего положительного среди действительных чисел нет.
Пример 6. Функция j1(x) = sin x +1 и j2(x) = 1- sin x имеют наименьший положительный период 2p, а для произведения
t(x) = j1(x) × j2(x) = (sin x +1)(1- sin x) = 1- sin2x = cos2x =![]()
наименьшим положительным периодом есть число p .
Определение Периоды функций Т1 и Т2 называются соизмеримыми, если существуют такие целые отличные от нуля числа m и n, что m×T1 = n×Т2.
Пример 7. Выясним, являются ли соизмеримыми периоды Т1 = ![]() и
и
Т2=![]()
Решение. Данные периоды будут соизмеримыми, если уравнение ![]() ×m =
×m = ![]() ×n имеет решение на множестве Z \ {0}. Умножим обе части данного уравнения на 6 (наименьшее общее кратное чисел 3 и 2), получим равносильное уравнение 4m = 15n, откуда m = 15k, n = 4k, где k Î Z \ {0}. Например, при k = 1 получим
×n имеет решение на множестве Z \ {0}. Умножим обе части данного уравнения на 6 (наименьшее общее кратное чисел 3 и 2), получим равносильное уравнение 4m = 15n, откуда m = 15k, n = 4k, где k Î Z \ {0}. Например, при k = 1 получим
![]() × 15 =
× 15 = ![]() ×4 = 10
×4 = 10
Ответ: Периоды Т1 и Т2 соизмеримы.
Теорема 2. Если периодические функции y = f1(x) и y = f2(x), x Î X, имеют соизмеримые периоды Т1 и Т2 то они имеют общий период.
Доказательство. Так как периоды Т2 и Т2 соизмеримы, то существуют целые отличные от нуля числа m и n такие, что m ×T1 = n × T2 = T ¹ 0. Следовательно, Т – общий период функций y = f1(x) и y = f2 (x). Теорема доказана.
Замечание. По теореме 1 число Т будет также периодом функций
z (x)= f1(x) ± f2 (x), t(x) = f1(x) f2 (x).
Пример 8. Найти период функции
f(x) = sin2x + 3sin(3x-2) - ![]() cos(
cos(![]() x +1).
x +1).
Решение. Так как период синуса равен 2p, функция sin2x имеет период ![]() = p функция sin(3x-2) = sin(3x-2 + 2p) = 3sin3(x-
= p функция sin(3x-2) = sin(3x-2 + 2p) = 3sin3(x-![]() +
+ ![]() ) и ее период равен
) и ее период равен ![]() . Аналогично, функция -
. Аналогично, функция -![]() cos(
cos(![]() x +1) имеет период
x +1) имеет период ![]() =
= ![]() p.
p.
Для того, чтобы найти общий период функции, представим периоды
Т1 = p; Т2 =![]() p и Т3 =
p и Т3 = ![]() p в другом виде, а именно, коэффициенты при p в полученных периодах приведем к общему знаменателю, получим
p в другом виде, а именно, коэффициенты при p в полученных периодах приведем к общему знаменателю, получим
Т1 = ![]() p = 6×
p = 6×![]() ; Т2 =
; Т2 = ![]() p = 4×
p = 4×![]() и Т3 =
и Т3 = ![]() p =
p = ![]() ×p и найдем наименьшее общее кратное числителей этих коэффициентов 6, 4 и 15. Оно равно 60. Следовательно, число Т = 60×
×p и найдем наименьшее общее кратное числителей этих коэффициентов 6, 4 и 15. Оно равно 60. Следовательно, число Т = 60×![]() = 10p – основной период данной функции.
= 10p – основной период данной функции.
Пример 9. Найти период функции y = cos5x-sin2x.
Решение. Функция y = cos5x имеет период T1 = ![]() ; функция y = sin2x – период Т2 =
; функция y = sin2x – период Т2 = ![]() = p. Представим периоды Т1 и Т2 в другом виде: Т1 = 2×
= p. Представим периоды Т1 и Т2 в другом виде: Т1 = 2×![]() ; Т2 = 5×
; Т2 = 5×![]() . Таким образом видно, что периоды Т1 и Т2 соизмеримы: 5Т1 = 2Т2, откуда 5×
. Таким образом видно, что периоды Т1 и Т2 соизмеримы: 5Т1 = 2Т2, откуда 5×![]() = 2×p = 2p. Следовательно, число 2p является периодом данной функции.
= 2×p = 2p. Следовательно, число 2p является периодом данной функции.
Пример 10. Найти основной период функции y = sin2x.
Решение. Понизим степень функции y = sin2x. Тогда y = ![]() =
=
![]() -
-![]() cos2x. Период этой функции равен периоду cos2x
cos2x. Период этой функции равен периоду cos2x ![]() = p. Таким образом основной период данной функции равен p.
= p. Таким образом основной период данной функции равен p.
Замечание. Если Т1 и Т2 – основные периоды функций f1(x) и f2(x), то наименьшее положительное число Т, удовлетворяющее условиям:
Т = mT1 = nT2, где m, n Î Z \ {0}, не обязательно является основным периодом функций f1(x) ± f2(x) и f1(x) × f2(x).
Например, основные периоды функций y = cos2x + sinx и y = -sinx равны 2p, а основной период их суммы y = cos2x равен p.
Или, вернемся к примеру 6 и посмотрим на функцию y = sin2x как на произведение функций y = sinx ×sinx. Основной период функции y = sinx есть число 2p, но решая пример 6, мы показали, что основной период функции
y = sin2x равен p.
Заметим, что сложная функция, промежуточным аргументом которой служит периодическая функция, есть функция периодическая, причем периоды этих функций совпадают. Докажем
Теорему 3. Если y = f(j(x)) – сложная функция, где j(x) – периодическая функция с периодом Т, то и сложная функция периодическая с периодом Т.
Доказательство. Так как j(x) – периодическая функция с периодом Т, то для любого действительного x из области определения функции j(x) имеем
j(x + Т) = j(x),
тогда для функции y = f(j(x)) при любом действительном х из области определения функции j(x) будем иметь
j(x + Т) = f (j(x)) = f(j(x)) = y(x).
Последнее равенство доказывает, что функция y = f(j(x)) периодическая с периодом Т.
Пример 11. Функция y = cos3x периодическая с периодом ![]() = p. В силу теоремы 3 функция y = 5cos22x +
= p. В силу теоремы 3 функция y = 5cos22x + ![]() +3 периодическая с периодом p.
+3 периодическая с периодом p.
Рассмотрим примеры на доказательство периодичности или не периодичности функций.
Пример 12. Доказать, что функция y = sin![]() не является периодической.
не является периодической.
Доказательство. I способ: D(y) = [0;+¥). Пусть положительное число
Т – период данной функции, тогда должно выполнятся условие (х-Т) Î D(y), для любого x Î D(y). Но при x = 0 (х-Т) Ï D(y), следовательно, T > 0 не является периодом функции.
Докажем, что Т < 0 не может быть периодом функции y = sin![]() .
.
Если T < 0 – период данной функции, то должно выполнятся условие (х + Т) Î D(y) для любого x Î D(y). Но при x = 0 (х + Т) Ï D(y), следовательно, T < 0 не является периодом функции.
II способ: Предположим, что функция y = sin![]() имеет период, равный Т. Тогда y = sin
имеет период, равный Т. Тогда y = sin![]() = y = sin
= y = sin![]() при любом действительном x Î D(y). При x = 0 будем иметь, что sin
при любом действительном x Î D(y). При x = 0 будем иметь, что sin![]() = sin 0 = 0. Значит
= sin 0 = 0. Значит
![]() = pn, (1)
= pn, (1)
а при x = T получим sin![]() = sin
= sin![]() = 0. Следовательно,
= 0. Следовательно,
sin![]() = pk. (2)
= pk. (2)
Разделив почленно (2) на (1) при n ¹ 0, получим ![]() =
= ![]() =
=![]() , чего не может быть, так как
, чего не может быть, так как ![]() число иррациональное.
число иррациональное.
Пример 13. Доказать, что функция y = cos2 x не является периодической.
Доказательство. Пусть данная функция имеет период Т ¹ 0. Тогда для любого x Î D(y) (D(y) = R) должно выполнятся равенство
cos (x+T)2 = cos x2 или
cos (x+T)2 - cos x2 = 0
Преобразуем данное равенство по формуле разности косинусов, получим
2 sin ![]() × sin
× sin ![]()
2sin (x2 + T×x + ![]() ) × sin (T×x +
) × sin (T×x + ![]() ) = o
) = o
Это произведение должно равняться нулю независимо от значений переменной величины x, а это невозможно, sin (T×x + ![]() ) ¹ o и
) ¹ o и
sin (x2 + T×x + ![]() ) ¹ 0. Значит допущение, что функция y = cos2 x периодическая неверно, т.е. данная функция не является периодической.
) ¹ 0. Значит допущение, что функция y = cos2 x периодическая неверно, т.е. данная функция не является периодической.
Пример 14. Доказать, что функция y = |sin (x)| является периодической с периодом p.
Доказательство. D(y) = R. Пусть периодом данной функции будет число Т ¹ 0. Тогда
|sin (x + Т)| = |sin (x)| (3)
Это равенство будет выполнятся в двух случаях:
1) sin (x + Т) = sin (x) и тогда
sin (x + Т)-sin (x) = 0
2 cos (x + ![]() )×sin
)×sin ![]() = 0.
= 0.
Это произведение должно равняться нулю независимо от переменной x, а это возможно только при sin ![]() = 0. Откуда
= 0. Откуда
![]() = pk и Т = 2pk, что приводит к основному периоду 2p.
= pk и Т = 2pk, что приводит к основному периоду 2p.
2) sin (x + Т) = -sin (x). (4)
Тогда sin (x + Т) +sin (x) = 0 и
2 sin (x + ![]() )×cos
)×cos ![]() = 0.
= 0.
Откуда ![]() =
= ![]() и Т = pn, что приводит к основному периоду Т = p. Так как при Т = p выполняется равенство (4), следовательно, и равенство (3). Значит, Т = p есть период функции y = |sin (x)|.
и Т = pn, что приводит к основному периоду Т = p. Так как при Т = p выполняется равенство (4), следовательно, и равенство (3). Значит, Т = p есть период функции y = |sin (x)|.
§5 Тестовые контрольные работы по теме «Числовые функции. Сложная функция. Четные нечетные функции. Периодические функции»
Рассмотрим комплект тестовых заданий по теме «Числовые функции. Сложная функция. Четные нечетные функции. Периодические функции».
При разработке данного комплекта тестовых заданий учитывались следующие моменты:
1) содержание заданий, вопросов охватывает наиболее принципиальные стороны и идеи темы;
2) в задания сделан акцент не на проверку навыков, а на выявление глубины освоения идейного содержания темы, проявлению математической эрудиции;
3) по усмотрению учителя тестовое задание может предлагаться ученикам не полностью, а частями.
4) задания обеспечивают возможность проведения итоговых занятий на заключительном этапе изучения понятия функции в школьном курсе математики.
Комплект тестовых заданий составлен в четырех вариантах и включает двенадцать вопросов. На каждый из них дается четыре ответа для выбора правильного из них. Вопросы в заданиях предлагаются в текстовой и графической формах. Задания рассчитаны на 45 минут работы школьника.
Вариант I
1. Какое равенство не задает функцию?
а) y2 = x2; б) y = x2; в) y = lg x; г) y = ![]() .
.
2. На каком из рисунков изображено множество точек координатной плоскости, которое нельзя рассматривать как график функции?
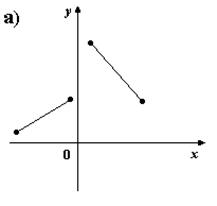
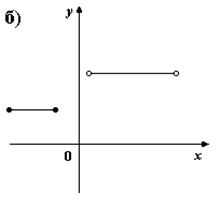
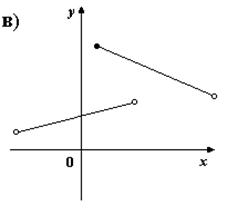
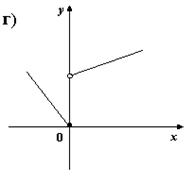
3) Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x)) ?
а) f(x) = tg(x), g(x) = arctg x; б) f(x) = ![]() , g(x) = x3;
, g(x) = x3;
в) f(x) = x2, g(x) = ![]() ; г) f(x) =
; г) f(x) = ![]() , g(x) = x2.
, g(x) = x2.
4) Даны функции f(x) = x2 и g(x) = ![]() . Какая запись в таком случае верна?
. Какая запись в таком случае верна?
а) f(g(x)) = (![]() )2; б) f(g(x)) =
)2; б) f(g(x)) = ![]() ;
;
в) f(g(x)) = |x|; г) f(g(x)) = x.
5) На каком из рисунков изображен график четной функции?
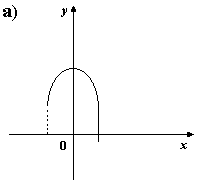

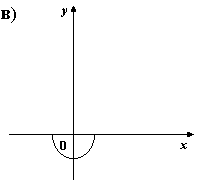
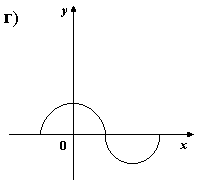
6. Укажите четную функцию.
а) y = sin (2x+1); б) y = sin (x2+1);
в) y = cos (x2+1); г) y = x+cos x.
7. Укажите нечетную функцию.
а) f(x) = x3 +1; б) f(x) = 2x – 2-x;
в) f(x) = 2x + 2-x; г) f(x) = ![]()
8. Какое высказывание ложно?
а) Сумма двух четных на R функций есть функция четная.
б) Разность двух четных на R функций есть функция четная.
в) Произведение двух четных на R функций есть функция четная.
г) Всякая функция есть функция четная, либо нечетная.
9. Какие из данных множеств могут быть областями определения периодических функций?
а) (-¥; +¥); б) (0;+¥); в) множество всех чисел, кроме чисел вида pk, где k = 0, ±1, ±2, …
10. Какая из функций обладает следующими свойствами:
существует такое t ¹ 0, что при любом x из области определения выполняется равенство f(x+t) = f(x)?
а) y = ![]() ; б) y = x2; в) y = sin
; б) y = x2; в) y = sin ![]() ; г) y = x sin x.
; г) y = x sin x.
11. Какая из функций не является периодической?
а) y = sin(x+1);
б) y = cos x + tg x;
в) y = x + sin x;
г) y = {x}.
12. Какая из функций имеет период ![]() ?
?
а) y = tg x – ctg x; б) y = sin 2x;
в) y = cos ![]() ; г) y = sin x + cos x.
; г) y = sin x + cos x.
Вариант II
1. Какое равенство задает отношение, при котором каждому значению x соответствует не более одного значения y?
а) y2 = x2; б) x2y2 = 1; в) ![]() = x; г) sin y = x.
= x; г) sin y = x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое нельзя рассматривать как график функции?
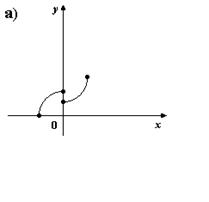
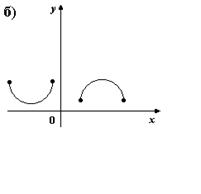
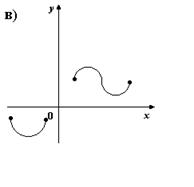
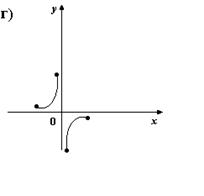
3. Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x))?
а) f(x) = sin x, g(x) = arcsin x; б) f(x) = arcsin x, g(x) = sin x;
в) f(x) = ex, g(x) = ln x; г) f(x) = ln x, g(x) = ex.
Даны функции f(x) = ![]() и g(x) = x2. Какая запись не верна?
и g(x) = x2. Какая запись не верна?
а) f(g(x)) = ![]() ; б)f(g(x)) =
; б)f(g(x)) = ![]() ;
;
в) f(g(x)) = ![]() ; г) f(g(x)) = (
; г) f(g(x)) = (![]() )2;
)2;
4. На каком из рисунков изображен график четной функции?
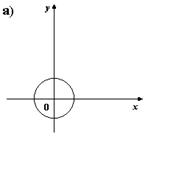
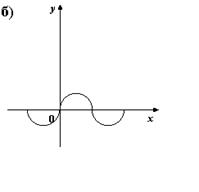

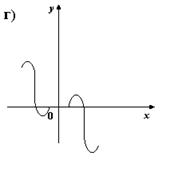
5. Укажите четную функцию.
а) y = x2 – x; б) y = 2x – 2-x;
в) 2x + 2-x; г) y = ![]() .
.
6. Укажите нечетную функцию.
а) f(x) = cos x + sin x; б) f(x) = sin x + tg x;
в) f(x) = cos x + sin x; г) f(x) = tg x×ctg x.
7. Какое высказывание ложно?
а) Сумма двух нечетных функций на R есть функция нечетная.
б) Разность двух нечетных функций на R есть функция нечетная.
в) Произведение двух нечетных функций на R есть функция нечетная.
г) Произведение трех нечетных функций на R есть функция нечетная.
8. Какие из данных множеств могут быть областями определения периодических функций?
а) R – множество действительных чисел;
б) (-2; +¥); в) R \ {2pk, k Î Z0}.
9. Какая из функций обладает следующим свойством:
существует такое t ¹ 0, что при любом x из области определения верно равенство f (x+t) = f(x)?
а) y = x3; б) y = ![]() ; в) y = x cos x; г) y = sin (
; в) y = x cos x; г) y = sin (![]() ).
).
10. Какая из функций не является периодической?
а) y = sin x + ctg x; б) y = cos (2x+1);
в) y = sin (![]() )2; г) y = sin x×tg x.
)2; г) y = sin x×tg x.
11. У какой функции наименьший положительный период больше 2p?
а) y = sin x + ![]() sin 2x +
sin 2x + ![]() sin 3x;
sin 3x;
б) y = 3 tg ![]() ;
;
в) y = tg x + ctg ![]() ;
;
г) y = sin2 x.
Вариант III
1. Какое равенство задает отношение, при котором некоторым значениям x соответствует более одного значения y?
а) y = arctg x; б) y = tg x; в) tg y = x; г) arctg y = x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое можно рассматривать как график функции?
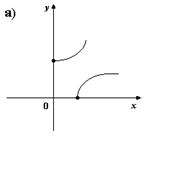
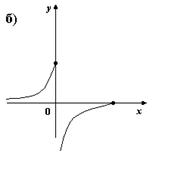
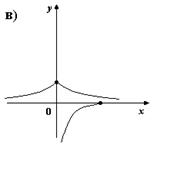
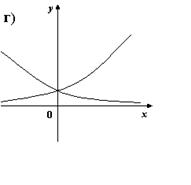
3. Для каких функций f и g равенство f(g(x)) = x верно не на всей области опреднления функции f(g(x))?
4.
а) f(x) = ![]() , g(x) =
, g(x) = ![]() ; б) f(x) = 2x, g(x) = 0,5x;
; б) f(x) = 2x, g(x) = 0,5x;
в) f(x) = arccos x, g(x) = cos x; г) f(x) = cos x, g(x) = arccos x.
5. Для каких функций f и g имеет место равенство f(g(x)) = g(f(x))?
6.
а) f(x) = ![]() , g(x) = x0; б) f(x) =
, g(x) = x0; б) f(x) = ![]() , g(x) = x4;
, g(x) = x4;
в) f(x) = ![]() , g(x) = x2; г) f(x) =
, g(x) = x2; г) f(x) = ![]() , g(x) = x3.
, g(x) = x3.
7. На каком из рисунков изображен график четной функции?
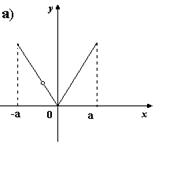
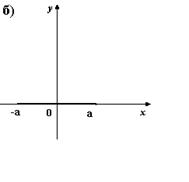
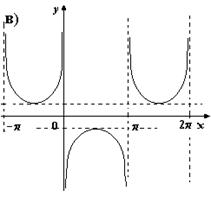

8. Укажите четную функцию.
9.
а) y = sin x + tg x; б) y = sin x×tg x;
в) y = cos x×ctg x; г) y = tg x + ctg x.
10. Укажите, какая из приведенных функций нечетная?
11.
а) f(x) = ![]() ; б) f(x) = lg
; б) f(x) = lg![]() ;
;
в) f(x) = 10x + 10-x; г) f(x) = x5 – 1.
12. Пусть f – четная функция на R, а g – нечетная функция на R. Какое утверждение истинно?
а) f + g – функция четная; б) f – g – фуункция нечетная;
в) f×g – функция нечетная; г) ![]() – функция четная.
– функция четная.
13. Какие из данных множеств могут быть областями определения периодических функций?
а) Q – множество рациональных чисел;
б) (-¥; 0);
в) множество интервалов вида (2pk, p(2k+1)), где k = 0, ±1; ±2…
14. Какая из периодических функций не имеет наименьшего положительного периода?
а) y = sin x; б) y = {x}; в) y = 5;
г) y = tg (80x + 3).
15. Какая из функций не является периодической?
а) y = sin ![]() ; б) y = tg x + sin 2x;
; б) y = tg x + sin 2x;
в) y = ![]() ; г) y = cos 4x.
; г) y = cos 4x.
16. Какие из следующих утверждений истинны?
а) Если число T – период функции f, то число 2T также период этой функции.
б) Если числа Т1 и Т2 – периоды функции f, то число (Т1+Т2) также период этой функции.
в) Если 2T – период функции f, то число T – также период этой функции.
г) Если T – период функции f, то число -T – также период этой функции.
Вариант IV
1. Какое равенство задает отношение, которое не является функцией?
а) ln y = x; б) arcsin y = x; в) sin y = sin x; г) ey = arcsin x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое можно рассматривать как график функции?
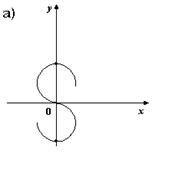
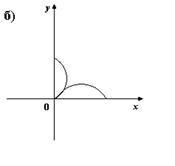
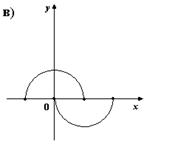
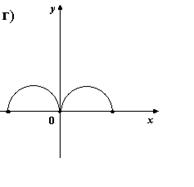
3. Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x))?
а) f(x) = tg x, g(x) = arctg x; б) f(x) = arctg x, g(x) = tg x;
в) f(x) = 3x + 2, g(x) = ![]() x -
x -![]() ; г) f(x) = - x, g(x) = - x.
; г) f(x) = - x, g(x) = - x.
4. Для каких функций f и g имеет место равенство f(g(x)) = g(f(x))?
а) f(x) = ![]() , g(x) =
, g(x) = ![]() ; б) f(x) = 10x, g(x) = lg x;
; б) f(x) = 10x, g(x) = lg x;
в) f(x) = x2, g(x) = x3; г) f(x) = x4, g(x) = ![]()
5. На каком из рисунков изображен график четной функции?
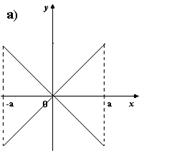
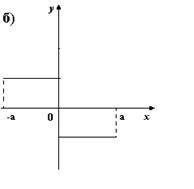
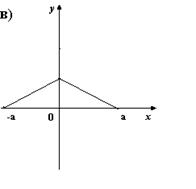
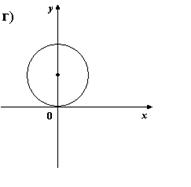
6. Укажите четную функцию.
7.
а) y = sin (![]() - x); б) y = 1 – sin x;
- x); б) y = 1 – sin x;
в) y = cos x + x3; в) y = (x + 4)2
8. Какая из приведенных функций нечетная?
а) f(x) = x sin x; б) f(x) = x + sin x;
в) f(x) = ctg2 x; г) f(x) = cos (![]() - x) + 2.
- x) + 2.
9. На какой вопрос следует дать отрицательный ответ?
а) Может ли четная функция быть периодической?
б) Может ли периодическая функция иметь лишь один нуль?
в) Верно ли, что произведение двух функций различной четности есть функция нечетная?
10. Какие из данных множеств могут быть областями определения периодических функций?
а) N – множество натуральных чисел;
б) [-p; p];
в) множество всех чисел, кроме числа вида ![]() (2k + 1),
(2k + 1),
где k = 0; ±1; ±2, …
Похожие работы
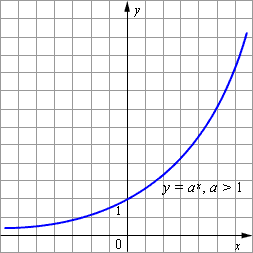
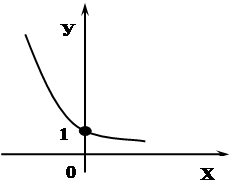
... детальный разбор этого материала при активной работе учащихся. Тщательно рассматриваются все определения, прорешиваются примеры – идет усвоение нового материала. 2.2 Методика введения показательной функции Изучение темы «Показательная функция» в курсе алгебры и начала анализа предусматривает знакомство учащихся с вопросами: Обобщение понятия о степени; понятие о степени с иррациональным ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...
... движение. Глава 3. развитие понятия функции в школьном курсе физике. §3.1. Функция как важнейшее звено межпредметных связей. В общей системе теоретических знаний учащихся по физике и математике в средней школе большое место занимает понятие «функция». Оно имеет познавательное и мировоззренческое значение и играет важную роль в реализации межпредметных связей [13]. Функция является одним ...



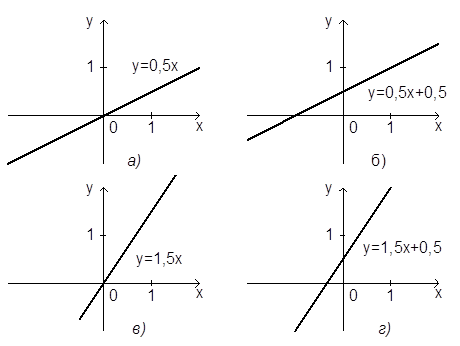
0 комментариев