Навигация
Какая из функций обладает следующим свойством: существует такое t ¹ 0, что при любом x из области определения верно равенство
11. Какая из функций обладает следующим свойством: существует такое t ¹ 0, что при любом x из области определения верно равенство
f(x) = f(x - t)?
а) y = 2 cos |x|; б) y = 3 + sin (2 + ![]() );
);
в) y = ![]() ; в) y = 2x×cos x.
; в) y = 2x×cos x.
12. Какая из функций не является периодической?
13.
а) y = |cos 2x|; б) y = sin x×cos ![]() ;
;
в) y = ![]() sin (6x +
sin (6x + ![]() ); г) y = 4 – cos (
); г) y = 4 – cos (![]() + x).
+ x).
14. У какой функции наименьший положительный период меньше ![]() ?
?
а) y = ![]() ; б) y = 3 cos
; б) y = 3 cos ![]() x;
x;
в) y = 2 sin (6x + ![]() ); г) y = -3 tg (
); г) y = -3 tg (![]() -
- ![]() ).
).
Таблица кодов ответов
| Номер варианта | Вопросы | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Ответы | ||||||||||||
| I | а | в | г | а | в | б | б | г | а, в | в | в | а |
| II | в | а | б | а | в | в | б | в | а, в | г | в | б |
| III | в | б | в | г | б | б | б | в | а, в | в | б | а, б, г |
| IV | г | г | б | в | в | а | б | б | в | а | б | в |
Заключение
Понятие функции является центральным в математическом образовании. От того, насколько полно и всесторонне школьник усвоит это понятие, зависит его дальнейшая адаптация в математической деятельности.
В школьном курсе математики учащиеся знакомятся с определением функции и той базы понятий, на котором оно основано, на протяжении всего периода обучения. При этом все содержание обучения построено так, что конечным результатом в идеале должно быть сформировано с одной стороны ясное и четкое представление об этом понятии, а с другой стороны близкое к современному пониманию функции как некоторого отображения произвольных множеств.
В данной работе сделана попытка, опираясь на основные школьные учебники, собрать материал по данной теме, систематизировать его для того, чтобы выделить важные моменты при формировании понятия функции и препятствовать формальному усвоению понятий, сопутствующих определению функции. Большую роль в достижении этой цели играют разработанные тестовые задания, разбор типичных примеров, в которых учащиеся зачастую дают неправильные ответы.
Данная работа охватывает весь материал, связанный с понятием функции в школьном курсе и может быть использована при работе на уроках в обычных, профильных классах и на факультативных занятиях по математике.
Литература
1. Ананченко К.О., Воробьев Н.Т., Петровский Г.Н. Алгебра. Учебник для 9 класса общеобразовательных школ с углубленным изучением математики. Минск: «Народная асвета», 1995.
2. Ананченко К.О., Коваленко В.С., Воробьев Н.Т. и др. Алгебра и начала анализа. Учебник для 10 класса с углубленным изучением математики общеобразовательной школы с русским языком обучения. Минск: «Народная асвета», 2000.
3. Вирченко Н.А., Ляшко И.И., Швецов К.И., Графики функций. Справочник. Киев: «Наукова думка», 1979.
4. Груденов Я.И. Изучение определений, аксиом, теорем. Пособие для учителей. М.: Прсвещение, 1981.
5. Кузнецова Е.П., Муравьева Л.Б., Шнеперман Л.Б., Ящин Б.Ю. Дидактические материалы по алгебре и началам анализа. 10 класс. Минск: «Народная асвета», 2000.
6. Майер Р.А. Из опыта изучения функций и пределов в старших классах. М.: Просвещение, 1981.
7. Майер Р.А. Задачи по формированию функциональных понятий.
8. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра. Учебник для 7 класса общеобразовательных учреждений. М.: Просвещение, 1997.
9. Никольская И.А., Тараканова З.П. Задания для программированного опроса по алгебре и началам анализа. М.: Высшая школа, 1981.
10. Потапов М.К., Александров В.В., Пасиченко П.И. Изд. отдел УНЦ ДО МГУ, 1995.
11. Саранцев Г.И. Формирование математических понятий в средней школе // Матем. В школе. 1998. № 6. С.27.
12. Семенович А.Ф. Об определении понятия «отображение» // Матем. В школе. 2000. № 5. С.35.
13. Столяр А.А. Педагогика математики. Минск: « Вышейшая школа», 1986.
14. Фройденталь Г.Ф. Математика как педагогическая задача. В двух частях. М.: Прсвещение, 1983.
Похожие работы
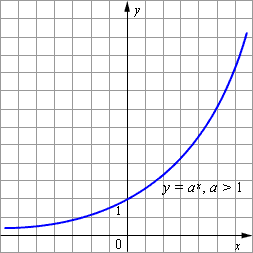
... детальный разбор этого материала при активной работе учащихся. Тщательно рассматриваются все определения, прорешиваются примеры – идет усвоение нового материала. 2.2 Методика введения показательной функции Изучение темы «Показательная функция» в курсе алгебры и начала анализа предусматривает знакомство учащихся с вопросами: Обобщение понятия о степени; понятие о степени с иррациональным ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...
... движение. Глава 3. развитие понятия функции в школьном курсе физике. §3.1. Функция как важнейшее звено межпредметных связей. В общей системе теоретических знаний учащихся по физике и математике в средней школе большое место занимает понятие «функция». Оно имеет познавательное и мировоззренческое значение и играет важную роль в реализации межпредметных связей [13]. Функция является одним ...



0 комментариев