Задания для самостоятельной работы

2. Задания для самостоятельной работы.

2.1. Три завода выпускают четыре вида продукции. Необходимо: а) найти матрицу выпуска продукции за квартал, если заданы матрицы помесячных выпусков А_1, А₂, А₃; б) найти матрицы приростов выпуска продукции за каждый месяц В₁ и В₂ и проанализировать результаты:

; ; .

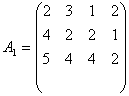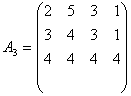2.2. Предприятие производит мебель трёх видов и продаёт её в четырёх регионах. Матрица 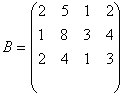 задаёт цену реализации единицы мебели i-го типа в j-м регионе. Определить выручку предприятия в каждом регионе, если реализация мебели за месяц задана матрицей .

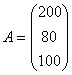2.3. По условию задачи 2 определить:1) полные затраты ресурсов 3-х видов на производство месячной продукции, если заданы нормы затрат матрицей 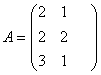и объём выпуска каждого из двух типов продукции ;

2) стоимость всех затраченных ресурсов, если задана стоимость единиц каждого ресурса .

2.4. В ремонтную мастерскую поступают телефонные аппараты, 70 % которых требуют малого ремонта, 20 % - среднего ремонта, 10% - сложного ремонта. Статистически установлено, что 10% аппаратов прошедших малый ремонт, через год требуют малого ремонта, 60% - среднего, 30% -сложного ремонта. Из аппаратов, прошедших средний ремонт, 20% требуют через год малого ремонта, 50% - среднего, 30% - сложного ремонта. Из аппаратов, прошедших сложный ремонт, через год 60% требуют малого ремонта, 40% - среднего. Найти доли из отремонтированных в начале года аппаратов, которые будут требовать ремонта того или иного вида: через 1 год; 2 года;3 года.

Практическое занятие.

Тема. Методы математического анализа для построения моделей СЭП.

Цель. Решение экономических задач с элементами моделирования, в которых применяются методы математического анализа.

1. Справочный материал.

 Функции находят широкое применение в экономической теории и практике. Спектр используемых в экономике функций весьма широк: от простейших линейных до функций, получаемых по определённому алгоритму с помощью рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени.

Наиболее часто используемые в экономике следующие функции:

1.  Функция полезности (функция предпочтения) – зависимость результата, эффекта некоторого действия от уровня (интенсивности) этого действия.

2.  Производственная функция – зависимость результата производственной деятельности от обусловивших его факторов.

3.  Функция выпуска – зависимость объёма производства от наличия или потребления ресурсов.

4.  Функция издержек – зависимость издержек производства от объёма продукции.

5.  Функции спроса, потребления и предложения – зависимость объёма спроса, потребления или предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.).

Учитывая, что экономические явления и процессы обуславливаются действием различных факторов, для их исследований широко используются функции нескольких переменных. Среди этих функций выделяют мультипликативные функции, позволяющие представить зависимую переменную в виде произведения факторных переменных, обращающих его в нуль при отсутствии действия хотя бы одного фактора.

Используются также сепарабельные функции, которые дают возможность выделить влияние различных факторов переменных на зависимую переменную, и в частности, аддитивные функции, представляющие одну и ту же зависимую переменную как при суммарном, но раздельном воздействии нескольких факторов, так и при одновременном их воздействии.

Кроме геометрического и механического существует ещё и экономический смысл производной. Во-первых, производная объема произведенной продукции по времени есть производительность труда в момент . Во-вторых, существует ещё одно понятие, характеризующее экономический смысл производной. Если издержки производства y рассматривать как функцию количества выпускаемой продукции x, - прирост продукции, - приращение издержек производства, а  - среднее приращение издержек производства на единицу продукции, тогда производная равная  выражает предельные издержки производства и характеризует приближённо дополнительные затраты на производство единицы дополнительной продукции.

Предельные издержки зависят от уровня производства (количества выпускаемой продукции) x и определяются не постоянными производственными затратами, а лишь переменными (на сырьё, топливо ит.п.). Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность и др.предельные величины.

Предельные величины характеризуют не состояние, а процесс, то есть изменение экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Следует учесть, что экономика не всегда позволяет использовать предельные величины в силу неделимости многих объектов экономических расчётов и прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных ит.д.). Вместе с тем в ряде случаев можно отвлечься от дискретности показателей и эффективно предельные величины.

Для исследования экономических процессов и решения прикладных задач часто используется понятие эластичности функции.

Эластичностью функции называется предел отношения относительного приращения функции y к относительному приращению переменной x при :

. (1)

Эластичность функции показывает приближённо, на сколько процентов изменится функция y=f(x) при изменении независимой переменной x на 1%. Это мера реагирования одной переменной величины на изменение другой.

Отметим свойства эластичности функции.

1. Эластичность функции равна произведению независимой переменной x на темп изменения функции , т.е. .

2. Эластичность произведения (частного) двух функций равна сумме (разности) эластичностей этих функций: , .

Эластичность функций применяется при анализе спроса и потребления. Например, эластичность спроса y относительно цены x – коэффициент, определяемый по формуле (1) и показывающий приближённо, на сколько процентов изменится спрос (объем потребления) при изменении цены (или дохода) на 1%.

Если эластичность спроса (по абсолютной величине) , то спрос считают эластичным, если - нейтральным, если  - неэластичным относительно цены (или дохода).

В практической деятельности часто приходится сталкиваться с такими задачам, которые рационально решать методами математического анализа. Это задачи на нахождение объёма продукции при известном значении прибыли, определении уровня потребления товаров при известном доходе, определение момента времени рентабельности производства, определение размеров вклада при известных начальных вложениях и т.п.

Задача 1. Издержки y (в руб.) на изготовление партии деталей определяются по формуле , где  - объём партии. Для первого варианта технологического процесса . Для второго варианта известно, что (руб.) при (дет.) и (руб.) при  (дет.). Провести оценку двух вариантов технологического процесса и найти себестоимость продукции для обоих вариантов при (дет.)

Решение.

Для второго варианта определяем параметры и из системы уравнений:

 откуда  и , т.е. .

Точка (х₀,y₀) пересечения двух прямых находится из системы их уравнений:

 откуда , .Очевидно, при объёме партии  выгоднее второй вариант технологического процесса, при  - первый вариант. Себестоимость продукции (руб.) при по первому варианту составляет , а по второму - .

Задача 2. Постоянные издержки  составляют 125 тыс.руб. в месяц, а переменные издержки - 700 руб. за каждую единицу продукции. Цена единицы продукции 1200 руб. Найти объём продукции , при котором прибыль равна: а) нулю (точка безубыточности); б) 105 тыс.руб. в месяц.

Решение:

а) Издержки производства  единиц продукции составят: (тыс.руб.). Совокупный доход (выручка) от реализации этой продукции , а прибыль (тыс.руб.). Точка безубыточности, в которой , равна (ед.).

б) Прибыль (тыс.руб.), т.е.  при (ед.).

Задача 3. Продолжительность выполнения  (мин.) при повторных операциях связана с числом  этих операций зависимостью . Вычислить, сколько минут выполняется работа при 50 операциях, если известно, что при , а при .

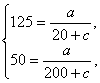Решение. Найдём параметры и , учитывая, что , . Получаем систему:  решая которую найдём , .

Итак,  при , (мин.)

Задача 4. Объём продукции u, произведённый бригадой рабочих, может быть описан уравнением (ед.), , где t – рабочее время в часах. Вычислить производительность труда, скорость и темп её изменения через час после начала работы и за час до её окончания.

Решение. Производительность труда выражается производной  (ед./час), а скорость и темп изменения производительности – соответственно производной и логарифмической производной : (ед./ч²),

 (ед./ч).

В заданные моменты времени  и  соответственно имеем: z(t)=112,5 (ед./ч), z’(t)=-20(ед./ч²), T_z(7)=-0,24 (ед./ч).

Итак, к концу работы производительность труда существенно снижается; при этом изменение знака z’(t) и T_z(t) с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется её снижением в последние часы.

Задача 5. Опытным путём установлены функции спроса  и предложения , где q и s – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, p – цена товара.

Найти: а) равновесную цену, т.е.цену при которой спрос равен предложению;

б) эластичность спроса и предложения для этой цены;

в) изменение дохода при увеличении цены на 5% от равновесной.

Решение. а) Равновесная цена находится из условия q=s, тогда , откуда p=2, т.е равновесная цена 2 ден.ед.

б) Найдём эластичность по спросу и предложению по формуле (1)

.

; . Для равновесной цены p=2 имеем ; . Так как полученные значения эластичностей по абсолютной величине меньше 1, то и спрос и предложение данного товара при равновесной (рыночной) цене неэластичны относительно цены. Это означает, что изменение цены не приведёт к резкому изменению спроса и предложения. Так, при увеличении цены p на 1% спрос уменьшится на 0,3%, а предложение увеличится на 0,8%.

в) При увеличении цены p на 5% от равновесной спрос уменьшится на 5^.0,3=1,5%, следовательно, доход возрастёт на 3,5%.

Задача 6. Зависимость между издержками производства y и объёмом выпускаемой продукции x выражается функцией (ден.ед.). Определить средние и предельные издержки при объёме продукции 10 ед.

Решение. Функция средних издержек выражается соотношением ; при x=10 средние издержки (на единицу продукции) равны (ден. ед.). Функция предельных издержек выражается производной ; при x=10 предельные издержки составят  (ден.ед.). Итак, если средние издержки на производство единицы продукции составляют 45 ден.ед., то предельные издержки, т.е. дополнительные затраты на производство дополнительной единицы продукции при данном уровне производства (объёме выпускаемой продукции 10 ед.) , составляют 35 ден.ед.

Задача 7. Выяснить, чему равны предельные и средние полные затраты предприятия, если эластичность полных затрат равна 1?

Решение. Пусть полные затраты предприятия y выражаются функцией , где x – объём выпускаемой продукции. Тогда средние затраты y₁ на производство единицы продукции . Эластичность частного двух функции равна разности их эластичностей, т.е. .

По условию , следовательно, . Это означает, что с изменением объёма продукции средние затраты на единицу продукции не меняются, т.е., откуда .

предельные издержки предприятия определяются производной . Итак,  т.е предельные издержки равны средним издержкам(полученное утверждение справедливо только для линейных функций издержек).